Scale-space axioms
Encyclopedia
In image processing
and computer vision
, a scale-space framework can be used to represent an image as a family of gradually smoothed images. This framework is very general and a variety of scale-space representations exist. A typical approach for choosing a particular type of scale-space representation is to establish a set of scale-space axioms, describing basic properties of the desired scale-space representation and often chosen so as to make the representation useful in practical applications. Once established, the axioms narrow the possible scale-space representations to a smaller class, typically with only a few free parameters.
A set of standard scale space axioms, discussed below, leads to the linear Gaussian scale-space, which is the most common type of scale space used in image processing and computer vision.
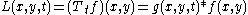of signal 
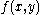obtained by smoothing with the Gaussian kernel 
satisfies a number of properties 'scale-space axioms' that make it a special form of multi-scale representation:
In fact, it can be shown that the Gaussian kernel is a unique choice given several different combinations of subsets of these scale-space axioms:
most of the axioms (linearity, shift-invariance, semigroup) correspond to scaling being a semigroup of shift-invariant linear operator, which is satisfied by a number of families integral transforms, while "non-creation of local extrema" is the crucial axiom which related scale-spaces to smoothing (formally, parabolic partial differential equation
s), and hence selects for the Gaussian.
The Gaussian kernel is also separable in Cartesian coordinates, i.e.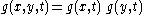
. Separability is, however, not counted as a scale-space axiom, since it is a coordinate dependent property related to issues of implementation. In addition, the requirement of separability in combination with rotational symmetry per se fixates the smoothing kernel to be a Gaussian.
In the computer vision
, image processing
and signal processing
literature there are many other multi-scale approaches, using wavelets and a variety of other kernels, that do not exploit or require the same requirements as scale-space descriptions do; please see the article on related multi-scale approaches
. There has also been work on discrete scale-space concepts that carry the scale-space properties over to the discrete domain; see the article on scale-space implementation for examples and references.
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
and computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, a scale-space framework can be used to represent an image as a family of gradually smoothed images. This framework is very general and a variety of scale-space representations exist. A typical approach for choosing a particular type of scale-space representation is to establish a set of scale-space axioms, describing basic properties of the desired scale-space representation and often chosen so as to make the representation useful in practical applications. Once established, the axioms narrow the possible scale-space representations to a smaller class, typically with only a few free parameters.
A set of standard scale space axioms, discussed below, leads to the linear Gaussian scale-space, which is the most common type of scale space used in image processing and computer vision.
Scale space axioms for the linear scale-space representation
The linear scale-space representation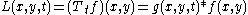 of signal 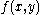obtained by smoothing with the Gaussian kernel satisfies a number of properties 'scale-space axioms' that make it a special form of multi-scale representation:- linearity
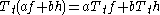
- shift invariance'
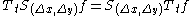
- the semi-group structure
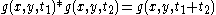
- existence of an infinitesimal generator
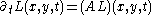
- non-creation of local extrema (zero-crossings) in one dimension,
- non-enhancement of local extrema in any number of dimensions
at spatial maxima and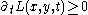 
at spatial minima, - rotational symmetry
for some function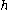 
, - scale invariance
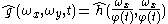
- positivity:
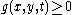, - normalization:
.
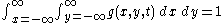where
and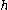 
are signals while 
and 
are constants,
where
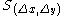denotes the shift (translation) operator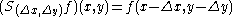 
with the associated cascade smoothing property
for some functions
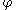and 
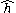where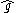 
denotes the Fourier transform of 
,
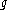In fact, it can be shown that the Gaussian kernel is a unique choice given several different combinations of subsets of these scale-space axioms:
most of the axioms (linearity, shift-invariance, semigroup) correspond to scaling being a semigroup of shift-invariant linear operator, which is satisfied by a number of families integral transforms, while "non-creation of local extrema" is the crucial axiom which related scale-spaces to smoothing (formally, parabolic partial differential equation
Parabolic partial differential equation
A parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
s), and hence selects for the Gaussian.
The Gaussian kernel is also separable in Cartesian coordinates, i.e.
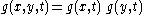. Separability is, however, not counted as a scale-space axiom, since it is a coordinate dependent property related to issues of implementation. In addition, the requirement of separability in combination with rotational symmetry per se fixates the smoothing kernel to be a Gaussian.In the computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
and signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
literature there are many other multi-scale approaches, using wavelets and a variety of other kernels, that do not exploit or require the same requirements as scale-space descriptions do; please see the article on related multi-scale approaches
Multi-scale approaches
The scale-space representation of a signal obtained by Gaussian smoothing satisfies a number of special properties, scale-space axioms, which make it into a special form of multi-scale representation. There are, however, also other types of multi-scale approaches in the areas of computer vision,...
. There has also been work on discrete scale-space concepts that carry the scale-space properties over to the discrete domain; see the article on scale-space implementation for examples and references.