Multibody system
Encyclopedia
A multibody system is used to model the dynamic behavior of interconnected rigid or flexible bodies, each of which may undergo large translational and rotational displacements.
. The simplest bodies or elements of a multibody system were already treated by Newton
(free particle) and Euler
(rigid body). Euler already introduced reaction forces between bodies. Later on, a series of formalisms have been derived, only to mention Lagrange
’s formalisms based on minimal coordinates and a second formulation that introduces constraints.
Basically, the motion of bodies is described by its kinematics
behavior. The dynamic
behavior results due to the equilibrium of applied forces and the rate of change in the momentum.
Nowadays, the term multibody system is related to a large number of engineering fields of research, especially in robotics and vehicle dynamics. As an important feature, multibody system formalisms usually offer an algorithmic, computer-aided way to model, analyze, simulate and optimize the arbitrary motion of possibly thousands of interconnected bodies.
The motion of the mechanism can be viewed in the following gif animation
There are two important terms in multibody systems: degree of freedom and
constraint condition.
OR
A minimum number of parameters required to define the position of an entity completely in a space is known as Degree of Freedom.
A rigid body has six degrees of freedom in the case of general spatial motion, three of them translational degrees of freedom and three rotational degrees of freedom. In the case of planar motion, a body has only three degrees of freedom with only one rotational and two translational degrees of freedom.
The degrees of freedom in planar motion can be easily demonstrated using e.g. a computer mouse. The degrees of freedom are: left-right, up-down and the rotation about the vertical axis.
implies a restriction in the kinematical degrees of freedom of one or more bodies. The classical constraint is usually an algebraic equation that defines the relative translation or rotation between two bodies. There are furthermore possibilities to constrain the relative velocity between two bodies or a body and the ground. This is for example the case of a rolling disc, where the point of the disc that contacts the ground has always zero relative velocity with respect to the ground. In the case that the velocity constraint condition cannot be integrated in time in order to form a position constraint, it is called non-holonomic. This is the case for the general rolling constraint. In addition to that there are non-classical constraints that might even introduce a new unknown coordinate, such as a sliding joint, where a point of a body is allowed to move along the surface of another body. In the case of contact, the constraint condition is based on inequalities and therefore such a constraint does not permanently restrict the degrees of freedom of bodies.
or Lagrange’s equations
.
The motion of rigid bodies is described by means of
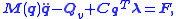(1)
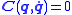(2)
This type of the equations of motion is based on so-called redundant coordinates, because the equations use more coordinates than degrees of freedom of the underlying system. The generalized coordinates are denoted by
, the mass matrix
is represented by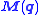
which may depend on the generalized coordinates.
represents the constraint conditions and the matrix 
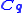(sometimes termed the Jacobian) is the derivation of the constraint conditions with respect to the coordinates. This matrix is used to apply constraint forces 
to the according equations of the bodies. The components of the vector 
are also denoted as Lagrange multipliers. In a rigid body, possible coordinates could be split into two parts,
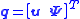
where
represents translations and 
describes the rotations.
is used to describe Coriolis and centrifugal terms in the equations of motion. The name is because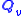 
includes quadratic terms of velocities and it results due to partial derivatives of the kinetic energy of the body.
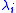is related to a constraint condition 
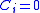and usually represents a force or a moment, which acts in “direction” of the constraint degree of freedom. The Lagrange multipliers do no "work" as compared to external forces that change the potential energy of a body.
Introduction
The systematical treatment of the dynamic behavior of interconnected bodies has led to a large number of important multibody formalisms in the field of mechanicsMechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
. The simplest bodies or elements of a multibody system were already treated by Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
(free particle) and Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
(rigid body). Euler already introduced reaction forces between bodies. Later on, a series of formalisms have been derived, only to mention Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
’s formalisms based on minimal coordinates and a second formulation that introduces constraints.
Basically, the motion of bodies is described by its kinematics
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
behavior. The dynamic
Analytical dynamics
In classical mechanics, analytical dynamics, or more briefly dynamics, is concerned about the relationship between motion of bodies and its causes, namely the forces acting on the bodies and the properties of the bodies...
behavior results due to the equilibrium of applied forces and the rate of change in the momentum.
Nowadays, the term multibody system is related to a large number of engineering fields of research, especially in robotics and vehicle dynamics. As an important feature, multibody system formalisms usually offer an algorithmic, computer-aided way to model, analyze, simulate and optimize the arbitrary motion of possibly thousands of interconnected bodies.
Applications
While single bodies or parts of a mechanical system are studied in detail with finite element methods, the behavior of the whole multibody system is usually studied with multibody system methods within the areas:- Physics enginePhysics engineA physics engine is computer software that provides an approximate simulation of certain physical systems, such as rigid body dynamics , soft body dynamics, and fluid dynamics, of use in the domains of computer graphics, video games and film. Their main uses are in video games , in which case the...
- RoboticsRoboticsRobotics is the branch of technology that deals with the design, construction, operation, structural disposition, manufacture and application of robots...
- Vehicle simulation (vehicle dynamicsVehicle dynamicsVehicle dynamics refers to the dynamics of vehicles, here assumed to be ground vehicles. Vehicle dynamics is a part of engineering primarily based on classical mechanics but it may also involve chemistry, solid state physics, electrical engineering, communications, psychology, control theory,...
, rapid prototypingRapid prototypingRapid prototyping is the automatic construction of physical objects using additive manufacturing technology. The first techniques for rapid prototyping became available in the late 1980s and were used to produce models and prototype parts. Today, they are used for a much wider range of applications...
of vehicles, improvement of stability, comfort optimization, improvement of efficiency, ...) - BiomechanicsBiomechanicsBiomechanics is the application of mechanical principles to biological systems, such as humans, animals, plants, organs, and cells. Perhaps one of the best definitions was provided by Herbert Hatze in 1974: "Biomechanics is the study of the structure and function of biological systems by means of...
- Aerospace engineeringAerospace engineeringAerospace engineering is the primary branch of engineering concerned with the design, construction and science of aircraft and spacecraft. It is divided into two major and overlapping branches: aeronautical engineering and astronautical engineering...
(helicopter, landing gears, behavior of machines under different gravity conditions) - Combustion engineCombustion engineCombustion engine may refer to:* Internal combustion engine* External combustion engine...
, gears and transmissions, chain driveChain driveChain drive is a way of transmitting mechanical power from one place to another. It is often used to convey power to the wheels of a vehicle, particularly bicycles and motorcycles...
, belt drive - HoistHoist (device)A hoist is a device used for lifting or lowering a load by means of a drum or lift-wheel around which rope or chain wraps. It may be manually operated, electrically or pneumatically driven and may use chain, fiber or wire rope as its lifting medium. The load is attached to the hoist by means of a...
, conveyor, paper millPaper millA paper mill is a factory devoted to making paper from vegetable fibres such as wood pulp, old rags and other ingredients using a Fourdrinier machine or other type of paper machine.- History :... - Particle simulation (granular media, sand, molecules)
- Dynamic simulationDynamic simulationDynamic simulation is the use of a computer program to model the time varying behavior of a system. The systems are typically described by ordinary differential equations or partial differential equations. As mathematical models incorporate real-world constraints, like gear backlash and rebound...
- Military applications
Example
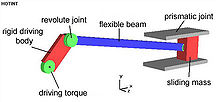
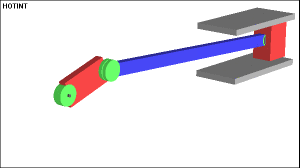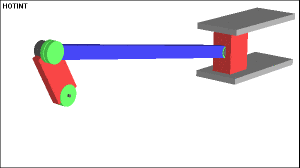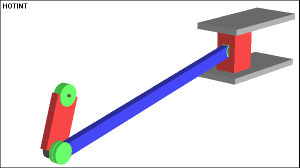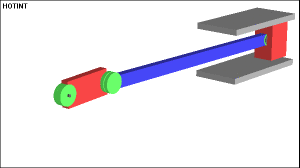
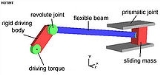
The following example shows a typical multibody system. It is usually denoted as slider-crank mechanism. The mechanism is used to transform rotational motion into translational motion by means of a rotating driving beam, a connection rod and a sliding body. In the present example, a flexible body is used for the connection rod. The sliding mass is not allowed to rotate and three revolute joints are used to connect the bodies. While each body has six degrees of freedom in space, the kinematical conditions lead to one degree of freedom for the whole system.
The motion of the mechanism can be viewed in the following gif animation
Concept
A body is usually considered to be a rigid or flexible part of a mechanical system (not to be confused with the human body). An example of a body is the arm of a robot, a wheel or axle in a car or the human forearm. A link is the connection of two or more bodies, or a body with the ground. The link is defined by certain (kinematical) constraints that restrict the relative motion of the bodies. Typical constraints are:- spherical joint; constrains relative displacements in one point, relative rotation is allowed; implies 3 kinematical constraints
- revolute jointRevolute jointA revolute joint is a one degree of freedom kinematic pair used in mechanisms. Revolute joints provide single-axis rotation function used in many places such as door hinges, folding mechanisms, and other uni-axial rotation devices. -See also:* Cylindrical joint* Kinematics* Degrees of freedom *...
; only one relative rotation is allowed; implies 5 kinematical constraints; see the example above - prismatic jointPrismatic jointA prismatic joint provides a linear sliding movement between two bodies, and is often called a slider, as in the slider-crank linkage. A prismatic joint is formed with a polygonal cross-section to resist rotation...
; relative displacement along one axis is allowed, constrains relative rotation; implies 5 kinematical constraints
There are two important terms in multibody systems: degree of freedom and
constraint condition.
Degree of freedom
The degrees of freedom denote the number of independent kinematical possibilities to move.OR
A minimum number of parameters required to define the position of an entity completely in a space is known as Degree of Freedom.
A rigid body has six degrees of freedom in the case of general spatial motion, three of them translational degrees of freedom and three rotational degrees of freedom. In the case of planar motion, a body has only three degrees of freedom with only one rotational and two translational degrees of freedom.
The degrees of freedom in planar motion can be easily demonstrated using e.g. a computer mouse. The degrees of freedom are: left-right, up-down and the rotation about the vertical axis.
Constraint condition
A constraint conditionConstraint algorithm
In mechanics, a constraint algorithm is a method for satisfying constraints for bodies that obey Newton's equations of motion. There are three basic approaches to satisfying such constraints: choosing novel unconstrained coordinates , introducing explicit constraint forces, and minimizing...
implies a restriction in the kinematical degrees of freedom of one or more bodies. The classical constraint is usually an algebraic equation that defines the relative translation or rotation between two bodies. There are furthermore possibilities to constrain the relative velocity between two bodies or a body and the ground. This is for example the case of a rolling disc, where the point of the disc that contacts the ground has always zero relative velocity with respect to the ground. In the case that the velocity constraint condition cannot be integrated in time in order to form a position constraint, it is called non-holonomic. This is the case for the general rolling constraint. In addition to that there are non-classical constraints that might even introduce a new unknown coordinate, such as a sliding joint, where a point of a body is allowed to move along the surface of another body. In the case of contact, the constraint condition is based on inequalities and therefore such a constraint does not permanently restrict the degrees of freedom of bodies.
Equations of motion
The equations of motion are used to describe the dynamic behavior of a multibody system. Each multibody system formulation may lead to a different mathematical appearance of the equations of motion while the physics behind is the same. The motion of the constrained bodies is described by means of equations that result basically from Newton’s second law. The equations are written for general motion of the single bodies with the addition of constraint conditions. Usually the equations of motions are derived from the Newton-Euler equationsNewton-Euler equations
The Newton–Euler equations describe the combined translational and rotational dynamics of a rigid body.With respect to a coordinate frame whose origin coincides with the body's center of mass, they can be expressed in matrix form as:...
or Lagrange’s equations
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
.
The motion of rigid bodies is described by means of
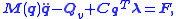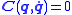(1) (2)This type of the equations of motion is based on so-called redundant coordinates, because the equations use more coordinates than degrees of freedom of the underlying system. The generalized coordinates are denoted by
, the mass matrixMass matrix
In computational mechanics, a mass matrix is a generalization of the concept of mass to generalized coordinates. For example, consider a two-body particle system in one dimension...
is represented by
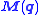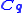which may depend on the generalized coordinates. represents the constraint conditions and the matrix (sometimes termed the Jacobian) is the derivation of the constraint conditions with respect to the coordinates. This matrix is used to apply constraint forces to the according equations of the bodies. The components of the vector are also denoted as Lagrange multipliers. In a rigid body, possible coordinates could be split into two parts,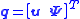where
represents translations and describes the rotations.Quadratic velocity vector
In the case of rigid bodies, the so-called quadratic velocity vector is used to describe Coriolis and centrifugal terms in the equations of motion. The name is because 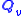includes quadratic terms of velocities and it results due to partial derivatives of the kinetic energy of the body.Lagrange multipliers
The Lagrange multiplier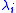 is related to a constraint condition 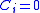and usually represents a force or a moment, which acts in “direction” of the constraint degree of freedom. The Lagrange multipliers do no "work" as compared to external forces that change the potential energy of a body.Minimal coordinates
The equations of motion (1,2) are represented by means of redundant coordinates, meaning that the coordinates are not independent. This can be exemplified by the slider-crank mechanism shown above, where each body has six degrees of freedom while most of the coordinates are dependent on the motion of the other bodies. For example, 18 coordinates and 17 constraints could be used to describe the motion of the slider-crank with rigid bodies. However, as there is only one degree of freedom, the equation of motion could be also represented by means of one equation and one degree of freedom, using e.g. the angle of the driving link as degree of freedom. The latter formulation has then the minimum number of coordinates in order to describe the motion of the system and can be thus called a minimal coordinates formulation. The transformation of redundant coordinates to minimal coordinates is sometimes cumbersome and only possible in the case of holonomic constraints and without kinematical loops. Several algorithms have been developed for the derivation of minimal coordinate equations of motion, to mention only the so-called recursive formulation. The resulting equations are easier to be solved because in the absence of constraint conditions, standard time integration methods can be used to integrate the equations of motion in time. While the reduced system might be solved more efficiently, the transformation of the coordinates might be computationally expensive. In very general multibody system formulations and computer codes, redundant coordinates are used in order to make the systems user-friendly and flexible.See also
- Flexible multibody systems (multibody systems where some bodies are flexible)
- Simulation of multibody systems (solution techniques)
- Dynamic simulationDynamic simulationDynamic simulation is the use of a computer program to model the time varying behavior of a system. The systems are typically described by ordinary differential equations or partial differential equations. As mathematical models incorporate real-world constraints, like gear backlash and rebound...
- Physics enginePhysics engineA physics engine is computer software that provides an approximate simulation of certain physical systems, such as rigid body dynamics , soft body dynamics, and fluid dynamics, of use in the domains of computer graphics, video games and film. Their main uses are in video games , in which case the...