Mutually unbiased bases
Encyclopedia
In quantum information
theory, mutually unbiased bases in Hilbert space
Cd are two orthonormal bases
and 
such that the square of the magnitude
of the inner product between any basis states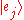
and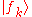 
equals the inverse
of the dimension
d:
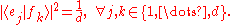
These bases are unbiased in the following sense: if a system is prepared in a state belonging to one of the bases, then all outcomes of the measurement
with respect to the other basis will occur with equal probabilities.
Another area where mutually unbiased bases can be applied is quantum key distribution, more specifically in secure quantum key exchange. Mutually unbiased bases are used in many protocols since the outcome is random when a measurement is made in a basis unbiased to that in which the state was prepared. When two remote parties share two non-orthogonal quantum states, attempts by an eavesdropper to distinguish between these by measurements will affect the system and this can be detected. While many quantum cryptography protocols have relied on 1-qubit
technologies, employing higher dimensional states, such as qutrits, allows for better security against eavesdropping. This motivates the study of mutually unbiased bases in higher-dimensional spaces.
Other uses of mutually unbiased bases include quantum state reconstruction
, quantum error correction codes
, and the so called "mean king's problem".
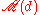denote the maximal number of mutually unbiased bases in the d-dimensional Hilbert space Cd. It is an open question how many mutually unbiased bases, 
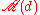, one can find in Cd, for arbitrary d.
In general, if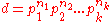
is the prime number decomposition
of d, where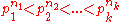
then the maximal number of mutually unbiased bases which can be constructed satisfies
It follows that if the dimension of a Hilbert space d is an integer power of a prime number, then it is possible to find d + 1 mutually unbiased bases. This can be seen in the previous equation, as the prime number decomposition of d simply is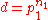
. Therefore,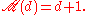
Though the maximal number of mutually unbiased bases is known when d is an integer power of a prime number, it is not known for arbitrary d.
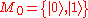
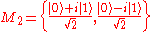
provides the simplest example of mutually unbiased bases in C2. The above bases are composed of the eigenvectors of the Pauli spin matrices
and their product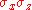 
.
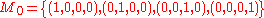
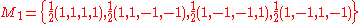
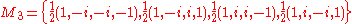
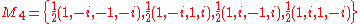
Weyl group
Let 
and 
be two unitary operators in the Hilbert space Cd such that
for some phase factor
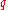. If 
is a primitive root of unity, for example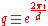 
then the eigenbases of 
and 
are mutually unbiased.
By choosing the eigenbasis of
to be the standard basis
, we can generate another basis unbiased to it using a Fourier matrix. The elements of the Fourier matrix are given by
Other bases which are unbiased to both the standard basis and the basis generated by the Fourier matrix can be generated using Weyl groups. The dimension of the Hilbert space is important when generating sets of mutually unbiased bases using Weyl groups. When d is a prime number, then the usual d + 1 mutually unbiased bases can be generated using Weyl groups. When d is not a prime number, then it is possible that the maximal number of mutually unbiased bases which can be generated using this method is 3.
, we define the unitary operators
and 
by
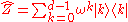
where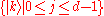
is the standard basis and 
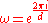is a root of unity
.
Then the eigenbases of the following d + 1 operators are mutually unbiased:
When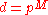
is a power of a prime, we make use of the Galois field 
to construct a maximal set of d + 1 mutually unbiased bases. We label the elements of the computational basis of Cd using the Galois field:
.
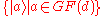We define the operators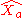
and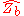 
in the following way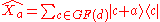
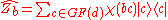
where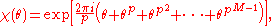
and the addition and multiplication in the kets and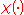
is that of 
.
Then we form d + 1 sets of commuting
unitary operators:
and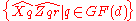 
for each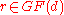 
The joint eigenbases of the operators in one set are mutually unbiased to that of any other set. We thus have d + 1 mutually unbiased bases.
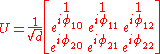
The problem of finding a set of k+1 mutually unbiased bases therefore corresponds to finding k mutually unbiased complex Hadamard matrices.
An example of a one parameter family of Hadamard matrices in a 4 dimensional Hilbert space is
.
.
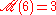Entropic uncertainty relations are analogous to the Heisenberg uncertainty principle
, and Maassen and Uffink found that for any two bases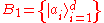
and 
:
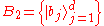where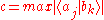
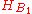and 
and 
is the respective entropy of the bases 
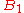and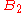 
, when measuring a given state.
Entropic uncertainty relations are often preferable to the Heisenberg uncertainty principle
, as they are not phrased in terms of the state to be measured, but in terms of c.
In scenarios such as quantum key distribution, we aim for measurement bases such that full knowledge of a state with respect to one basis implies minimal knowledge of the state with respect to the other bases. This implies a high entropy of measurement outcomes, and thus we call these strong entropic uncertainty relations.
For two bases, the lower bound of the uncertainty relation is maximized when the measurement bases are mutually unbiased, since mutually unbiased bases are maximally incompatible: the outcome of a measurement made in a basis unbiased to that in which the state is prepared in is completely random. In fact, for a d-dimensional space, we have: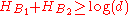
for any pair of mutually unbiased bases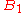
and 
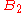. This bound is optimal: If we measure a state from one of the bases then the outcome has entropy 0 in that basis and an entropy of 
in the other.
If the dimension of the space is a prime power, we can construct d + 1 MUBs, and then it has been found that
which is stronger than the relation we would get from pairing up the sets and then using the Maassen and Uffink equation. Thus we have a characterization of d + 1 mutually unbiased bases as those for which the uncertainty relations are strongest.
Although the case for two bases, and for d + 1 bases is well studied, very little is known about uncertainty relations for mutually unbiased bases in other circumstances.
When considering more than two, and less than
bases it is known that large sets of mutually unbiased bases exist which exhibit very little uncertainty . This means merely being mutually unbiased does not lead to high uncertainty, except when considering measurements in only two bases. Yet there do exist other measurements that are very uncertain.
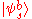and 
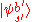are said to be mutually unbiased if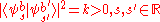
For the generalized position and momentum eigenstates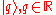
and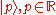 
, the value of k is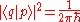
The existence of mutually unbiased bases in a continuous Hilbert space remains open for debate, as further research in their existence is required before any conclusions can be reached.
Position states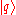
and momentum states 
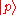are eigenvectors of Hermitian operators 
and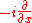 
, respectively. Weigert and Wilkinson were first to notice that also a linear combination of these operators have eigenbases, which have some features typical for the mutually unbiased bases. An operator 
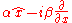has eigenfunctions proportional to 
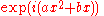with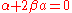 
and the corresponding eigenvalues 
. If we parametrize 
and 
as 
and 
, the overlap between any eigenstate of the linear combination and any eigenstate of the position operator (both states normalized to the Dirac delta) is constant, but dependent on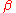 
:
where
and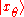 
stand for eigenfunctions of 
and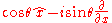 
.
Quantum information
In quantum mechanics, quantum information is physical information that is held in the "state" of a quantum system. The most popular unit of quantum information is the qubit, a two-level quantum system...
theory, mutually unbiased bases in Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
Cd are two orthonormal bases
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
and such that the square of the magnitudeMagnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
of the inner product between any basis states
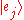and 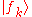equals the inverseMultiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of the dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
d:
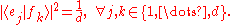
These bases are unbiased in the following sense: if a system is prepared in a state belonging to one of the bases, then all outcomes of the measurement
Measurement in quantum mechanics
The framework of quantum mechanics requires a careful definition of measurement. The issue of measurement lies at the heart of the problem of the interpretation of quantum mechanics, for which there is currently no consensus....
with respect to the other basis will occur with equal probabilities.
Overview
The notion of mutually unbiased bases was first introduced by Schwinger in 1960, and the first person to consider applications of mutually unbiased bases was Ivanovic in the problem of quantum state determination.Another area where mutually unbiased bases can be applied is quantum key distribution, more specifically in secure quantum key exchange. Mutually unbiased bases are used in many protocols since the outcome is random when a measurement is made in a basis unbiased to that in which the state was prepared. When two remote parties share two non-orthogonal quantum states, attempts by an eavesdropper to distinguish between these by measurements will affect the system and this can be detected. While many quantum cryptography protocols have relied on 1-qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
technologies, employing higher dimensional states, such as qutrits, allows for better security against eavesdropping. This motivates the study of mutually unbiased bases in higher-dimensional spaces.
Other uses of mutually unbiased bases include quantum state reconstruction
Quantum tomography
Quantum tomography or quantum state tomography is the process of reconstructing the quantum state for a source of quantum systems by measurements on the systems coming from the source. The source may be any device or system which prepares quantum states either consistently into quantum pure states...
, quantum error correction codes
Quantum error correction
Quantum error correction is used in quantum computing to protect quantum information from errors due to decoherence and other quantum noise. Quantum error correction is essential if one is to achieve fault-tolerant quantum computation that can deal not only with noise on stored quantum...
, and the so called "mean king's problem".
Existence problem
Let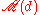 denote the maximal number of mutually unbiased bases in the d-dimensional Hilbert space Cd. It is an open question how many mutually unbiased bases, 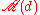, one can find in Cd, for arbitrary d.In general, if
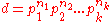
is the prime number decomposition
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
of d, where
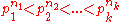
then the maximal number of mutually unbiased bases which can be constructed satisfies
It follows that if the dimension of a Hilbert space d is an integer power of a prime number, then it is possible to find d + 1 mutually unbiased bases. This can be seen in the previous equation, as the prime number decomposition of d simply is
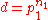. Therefore,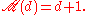Though the maximal number of mutually unbiased bases is known when d is an integer power of a prime number, it is not known for arbitrary d.
Example for d = 2
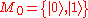
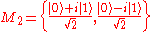
The three basesprovides the simplest example of mutually unbiased bases in C2. The above bases are composed of the eigenvectors of the Pauli spin matrices
and their product 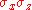.Example for d = 4
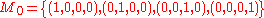
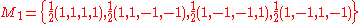
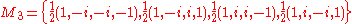
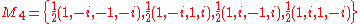
For d = 4, an example of d + 1 = 5 mutually unbiased bases where each basis is denoted as Mj, 0 ≤ j ≤ 4, is given as follows: Weyl groupWeyl groupIn mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
method
Let and be two unitary operators in the Hilbert space Cd such thatfor some phase factor
Phase factor
For any complex number written in polar form , the phase factor is the exponential part, i.e. eiθ. As such, the term "phase factor" is similar to the term phasor, although the former term is more common in quantum mechanics. This phase factor is itself a complex number of absolute value 1...
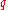. If is a primitive root of unity, for example 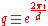then the eigenbases of and are mutually unbiased.By choosing the eigenbasis of
to be the standard basisStandard basis
In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
, we can generate another basis unbiased to it using a Fourier matrix. The elements of the Fourier matrix are given by
Other bases which are unbiased to both the standard basis and the basis generated by the Fourier matrix can be generated using Weyl groups. The dimension of the Hilbert space is important when generating sets of mutually unbiased bases using Weyl groups. When d is a prime number, then the usual d + 1 mutually unbiased bases can be generated using Weyl groups. When d is not a prime number, then it is possible that the maximal number of mutually unbiased bases which can be generated using this method is 3.
Unitary operators method using Galois fields
When d = p is primePrime
A prime is a natural number that has exactly two distinct natural number divisors: 1 and itself.Prime or PRIME may also refer to:In mathematics:*Prime , the ′ mark, typically used as a suffix...
, we define the unitary operators
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
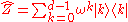
and bywhere
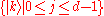is the standard basis and 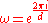is a root of unityRoot of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
.
Then the eigenbases of the following d + 1 operators are mutually unbiased:
When
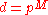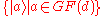is a power of a prime, we make use of the Galois field to construct a maximal set of d + 1 mutually unbiased bases. We label the elements of the computational basis of Cd using the Galois field:.We define the operators
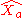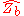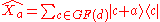
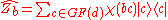
and in the following waywhere
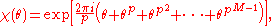
and the addition and multiplication in the kets and
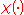is that of .Then we form d + 1 sets of commuting
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
unitary operators:
and 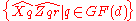for each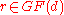 The joint eigenbases of the operators in one set are mutually unbiased to that of any other set. We thus have d + 1 mutually unbiased bases.
Hadamard matrix method
Given that one basis in a Hilbert space is the standard basis, then all bases which are unbiased with respect to this basis can be represented by the columns of a complex Hadamard matrix multiplied by a normalization factor. For d = 3 these matrices would have the form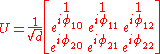The problem of finding a set of k+1 mutually unbiased bases therefore corresponds to finding k mutually unbiased complex Hadamard matrices.
An example of a one parameter family of Hadamard matrices in a 4 dimensional Hilbert space is
The problem of finding a maximal set of MUBs when d = 6
The smallest dimension that is not an integer power of a prime is d = 6. This is also the smallest dimension for which the number of mutually unbiased bases is not known. The methods used to determine the number of mutually unbiased bases when d is an integer power of a prime number cannot be used in this case. Searches for a set of four mutually unbiased bases when d = 6, both by using Hadamard matrices and numerical methods have been unsuccessful. The general belief is that the maximum number of mutually unbiased bases for d = 6 is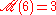.Entropic Uncertainty Relations and MUBs
There is an alternative characterization of mutually unbiased bases that considers them in terms of uncertainty relationsUncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
.
Entropic uncertainty relations are analogous to the Heisenberg uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
, and Maassen and Uffink found that for any two bases
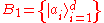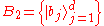and :where
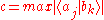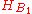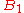and and is the respective entropy of the bases and 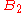, when measuring a given state.Entropic uncertainty relations are often preferable to the Heisenberg uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
, as they are not phrased in terms of the state to be measured, but in terms of c.
In scenarios such as quantum key distribution, we aim for measurement bases such that full knowledge of a state with respect to one basis implies minimal knowledge of the state with respect to the other bases. This implies a high entropy of measurement outcomes, and thus we call these strong entropic uncertainty relations.
For two bases, the lower bound of the uncertainty relation is maximized when the measurement bases are mutually unbiased, since mutually unbiased bases are maximally incompatible: the outcome of a measurement made in a basis unbiased to that in which the state is prepared in is completely random. In fact, for a d-dimensional space, we have:
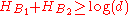
for any pair of mutually unbiased bases
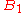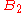and . This bound is optimal: If we measure a state from one of the bases then the outcome has entropy 0 in that basis and an entropy of in the other.If the dimension of the space is a prime power, we can construct d + 1 MUBs, and then it has been found that
which is stronger than the relation we would get from pairing up the sets and then using the Maassen and Uffink equation. Thus we have a characterization of d + 1 mutually unbiased bases as those for which the uncertainty relations are strongest.
Although the case for two bases, and for d + 1 bases is well studied, very little is known about uncertainty relations for mutually unbiased bases in other circumstances.
When considering more than two, and less than
bases it is known that large sets of mutually unbiased bases exist which exhibit very little uncertainty . This means merely being mutually unbiased does not lead to high uncertainty, except when considering measurements in only two bases. Yet there do exist other measurements that are very uncertain.Mutually unbiased bases in infinite dimension Hilbert spaces
While there has been investigation into mutually unbiased bases in infinite dimension Hilbert space, their existence remains an open question. It is conjectured that in a continuous Hilbert space, two orthonormal basesOrthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
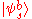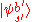and are said to be mutually unbiased if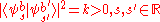For the generalized position and momentum eigenstates
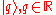and 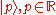, the value of k is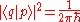The existence of mutually unbiased bases in a continuous Hilbert space remains open for debate, as further research in their existence is required before any conclusions can be reached.
Position states
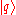and momentum states 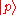are eigenvectors of Hermitian operators and 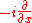, respectively. Weigert and Wilkinson were first to notice that also a linear combination of these operators have eigenbases, which have some features typical for the mutually unbiased bases. An operator 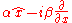has eigenfunctions proportional to 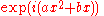with 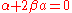and the corresponding eigenvalues . If we parametrize and as and , the overlap between any eigenstate of the linear combination and any eigenstate of the position operator (both states normalized to the Dirac delta) is constant, but dependent on 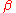:where
and 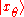stand for eigenfunctions of and 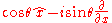.