
Nambu mechanics
Encyclopedia
In mathematics
, Nambu dynamics is a generalization of Hamiltonian mechanics
involving multiple Hamiltonians. Recall that Hamiltonian mechanics
is based upon the flows generated by a smooth
Hamiltonian over a symplectic manifold
. The flows are symplectomorphism
s and hence obey Liouville's theorem
. This was soon generalized to flows generated by a Hamiltonian over a Poisson manifold
. In 1973, Yoichiro Nambu
suggested a generalization involving Nambu-Poisson manifolds with more than one Hamiltonian.
Specifically, consider a differential manifold M, for some integer N ≥ 2; one has a smooth N-linear map from N copies of C ∞ (M) to itself, such that it is completely antisymmetric:
the Nambu bracket, {h1, ..., hN−1, .},
which acts as a derivation
{h1, ..., hN−1,fg} = {h1, ..., hN−1, f} g + f {h1, ..., hN−1, g}; whence the Filippov Identities (FI), (evocative of the Jacobi identities,
but unlike them, not antisymmetrized in all arguments, for N ≥ 2 ):
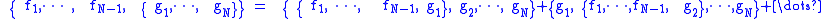
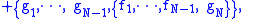
so that {f1, ..., fN−1, •} acts as a generalized derivation
over the N-fold product {. ,..., .}.
There are N − 1 Hamiltonians, H1, ..., HN−1, generating an incompressible flow
,
The generalized phase-space velocity is divergenceless, enabling Liouville's theorem
.
The case N = 2 reduces to a Poisson manifold
, and conventional Hamiltonian mechanics.
For larger even N, the N − 1 Hamiltonians identify with the maximal number of independent invariants of motion (cf. Conserved quantity
) characterizing a superintegrable system
which evolves in N-dimensional phase space. Such systems are also describable by conventional Hamiltonian dynamics; but their description in the framework of Nambu mechanics is substantially more elegant and intuitive, as all invariants enjoy the same geometrical status as the Hamiltonian: the trajectory in phase space is the intersection of the N − 1 hypersurfaces specified by these invariants. Thus, the flow is perpendicular to all N − 1 gradients of these Hamiltonians, whence parallel to the generalized cross product specified by the respective Nambu bracket.
Quantizing
Nambu dynamics leads to intriguing structures which coincide with conventional quantization ones when superintegrable systems are involved—as they must.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Nambu dynamics is a generalization of Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
involving multiple Hamiltonians. Recall that Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
is based upon the flows generated by a smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
Hamiltonian over a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
. The flows are symplectomorphism
Symplectomorphism
In mathematics, a symplectomorphism is an isomorphism in the category of symplectic manifolds.-Formal definition:A diffeomorphism between two symplectic manifolds f: \rightarrow is called symplectomorphism, iff^*\omega'=\omega,...
s and hence obey Liouville's theorem
Liouville's theorem
Liouville's theorem has various meanings, all mathematical results named after Joseph Liouville:*In complex analysis, see Liouville's theorem ; there is also a related theorem on harmonic functions....
. This was soon generalized to flows generated by a Hamiltonian over a Poisson manifold
Poisson manifold
In mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
. In 1973, Yoichiro Nambu
Yoichiro Nambu
is a Japanese-born American physicist, currently a professor at the University of Chicago. Known for his contributions to the field of theoretical physics, he was awarded a one-half share of the Nobel Prize in Physics in 2008 for the discovery of the mechanism of spontaneous broken symmetry in...
suggested a generalization involving Nambu-Poisson manifolds with more than one Hamiltonian.
Specifically, consider a differential manifold M, for some integer N ≥ 2; one has a smooth N-linear map from N copies of C ∞ (M) to itself, such that it is completely antisymmetric:
the Nambu bracket, {h1, ..., hN−1, .},
which acts as a derivation
Derivation
Derivation may refer to:* Derivation , a function on an algebra which generalizes certain features of the derivative operator* Derivation * Derivation in differential algebra, a unary function satisfying the Leibniz product law...
{h1, ..., hN−1,fg} = {h1, ..., hN−1, f} g + f {h1, ..., hN−1, g}; whence the Filippov Identities (FI), (evocative of the Jacobi identities,
but unlike them, not antisymmetrized in all arguments, for N ≥ 2 ):
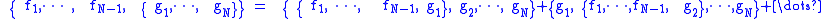
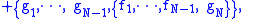
so that {f1, ..., fN−1, •} acts as a generalized derivation
Derivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
over the N-fold product {. ,..., .}.
There are N − 1 Hamiltonians, H1, ..., HN−1, generating an incompressible flow
Incompressible flow
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...
,
-
- d⁄dt f= {f, H1, ..., HN−1}.
The generalized phase-space velocity is divergenceless, enabling Liouville's theorem
Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
.
The case N = 2 reduces to a Poisson manifold
Poisson manifold
In mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
, and conventional Hamiltonian mechanics.
For larger even N, the N − 1 Hamiltonians identify with the maximal number of independent invariants of motion (cf. Conserved quantity
Conserved quantity
In mathematics, a conserved quantity of a dynamical system is a function H of the dependent variables that is a constant along each trajectory of the system. A conserved quantity can be a useful tool for qualitative analysis...
) characterizing a superintegrable system
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
which evolves in N-dimensional phase space. Such systems are also describable by conventional Hamiltonian dynamics; but their description in the framework of Nambu mechanics is substantially more elegant and intuitive, as all invariants enjoy the same geometrical status as the Hamiltonian: the trajectory in phase space is the intersection of the N − 1 hypersurfaces specified by these invariants. Thus, the flow is perpendicular to all N − 1 gradients of these Hamiltonians, whence parallel to the generalized cross product specified by the respective Nambu bracket.
Quantizing
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
Nambu dynamics leads to intriguing structures which coincide with conventional quantization ones when superintegrable systems are involved—as they must.
See also
- Hamiltonian mechanicsHamiltonian mechanicsHamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
- symplectic manifoldSymplectic manifoldIn mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
- Poisson manifoldPoisson manifoldIn mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
- Poisson algebraPoisson algebraIn mathematics, a Poisson algebra is an associative algebra together with a Lie bracket that also satisfies Leibniz' law; that is, the bracket is also a derivation. Poisson algebras appear naturally in Hamiltonian mechanics, and are also central in the study of quantum groups...
- Integrable systemIntegrable systemIn mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
- Conserved quantityConserved quantityIn mathematics, a conserved quantity of a dynamical system is a function H of the dependent variables that is a constant along each trajectory of the system. A conserved quantity can be a useful tool for qualitative analysis...

