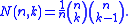Narayana number
Encyclopedia
In combinatorics
, the Narayana numbers N(n, k), n = 1, 2, 3 ..., 1 ≤ k ≤ n, form a triangular array
of natural number
s, called Narayana triangle, that occur in various counting problems. They are named for T.V. Narayana (1930–1987), a mathematician
from India
.
The Narayana numbers can be expressed in terms of binomial coefficient
s:
An example of a counting problem whose solution can be given in terms of the Narayana numbers N(n, k), is the number of expressions containing n pairs of parentheses which are correctly matched and which contain k distinct nestings. For instance, N(4, 2) = 6 as with four pairs of parentheses six sequences can be created which each contain two times the sub-pattern '':
(()) ()() (()) (()) (()) (())
From this example it should be obvious that N(n, 1) = 1, since the only way to get a single sub-pattern '' is to have all the opening parentheses in the first n positions, followed by all the closing parentheses. Also N(n, n) = 1, as distinct nestings can be achieved only by the repetitive pattern ... . More generally, it can be shown that the Narayana triangle is symmetric: N(n, k) = N(n, n − k + 1).
The first eight rows of the Narayana triangle read:
k = 1 2 3 4 5 6 7 8
n = 1 1
2 1 1
3 1 3 1
4 1 6 6 1
5 1 10 20 10 1
6 1 15 50 50 15 1
7 1 21 105 175 105 21 1
8 1 28 196 490 490 196 28 1
The sum of the rows in this triangle equal the Catalan numbers:
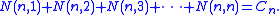
To illustrate this relationship, the Narayana numbers also count the number of paths from (0, 0) to (2n, 0), with steps only northeast and southeast, not straying below the x-axis, with k peaks.
The following figures represent the Narayana numbers N(4, k):
The sum of N(4, k) is 1 + 6 + 6 + 1, or 14, which is the same as Catalan number C4. This sum coincides with the interpretation of Catalan numbers as the number of monotonic paths along the edges of an n × n grid that do not pass above the diagonal.
different ways, where 
is the nth Bell number
. Furthermore, the number of ways to partition a set into exactly k partitions we use the Stirling numbers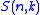
. Both of these concepts are a bit off-topic, but a necessary foundation for understanding the use of the Narayana numbers. In both of the above two notions crossing partitions are accounted for.
To reject the crossing partitions and count only the non-crossing partitions, we may use the Catalan number
s to count the non-crossing partitions of all n elements of the set,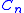
. To count the non-crossing partitions in which the set is partitioned in exactly k ways, we use the Narayana number 
.
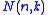Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, the Narayana numbers N(n, k), n = 1, 2, 3 ..., 1 ≤ k ≤ n, form a triangular array
Triangular array
In mathematics and computing, a triangular array of numbers, polynomials, or the like, is a doubly indexed sequence in which each row is only as long as the row's own index.Notable particular examples include these:...
of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, called Narayana triangle, that occur in various counting problems. They are named for T.V. Narayana (1930–1987), a mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
from India
India
India , officially the Republic of India , is a country in South Asia. It is the seventh-largest country by geographical area, the second-most populous country with over 1.2 billion people, and the most populous democracy in the world...
.
The Narayana numbers can be expressed in terms of binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s:
An example of a counting problem whose solution can be given in terms of the Narayana numbers N(n, k), is the number of expressions containing n pairs of parentheses which are correctly matched and which contain k distinct nestings. For instance, N(4, 2) = 6 as with four pairs of parentheses six sequences can be created which each contain two times the sub-pattern '':
(()) ()() (()) (()) (()) (())
From this example it should be obvious that N(n, 1) = 1, since the only way to get a single sub-pattern '' is to have all the opening parentheses in the first n positions, followed by all the closing parentheses. Also N(n, n) = 1, as distinct nestings can be achieved only by the repetitive pattern ... . More generally, it can be shown that the Narayana triangle is symmetric: N(n, k) = N(n, n − k + 1).
The first eight rows of the Narayana triangle read:
k = 1 2 3 4 5 6 7 8
n = 1 1
2 1 1
3 1 3 1
4 1 6 6 1
5 1 10 20 10 1
6 1 15 50 50 15 1
7 1 21 105 175 105 21 1
8 1 28 196 490 490 196 28 1
The sum of the rows in this triangle equal the Catalan numbers:
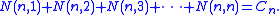
To illustrate this relationship, the Narayana numbers also count the number of paths from (0, 0) to (2n, 0), with steps only northeast and southeast, not straying below the x-axis, with k peaks.
The following figures represent the Narayana numbers N(4, k):
| N(4, k) | Paths |
|---|---|
| N(4, 1) = 1 path with 1 peak: |  |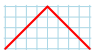
| N(4, 2) = 6 paths with 2 peaks: |  |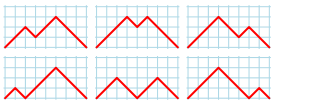
| N(4, 3) = 6 paths with 3 peaks: |  |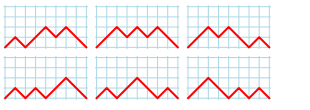
| N(4, 4) = 1 path with 4 peaks: |  |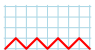
The sum of N(4, k) is 1 + 6 + 6 + 1, or 14, which is the same as Catalan number C4. This sum coincides with the interpretation of Catalan numbers as the number of monotonic paths along the edges of an n × n grid that do not pass above the diagonal.
Partitions
In the study of partitions, we see that in a set containing n elements, we may partition that set in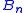 different ways, where 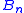is the nth Bell numberBell number
In combinatorics, the nth Bell number, named after Eric Temple Bell, is the number of partitions of a set with n members, or equivalently, the number of equivalence relations on it...
. Furthermore, the number of ways to partition a set into exactly k partitions we use the Stirling numbers
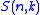. Both of these concepts are a bit off-topic, but a necessary foundation for understanding the use of the Narayana numbers. In both of the above two notions crossing partitions are accounted for.To reject the crossing partitions and count only the non-crossing partitions, we may use the Catalan number
Catalan number
In combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involvingrecursively defined objects...
s to count the non-crossing partitions of all n elements of the set,
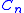. To count the non-crossing partitions in which the set is partitioned in exactly k ways, we use the Narayana number 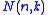.See also
- Catalan numberCatalan numberIn combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involvingrecursively defined objects...
- Delannoy numberDelannoy numberIn mathematics, a Delannoy number D describes the number of paths from the southwest corner of a rectangular grid to the northeast corner , using only single steps north, northeast, or east....
- Motzkin numberMotzkin numberIn mathematics, a Motzkin number for a given number n is the number of different ways of drawing non-intersecting chords on a circle between n points. The Motzkin numbers have very diverse applications in geometry, combinatorics and number theory...
- Schröder numberSchröder numberIn mathematics, a Schröder number describes the number of paths from the southwest corner of an n × n grid to the northeast corner , using only single steps north, northeast, or east, that do not rise above the SW–NE diagonal.The first few Schröder numbers are-Examples:The following...
- Pascal's trianglePascal's triangleIn mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...