Neo-Hookean solid
Encyclopedia
A Neo-Hookean solid is a hyperelastic material
model, similar to Hooke's law
, that can be used for predicting the nonlinear stress-strain behavior of materials undergoing large deformations. The model was proposed by Ronald Rivlin
in 1948. In contrast to linear elastic
materials, a the stress-strain curve
of a neo-Hookean material is not linear
. Instead, the relationship between applied stress and strain is initially linear, but at a certain point the stress-strain curve will plateau. The neo-Hookean model does not account for the dissipative
release of energy as heat while straining the material and perfect elasticity is assumed at all stages of deformation.
The neo-Hookean model is based on the statistical thermodynamics of cross-linked polymer chains and is usable for plastic
s and rubber
-like substances. Cross-linked polymers will act in a neo-Hookean manner because initially the polymer chains can move relative to each other when a stress is applied. However, at a certain point the polymer chains will be stretched to the maximum point that the covalent cross links will allow, and this will cause a dramatic increase in the elastic modulus of the material. The neo-Hookean material model does not predict that increase in modulus at large strains and is typically accurate only for strains less than 20%. The model is also inadequate for biaxial states of stress and has been superseded by the Mooney-Rivlin model.
The strain energy density function
for an incompressible neo-Hookean material is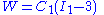
where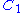
is a material constant, and 
is the first invariant
of the left Cauchy-Green deformation tensor, i.e.,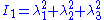
where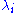
are the principal stretches.
For a compressible neo-Hookean material the strain energy density function is given by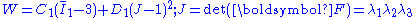
where
is a material constant,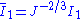 
is the first invariant of the deviatoric part of the left Cauchy-Green deformation tensor, and 
is the deformation gradient. Several alternative formulations exist for compressible neo-Hookean materials, for example 
For consistency with linear elasticity,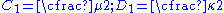
where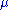
is the shear modulus and 
is the bulk modulus
.
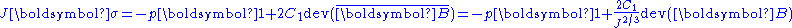
where
is the left Cauchy-Green deformation tensor, and
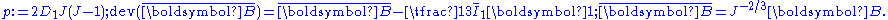
For infinitesimal strains (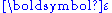
)
and the Cauchy stress can be expressed as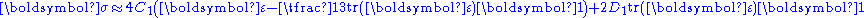
Comparison with Hooke's law
shows that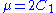
and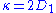 
.
where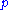
is an undetermined pressure.
, the principal components of the Cauchy stress are given by
Therefore, the differences between the principal stresses are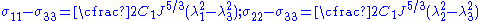
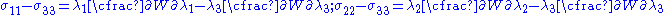
For an incompressible neo-Hookean material,
Therefore,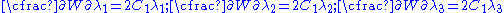
which gives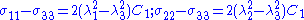
Hence, the true (Cauchy) stresses for a compressible neo-Hookean material are given by
The stress differences are given by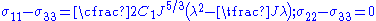
If the material is unconstrained we have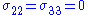
. Then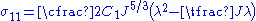
Equating the two expressions for
gives a relation for 
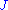as a function of 
, i.e.,
or
The above equation can be solved numerically using a Newton-Raphson iterative root finding procedure.
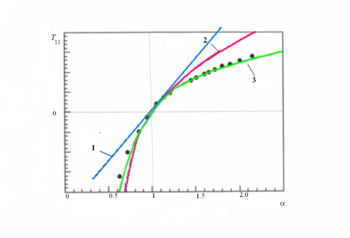Under uniaxial extension, 
and 
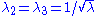. Therefore,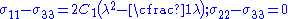
Assuming no traction on the sides,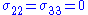
, so we can write
where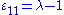
is the engineering strain. This equation is often written in alternative notation as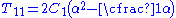
The equation above is for the true stress (ratio of the elongation force to deformed cross-section). For the engineering stress the equation is:
For small deformations
we will have:
Thus, the equivalent Young's modulus
of a neo-Hookean solid in uniaxial extension is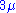
.
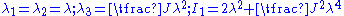
Therefore,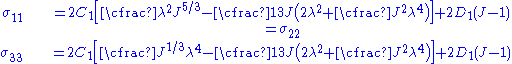
The stress differences are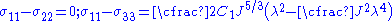
If the material is in a state of plane stress then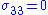
and we have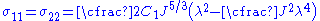
We also have a relation between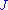
and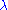 
:
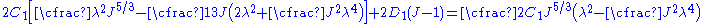
or,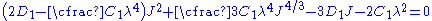
This equation can be solved for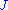
using Newton's method.
and the differences between the principal Cauchy stresses take the form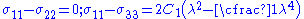
Under plane stress conditions we have
Therefore, the principal Cauchy stresses for a compressible neo-Hookean material are given by
If the material is incompressible then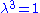
and the principal stresses can be arbitrary.
The figures below show that extremely high stresses are needed to achieve large triaxial extensions or compressions. Equivalently, relatively small triaxial stretch states can cause very high stresses to develop in a rubber-like material. Note also that the magnitude of the stress is quite sensitive to the bulk modulus but not to the shear modulus.
the deformation gradient in terms of components with respect to a reference basis is of the form
where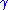
is the shear deformation. Therefore the left Cauchy-Green deformation tensor is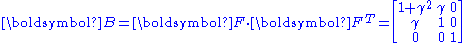
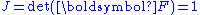. Hence, 
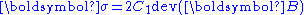. Now,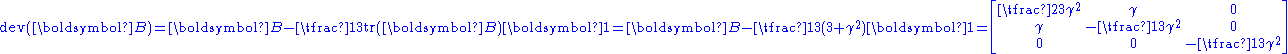
Hence the Cauchy stress is given by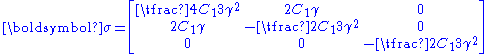
Thus neo-Hookean solid shows linear dependence of shear stresses upon shear deformation and quadratic dependence of the normal stress difference on the shear deformation. Note that the expressions for the Cauchy stress for a compressible and an incompressible neo-Hookean material in simple shear represent the same quantity and provide a means of determining the unknown pressure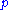
.
Hyperelastic material
A hyperelastic or Green elastic material is a type of constitutive model for ideally elastic material for which the stress-strain relationship derives from a strain energy density function. The hyperelastic material is a special case of a Cauchy elastic material.For many materials, linear elastic...
model, similar to Hooke's law
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
, that can be used for predicting the nonlinear stress-strain behavior of materials undergoing large deformations. The model was proposed by Ronald Rivlin
Ronald Rivlin
Ronald Samuel Rivlin was a British-American physicist, mathematician, rheologist and a noted expert on rubber.-Life:Rivlin was born in London in 1915. He studied physics and mathematics at St John's College, Cambridge, being awarded a BA in 1937 and a ScD in 1952...
in 1948. In contrast to linear elastic
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
materials, a the stress-strain curve
Stress-strain curve
During tensile testing of a material sample, the stress–strain curve is a graphical representation of the relationship between stress, derived from measuring the load applied on the sample, and strain, derived from measuring the deformation of the sample, i.e. elongation, compression, or distortion...
of a neo-Hookean material is not linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
. Instead, the relationship between applied stress and strain is initially linear, but at a certain point the stress-strain curve will plateau. The neo-Hookean model does not account for the dissipative
Dissipation
In physics, dissipation embodies the concept of a dynamical system where important mechanical models, such as waves or oscillations, lose energy over time, typically from friction or turbulence. The lost energy converts into heat, which raises the temperature of the system. Such systems are called...
release of energy as heat while straining the material and perfect elasticity is assumed at all stages of deformation.
The neo-Hookean model is based on the statistical thermodynamics of cross-linked polymer chains and is usable for plastic
Plastic
A plastic material is any of a wide range of synthetic or semi-synthetic organic solids used in the manufacture of industrial products. Plastics are typically polymers of high molecular mass, and may contain other substances to improve performance and/or reduce production costs...
s and rubber
Rubber
Natural rubber, also called India rubber or caoutchouc, is an elastomer that was originally derived from latex, a milky colloid produced by some plants. The plants would be ‘tapped’, that is, an incision made into the bark of the tree and the sticky, milk colored latex sap collected and refined...
-like substances. Cross-linked polymers will act in a neo-Hookean manner because initially the polymer chains can move relative to each other when a stress is applied. However, at a certain point the polymer chains will be stretched to the maximum point that the covalent cross links will allow, and this will cause a dramatic increase in the elastic modulus of the material. The neo-Hookean material model does not predict that increase in modulus at large strains and is typically accurate only for strains less than 20%. The model is also inadequate for biaxial states of stress and has been superseded by the Mooney-Rivlin model.
The strain energy density function
Strain energy density function
A strain energy density function or stored energy density function is a scalar valued function that relates the strain energy density of a material to the deformation gradient....
for an incompressible neo-Hookean material is
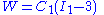
where
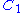is a material constant, and is the first invariantInvariants of tensors
In mathematics, in the fields of multilinear algebra and representation theory, invariants of tensors are coefficients of the characteristic polynomial of the tensor A:\ p:=\det ,...
of the left Cauchy-Green deformation tensor, i.e.,
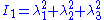
where
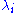are the principal stretches.For a compressible neo-Hookean material the strain energy density function is given by
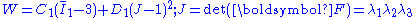
where
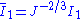is a material constant, is the first invariant of the deviatoric part of the left Cauchy-Green deformation tensor, and is the deformation gradient. Several alternative formulations exist for compressible neo-Hookean materials, for example For consistency with linear elasticity,
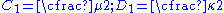
where
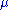is the shear modulus and is the bulk modulusBulk modulus
The bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
.
Compressible neo-Hookean material
For a compressible Rivlin neo-Hookean material the Cauchy stress is given by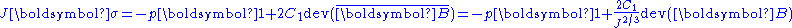where
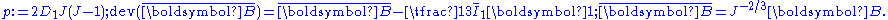
is the left Cauchy-Green deformation tensor, andFor infinitesimal strains (
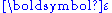)and the Cauchy stress can be expressed as
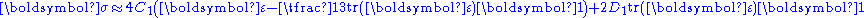
Comparison with Hooke's law
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
shows that
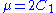and 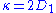.| Proof: |
|---|
The Cauchy stress Stress (physics) In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body... in a compressible hyperelastic material is given by  For a compressible Rivlin neo-Hookean material, 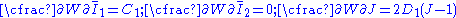 while, for a compressible Ogden neo-Hookean material, 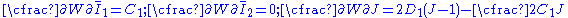 Therefore, the Cauchy stress in a compressible Rivlin neo-Hookean material is given by 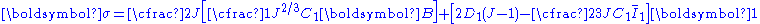 while that for the corresponding Ogden material is 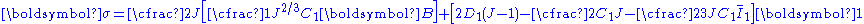 If the isochoric Isochoric Isochoric may refer to:*cell-transitive, in geometry*isochoric process, in chemistry or thermodynamics... part of the left Cauchy-Green deformation tensor is defined as 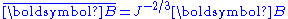 , then we can write the Rivlin neo-Heooken stress as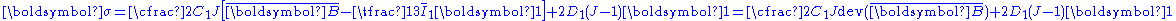 and the Ogden neo-Hookean stress as 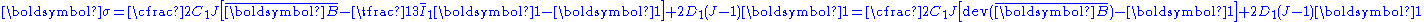 The quantities 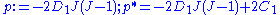 have the form of pressure Pressure Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :... s and are usually treated as such. The Rivlin neo-Hookean stress can then be expressed in the form  while the Ogden neo-Hookean stress has the form  |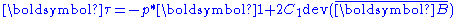
Incompressible neo-Hookean material
For an incompressible neo-Hookean material withwhere
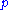is an undetermined pressure.Compressible Neo-Hookean material
For a compressible neo-Hookean hyperelastic materialHyperelastic material
A hyperelastic or Green elastic material is a type of constitutive model for ideally elastic material for which the stress-strain relationship derives from a strain energy density function. The hyperelastic material is a special case of a Cauchy elastic material.For many materials, linear elastic...
, the principal components of the Cauchy stress are given by
Therefore, the differences between the principal stresses are
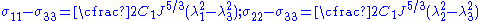
| Proof: |
|---|
For a compressible hyperelastic material Hyperelastic material A hyperelastic or Green elastic material is a type of constitutive model for ideally elastic material for which the stress-strain relationship derives from a strain energy density function. The hyperelastic material is a special case of a Cauchy elastic material.For many materials, linear elastic... , the principal components of the Cauchy stress are given by  The strain energy density function for a compressible neo Hookean material is  Therefore,  Since  we have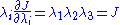 Hence, 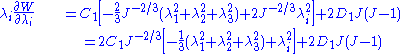 The principal Cauchy stresses are therefore given by  |
Incompressible Neo-Hookean material
In terms of the principal stretches, the Cauchy stress differences for an incompressible hyperelastic material are given by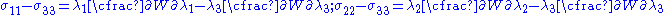For an incompressible neo-Hookean material,
Therefore,
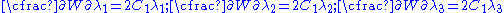
which gives
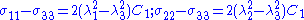
Compressible neo-Hookean material
For a compressible material undergoing uniaxial extension, the principal stretches areHence, the true (Cauchy) stresses for a compressible neo-Hookean material are given by
The stress differences are given by
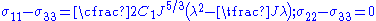
If the material is unconstrained we have
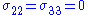. Then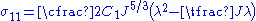Equating the two expressions for
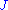gives a relation for as a function of , i.e.,or
The above equation can be solved numerically using a Newton-Raphson iterative root finding procedure.
Incompressible neo-Hookean material
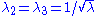and . Therefore,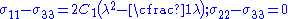Assuming no traction on the sides,
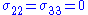, so we can writewhere
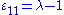is the engineering strain. This equation is often written in alternative notation as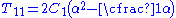The equation above is for the true stress (ratio of the elongation force to deformed cross-section). For the engineering stress the equation is:
For small deformations
we will have:Thus, the equivalent Young's modulus
Young's modulus
Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
of a neo-Hookean solid in uniaxial extension is
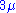.Compressible Neo-Hookean material
In the case of equibiaxial extension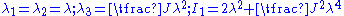Therefore,
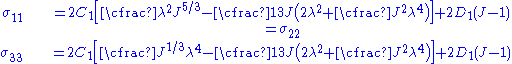
The stress differences are
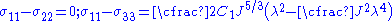
If the material is in a state of plane stress then
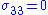and we have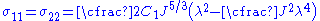We also have a relation between
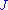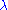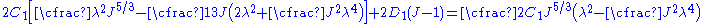
and :or,
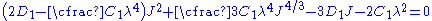
This equation can be solved for
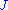using Newton's method.Incompressible Neo-Hookean material
For an incompressible material and the differences between the principal Cauchy stresses take the form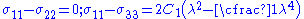Under plane stress conditions we have
Pure dilation
For the case of pure dilationTherefore, the principal Cauchy stresses for a compressible neo-Hookean material are given by
If the material is incompressible then
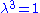and the principal stresses can be arbitrary.The figures below show that extremely high stresses are needed to achieve large triaxial extensions or compressions. Equivalently, relatively small triaxial stretch states can cause very high stresses to develop in a rubber-like material. Note also that the magnitude of the stress is quite sensitive to the bulk modulus but not to the shear modulus.
Simple shear
For the case of simple shearSimple shear
In fluid mechanics, simple shear is a special case of deformation where only one component of velocity vectors has a non-zero value:\ V_x=f\ V_y=V_z=0And the gradient of velocity is constant and perpendicular to the velocity itself:...
the deformation gradient in terms of components with respect to a reference basis is of the form
where
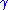is the shear deformation. Therefore the left Cauchy-Green deformation tensor is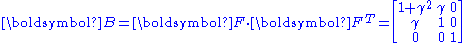Compressible Neo-Hookean material
In this case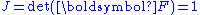. Hence, 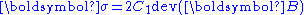. Now,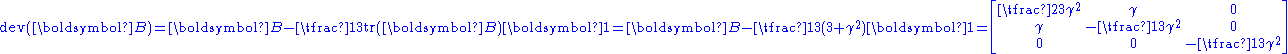Hence the Cauchy stress is given by
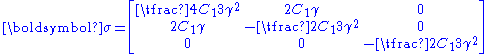
Incompressible Neo-Hookean material
Using the relation for the Cauchy stress for an incompressible neo-Hookean material we getThus neo-Hookean solid shows linear dependence of shear stresses upon shear deformation and quadratic dependence of the normal stress difference on the shear deformation. Note that the expressions for the Cauchy stress for a compressible and an incompressible neo-Hookean material in simple shear represent the same quantity and provide a means of determining the unknown pressure
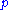.See also
- Hyperelastic materialHyperelastic materialA hyperelastic or Green elastic material is a type of constitutive model for ideally elastic material for which the stress-strain relationship derives from a strain energy density function. The hyperelastic material is a special case of a Cauchy elastic material.For many materials, linear elastic...
- Strain energy density functionStrain energy density functionA strain energy density function or stored energy density function is a scalar valued function that relates the strain energy density of a material to the deformation gradient....
- Mooney-Rivlin solid
- Finite strain theory
- Stress measuresStress measuresThe most commonly used measure of stress is the Cauchy stress. However, several other measures of stress can be defined. Some such stress measures that are widely used in continuum mechanics, particularly in the computational context, are:...