
Neutron transport
Encyclopedia
Neutron transport is the study of the motions and interactions of neutron
s with materials. Nuclear scientists and engineers often need to know where neutrons are in an apparatus, what direction they are going, and how quickly they are moving. It is commonly used to determine the behavior of nuclear reactor
cores and experimental or industrial neutron beam
s. Neutron transport is a type of radiative transport.
, which was used in the 1800s to study the kinetic theory of gases. It did not receive large-scale development until the invention of chain-reacting nuclear reactors in the 1940s. As neutron distributions came under detailed scrutiny, elegant approximations and analytic solutions were found in simple geometries. However, as computational power has increased, numerical approaches to neutron transport have become prevalent. Today, with massively parallel computers, neutron transport is still under very active development in academia and research institutions throughout the world.
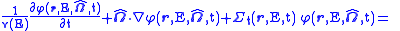
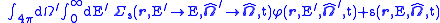
Where:
The transport equation can be applied to a given part of phase space (time t, energy E, location , and direction of travel
, and direction of travel  ). The first term represents the time rate of change of neutrons in the system. The second terms describes the movement of neutrons into or out of the volume of space of interest. The third term accounts for all neutrons that have a collision in that phase space. The first term on the right hand side is in-scattering, these are neutrons that enter this area of phase space as a result of scattering interactions in another. The second term on the right is a generic source. The equation is usually solved to find
). The first term represents the time rate of change of neutrons in the system. The second terms describes the movement of neutrons into or out of the volume of space of interest. The third term accounts for all neutrons that have a collision in that phase space. The first term on the right hand side is in-scattering, these are neutrons that enter this area of phase space as a result of scattering interactions in another. The second term on the right is a generic source. The equation is usually solved to find 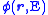 , since that will allow for the calculation of reaction rates, which are of primary interest in shielding and dosimetry studies.
, since that will allow for the calculation of reaction rates, which are of primary interest in shielding and dosimetry studies.
is the process through which a nucleus splits into (typically two) smaller atoms. If fission is occurring, it is often of interest to know the asymptotic behavior of the system. A reactor is called “critical” if the chain reaction is self-sustaining and time-independent. If the system is not in equilibrium the asymptotic neutron distribution, or the fundamental mode, will grow or decay exponentially over time.
Criticality calculations are used to analyze steady-state multiplying media (multiplying media can undergo fission), such as a critical nuclear reactor. The loss terms (absorption, out-scattering, and leakage) and the source terms (in-scatter and fission) are proportional to the neutron flux, contrasting with fixed-source problems where the source is independent of the flux. In these calculations, the presumption of time invariance requires that neutron production exactly equals neutron loss.
Since this criticality can only be achieved by very fine manipulations of the geometry (typically via control rods in a reactor), it is unlikely that the modeled geometry will be truly critical. To allow some flexibility in the way models are set up, these problems are formulated as eigenvalue problems, where one parameter is artificially modified until criticality is reached. The most common formulations are the time-absorption and the multiplication eigenvalues, also known as the alpha and k eigenvalues. The alpha and k are the tunable quanitites.
K-eigenvalue problems are the most common in nuclear reactor analysis. The number of neutrons produced per fission is multiplicatively modified by the dominant eigenvalue. The resulting value of this eigenvalue reflects the time dependence of the neutron density in a multiplying medium.
In the case of a nuclear reactor
, neutron flux and power density are proportional, hence during reactor start-up keff > 1, during reactor operation keff = 1 and keff < 1 at reactor shutdown.
or stochastic methods
. In deterministic methods the transport equation (or an approximation of it, such as diffusion theory
) is solved as a differential equation. In stochastic methods such as Monte Carlo
discrete particle histories are tracked and averaged in a random walk directed by measured interaction probabilities. Deterministic methods usually involve multi-group approaches while Monte Carlo can work with multi-group and continuous energy cross-section libraries. Multi-group calculations are usually iterative, because the group constants are calculated using flux-energy profiles, which are determined as the result of the neutron transport calculation.
.
Neutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
s with materials. Nuclear scientists and engineers often need to know where neutrons are in an apparatus, what direction they are going, and how quickly they are moving. It is commonly used to determine the behavior of nuclear reactor
Nuclear reactor
A nuclear reactor is a device to initiate and control a sustained nuclear chain reaction. Most commonly they are used for generating electricity and for the propulsion of ships. Usually heat from nuclear fission is passed to a working fluid , which runs through turbines that power either ship's...
cores and experimental or industrial neutron beam
Beam
Beam may refer to:*Beam , a construction element*Beam , the most extreme width of a nautical vessel, or a point alongside the ship at the mid-point of its length*A narrow, propagating stream of particles or energy:...
s. Neutron transport is a type of radiative transport.
Background
Neutron transport has roots in the Boltzmann equationBoltzmann equation
The Boltzmann equation, also often known as the Boltzmann transport equation, devised by Ludwig Boltzmann, describes the statistical distribution of one particle in rarefied gas...
, which was used in the 1800s to study the kinetic theory of gases. It did not receive large-scale development until the invention of chain-reacting nuclear reactors in the 1940s. As neutron distributions came under detailed scrutiny, elegant approximations and analytic solutions were found in simple geometries. However, as computational power has increased, numerical approaches to neutron transport have become prevalent. Today, with massively parallel computers, neutron transport is still under very active development in academia and research institutions throughout the world.
Neutron Transport Equation
The neutron transport equation is a balance statement that conserves neutrons. Each term represents a gain or a loss of a neutron, and the balance, in essence, claims that neutrons gained equals neutrons lost. It is formulated as follows: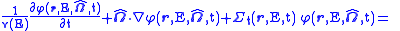
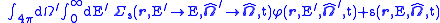
Where:
| Symbol | Meaning | Comments |
|---|---|---|
 |
Position vector (i.e. x,y,z) | |
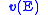 |
Neutron velocity vector | |
| Unit vector in direction of motion | ||
 |
Time | |
 |
Energy | |
 |
Angular neutron flux Number of neutrons in a differential volume 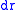 about about  , with a differential energy in , with a differential energy in  about about  , moving in a differential solid angle in , moving in a differential solid angle in  about about  , at time , at time  . . |
Note integrating over all angles yields Neutron Scalar Flux Neutron flux The neutron flux is a quantity used in reactor physics corresponding to the total length travelled by all neutrons per unit time and volume . The neutron fluence is defined as the neutron flux integrated over a certain time period.... 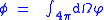 |
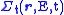 |
Macroscopic total cross section Nuclear cross section The nuclear cross section of a nucleus is used to characterize the probability that a nuclear reaction will occur. The concept of a nuclear cross section can be quantified physically in terms of "characteristic area" where a larger area means a larger probability of interaction... , which includes all possible interactions |
|
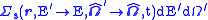 |
Double differential scattering cross section Characterizes scattering of a neutron from an incident energy  and direction and direction  to a final energy to a final energy 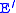 in in 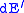 and direction and direction 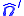 in in 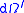 . . |
|
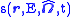 |
Source term | |
The transport equation can be applied to a given part of phase space (time t, energy E, location
 , and direction of travel
, and direction of travel  ). The first term represents the time rate of change of neutrons in the system. The second terms describes the movement of neutrons into or out of the volume of space of interest. The third term accounts for all neutrons that have a collision in that phase space. The first term on the right hand side is in-scattering, these are neutrons that enter this area of phase space as a result of scattering interactions in another. The second term on the right is a generic source. The equation is usually solved to find
). The first term represents the time rate of change of neutrons in the system. The second terms describes the movement of neutrons into or out of the volume of space of interest. The third term accounts for all neutrons that have a collision in that phase space. The first term on the right hand side is in-scattering, these are neutrons that enter this area of phase space as a result of scattering interactions in another. The second term on the right is a generic source. The equation is usually solved to find 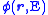 , since that will allow for the calculation of reaction rates, which are of primary interest in shielding and dosimetry studies.
, since that will allow for the calculation of reaction rates, which are of primary interest in shielding and dosimetry studies.Types of neutron transport calculations
Several basic types of neutron transport problems exist, depending on the type of problem being solved.Fixed Source
A fixed source calculation involves imposing a known neutron source on a medium and determining the resulting neutron distribution throughout the problem. This type of problem is particularly useful for shielding calculations, where a designer would like to minimize the neutron dose outside of a shield while using the least amount of shielding material. For instance, a spent nuclear fuel cask requires shielding calculations to determine how much concrete and steel is needed to safely protect the truck driver who is shipping it.Criticality
FissionNuclear fission
In nuclear physics and nuclear chemistry, nuclear fission is a nuclear reaction in which the nucleus of an atom splits into smaller parts , often producing free neutrons and photons , and releasing a tremendous amount of energy...
is the process through which a nucleus splits into (typically two) smaller atoms. If fission is occurring, it is often of interest to know the asymptotic behavior of the system. A reactor is called “critical” if the chain reaction is self-sustaining and time-independent. If the system is not in equilibrium the asymptotic neutron distribution, or the fundamental mode, will grow or decay exponentially over time.
Criticality calculations are used to analyze steady-state multiplying media (multiplying media can undergo fission), such as a critical nuclear reactor. The loss terms (absorption, out-scattering, and leakage) and the source terms (in-scatter and fission) are proportional to the neutron flux, contrasting with fixed-source problems where the source is independent of the flux. In these calculations, the presumption of time invariance requires that neutron production exactly equals neutron loss.
Since this criticality can only be achieved by very fine manipulations of the geometry (typically via control rods in a reactor), it is unlikely that the modeled geometry will be truly critical. To allow some flexibility in the way models are set up, these problems are formulated as eigenvalue problems, where one parameter is artificially modified until criticality is reached. The most common formulations are the time-absorption and the multiplication eigenvalues, also known as the alpha and k eigenvalues. The alpha and k are the tunable quanitites.
K-eigenvalue problems are the most common in nuclear reactor analysis. The number of neutrons produced per fission is multiplicatively modified by the dominant eigenvalue. The resulting value of this eigenvalue reflects the time dependence of the neutron density in a multiplying medium.
- keff < 1, subcritical: the neutron density is decreasing as time passes;
- keff = 1, critical: the neutron density remains unchanged; and
- keff > 1, supercritical: the neutron density is increasing with time.
In the case of a nuclear reactor
Nuclear reactor
A nuclear reactor is a device to initiate and control a sustained nuclear chain reaction. Most commonly they are used for generating electricity and for the propulsion of ships. Usually heat from nuclear fission is passed to a working fluid , which runs through turbines that power either ship's...
, neutron flux and power density are proportional, hence during reactor start-up keff > 1, during reactor operation keff = 1 and keff < 1 at reactor shutdown.
Computational Methods
Both fixed-source and criticality calculations can be solved using deterministic methodsDeterministic system (mathematics)
In mathematics, a deterministic system is a system in which no randomness is involved in the development of future states of the system. A deterministic model will thus always produce the same output from a given starting condition or initial state.-Examples:...
or stochastic methods
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
. In deterministic methods the transport equation (or an approximation of it, such as diffusion theory
Diffusion process
In probability theory, a branch of mathematics, a diffusion process is a solution to a stochastic differential equation. It is a continuous-time Markov process with continuous sample paths....
) is solved as a differential equation. In stochastic methods such as Monte Carlo
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
discrete particle histories are tracked and averaged in a random walk directed by measured interaction probabilities. Deterministic methods usually involve multi-group approaches while Monte Carlo can work with multi-group and continuous energy cross-section libraries. Multi-group calculations are usually iterative, because the group constants are calculated using flux-energy profiles, which are determined as the result of the neutron transport calculation.
Discretization in Deterministic Methods
To numerically solve the transport equation using algebraic equations on a computer, the spatial, angular, energy, and time variables must be discretizedDiscretization
In mathematics, discretization concerns the process of transferring continuous models and equations into discrete counterparts. This process is usually carried out as a first step toward making them suitable for numerical evaluation and implementation on digital computers...
.
- Spatial variables are typically discretized by simply breaking the geometry into many small regions on a mesh. The balance can then be solved at each mesh point using finite differenceFinite differenceA finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
or by nodal methods. - Angular variables can be discretized by discrete ordinates and weighting quadrature setsNumerical integrationIn numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
(giving rise to the SN methods), or by functional expansion methods with the spherical harmonicsSpherical harmonicsIn mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
(leading to the PN methods). - Energy variables are typically discretized by the multi-group method, where each energy group represents one constant energy. As few as 2 groups can be sufficient for some thermal reactor problems, but fast reactor calculations may require many more.
- The time variable is broken into discrete time steps, with time derivatives replaced with difference formulas.
Computer Codes Used In Neutron Transport
- MCNP - A LANLLos Alamos National LaboratoryLos Alamos National Laboratory is a United States Department of Energy national laboratory, managed and operated by Los Alamos National Security , located in Los Alamos, New Mexico...
developed Monte Carlo code for general radiation transport - NEWT - An ORNLOak Ridge National LaboratoryOak Ridge National Laboratory is a multiprogram science and technology national laboratory managed for the United States Department of Energy by UT-Battelle. ORNL is the DOE's largest science and energy laboratory. ORNL is located in Oak Ridge, Tennessee, near Knoxville...
developed 2-D SN code - DIF3D/VARIANT - An Argonne National Laboratory developed 3-D code originally developed for fast reactors
- DRAGON - An open-source lattice physics code
- Attila - A commercial transport code
- PARTISN
- KENO
- DANTSYS
- PHOENIX/ANC - A proprietary lattice-physics and global diffusion code suite from Westinghouse Electric
- DENOVO - A massively parallel transport code under development by ORNLOak Ridge National LaboratoryOak Ridge National Laboratory is a multiprogram science and technology national laboratory managed for the United States Department of Energy by UT-Battelle. ORNL is the DOE's largest science and energy laboratory. ORNL is located in Oak Ridge, Tennessee, near Knoxville...
- RAPTOR-M3G - A proprietary parallel radiation transport code developed by Westinghouse Electric
See also
- Nuclear ReactorNuclear reactorA nuclear reactor is a device to initiate and control a sustained nuclear chain reaction. Most commonly they are used for generating electricity and for the propulsion of ships. Usually heat from nuclear fission is passed to a working fluid , which runs through turbines that power either ship's...
- Boltzmann equationBoltzmann equationThe Boltzmann equation, also often known as the Boltzmann transport equation, devised by Ludwig Boltzmann, describes the statistical distribution of one particle in rarefied gas...
- TINTETime-dependent Neutronics and TemperaturesTIme-dependent Neutronics and TEmperatures is a two-group diffusion code for the study of nuclear and thermal behavior of high temperature reactors. It was developed by Forschungszentrum Jülich in Germany, formally known as KFA , to investigate HTGRs in 2D geometry....

