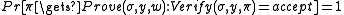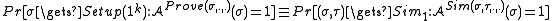Non-interactive zero-knowledge proof
Encyclopedia
Non-interactive zero-knowledge proofs are a variant of zero-knowledge proof
s. Blum
, Feldman, and Micali
showed that a common reference string shared between the prover and the verifier is enough to achieve computational zero-knowledge without requiring interaction. Goldreich
and Oren gave impossibility results for one shot zero-knowledge protocols in the standard model
. These two results are not contradictory, as the impossibility result of Goldreich and Oren does not hold in the common reference string model
or the random oracle model. Non-interactive zero-knowledge proofs however show a separation between the cryptographic tasks that can be achieved in the standard model and those that can be achieved in 'more powerful' extended models.
The model influences the properties that can be obtained from a zero-knowledge protocol. Pass showed that in the common reference string model non-interactive zero-knowledge protocols do not preserve all of the properties of interactive zero-knowledge protocols, e.g. they do not preserve deniability.
Non-interactive zero-knowledge proofs can also be obtained in the random oracle model using the Fiat-Shamir heuristic
.
A common reference string in general is not a random string. It may, for instance, consist of randomly chosen group elements that all protocol parties use. Although the group elements are random, the reference string is not as it contains a certain structure (e.g., group elements) that is distinguishable from randomness.
Subsequently, Feige, Lapidot, and Shamir
introduced multi-theorem zero-knowledge proofs as a more versatile notion for non-interactive zero knowledge proofs.
In this model the prover and the verifier are in possession of a reference string sampled from a distribution D by a trusted setup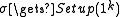
. To prove statement 
with witness w, the prover runs 
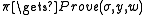and sends the proof 
to the verifier. The verifier accepts if 
, and rejects otherwise.
To account for the fact that
may influence the statements that are being proven, the witness relation can be
generalized to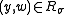
parameterized by
.
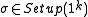and every 
.
More formally, for all k, all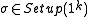
, and all 
:
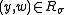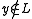except with some small probability. The upper bound of this probability is referred to as the soundness error of a proof system.
More formally, for every malicious prover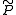
, there exists a negligible function 
such that
Zero-knowledge proof
In cryptography, a zero-knowledge proof or zero-knowledge protocol is an interactive method for one party to prove to another that a statement is true, without revealing anything other than the veracity of the statement....
s. Blum
Manuel Blum
Manuel Blum is a computer scientist who received the Turing Award in 1995 "In recognition of his contributions to the foundations of computational complexity theory and its application to cryptography and program checking".-Biography:Blum attended MIT, where he received his bachelor's degree and...
, Feldman, and Micali
Silvio Micali
Silvio Micali is an Italian-born computer scientist at MIT Computer Science and Artificial Intelligence Laboratory and a professor of computer science in MIT's Department of Electrical Engineering and Computer Science since 1983. His research centers on the theory of cryptography and information...
showed that a common reference string shared between the prover and the verifier is enough to achieve computational zero-knowledge without requiring interaction. Goldreich
Oded Goldreich
Oded Goldreich is a professor of Computer Science at the Faculty of Mathematics and Computer Science of Weizmann Institute of Science, Israel. His research interests lie within the theory of computation...
and Oren gave impossibility results for one shot zero-knowledge protocols in the standard model
Standard Model (cryptography)
In cryptography the standard model is the model of computation in which the adversary is only limited by the amount of time and computational power available. Other names used are bare model and plain model....
. These two results are not contradictory, as the impossibility result of Goldreich and Oren does not hold in the common reference string model
Common reference string model
In cryptography, the common reference string model captures the assumption that a trusted setup in which all involved parties get access to the same string crs taken from some distribution D exists. Schemes proven secure in the CRS model are secure given that the setup was performed correctly...
or the random oracle model. Non-interactive zero-knowledge proofs however show a separation between the cryptographic tasks that can be achieved in the standard model and those that can be achieved in 'more powerful' extended models.
The model influences the properties that can be obtained from a zero-knowledge protocol. Pass showed that in the common reference string model non-interactive zero-knowledge protocols do not preserve all of the properties of interactive zero-knowledge protocols, e.g. they do not preserve deniability.
Non-interactive zero-knowledge proofs can also be obtained in the random oracle model using the Fiat-Shamir heuristic
Fiat-Shamir heuristic
Fiat and Shamir showed a major application of random oracles - the removal of interaction from protocols for the creation of signatures....
.
Definition
Originally, non-interactive zero-knowledge was only defined as a single theorem proof system. In such a system each proof requires its own fresh common reference string.A common reference string in general is not a random string. It may, for instance, consist of randomly chosen group elements that all protocol parties use. Although the group elements are random, the reference string is not as it contains a certain structure (e.g., group elements) that is distinguishable from randomness.
Subsequently, Feige, Lapidot, and Shamir
Adi Shamir
Adi Shamir is an Israeli cryptographer. He is a co-inventor of the RSA algorithm , a co-inventor of the Feige–Fiat–Shamir identification scheme , one of the inventors of differential cryptanalysis and has made numerous contributions to the fields of cryptography and computer...
introduced multi-theorem zero-knowledge proofs as a more versatile notion for non-interactive zero knowledge proofs.
In this model the prover and the verifier are in possession of a reference string sampled from a distribution D by a trusted setup
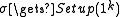. To prove statement 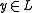with witness w, the prover runs 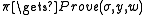and sends the proof to the verifier. The verifier accepts if , and rejects otherwise.To account for the fact that
may influence the statements that are being proven, the witness relation can begeneralized to
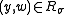parameterized by.Completeness
Verification succeeds for all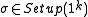 and every .More formally, for all k, all
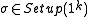, and all :
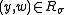Soundness
Soundness requires that no prover can make the verifier accept for a wrong statement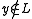 except with some small probability. The upper bound of this probability is referred to as the soundness error of a proof system.More formally, for every malicious prover
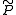, there exists a negligible function such that-
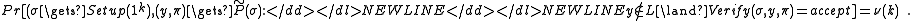
The above definition requires the soundness error to be negligible in the security parameter k. By increasing k the soundness error can be made arbitrary small. If the soundness error is 0 for all k, we speak of perfect soundness.
Multi-theorem Zero-knowledge
A non-interactive proof system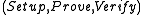
is multi-theorem zero-knowledge, if there exists a simulator 
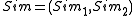such that for all non-uniform polynomial time adversaries 
,
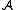Here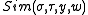
outputs 
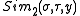for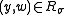 
and both oracles output failure otherwise.
Pairing-based Non-interactive Proofs
Pairing-based cryptographyPairing-based cryptographyPairing-based cryptography is the use of a pairing between elements of two cryptographic groups to a third group to construct cryptographic systems. If the same group is used for the first two groups, the pairing is called symmetric and is a mapping from two elements of one group to an element from...
has led to several cryptographic advancements. One of this advancements are more powerful and more efficient non-interactive zero-knowledge proofs. The seminal idea was to hide the values for the evaluation of the pairing in a commitmentCommitment schemeIn cryptography, a commitment scheme allows one to commit to a value while keeping it hidden, with the ability to reveal the committed value later. Commitments are used to bind a party to a value so that they cannot adapt to other messages in order to gain some kind of inappropriate advantage...
. Using different commitment schemes, this idea was used to build zero-knowledge proof systems under the sub-group hidingSub-group hidingThe sub-group hiding assumption is a computational hardness assumption used in elliptic curve cryptography and pairing-based cryptography.It was first introduced in to build a 2-DNF homomorphic encryption scheme....
and under the decisional linear assumptionDecisional Linear assumptionThe Decision Linear assumption is a mathematical assumption used in elliptic curve cryptography. In particular, the DLIN assumption is useful in settings where the decisional Diffie–Hellman assumption does not hold...
. These proof systems prove circuite satisfiabilityBoolean satisfiability problemIn computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
, and thus by the Cook–Levin theorem allow to prove membership for every language in NP. The size of the common reference string and the proofs is relatively small, however transforming a statement into a boolean circuit causes a considerable overhead.
Proof systems under the sub-group hidingSub-group hidingThe sub-group hiding assumption is a computational hardness assumption used in elliptic curve cryptography and pairing-based cryptography.It was first introduced in to build a 2-DNF homomorphic encryption scheme....
, decisional linear assumptionDecisional Linear assumptionThe Decision Linear assumption is a mathematical assumption used in elliptic curve cryptography. In particular, the DLIN assumption is useful in settings where the decisional Diffie–Hellman assumption does not hold...
, and external Diffie-Hellman assumptionXDH AssumptionThe external Diffie–Hellman assumption is a mathematic assumption used in elliptic curve cryptography. The XDH assumption holds that there exist certain subgroups of elliptic curves which have useful properties for cryptography...
that allow to directly proof the pairing product equations that are common in Pairing-based cryptographyPairing-based cryptographyPairing-based cryptography is the use of a pairing between elements of two cryptographic groups to a third group to construct cryptographic systems. If the same group is used for the first two groups, the pairing is called symmetric and is a mapping from two elements of one group to an element from...
have been proposed.
External links
-
