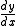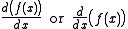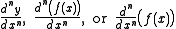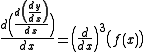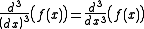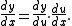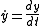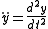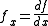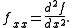Notation for differentiation
Encyclopedia
In differential calculus
, there is no single uniform notation for differentiation. Instead, several different notations for the derivative
of a function
or variable have been proposed by different mathematicians. The usefulness of each notation varies with the context, and it is sometimes advantageous to use more than one notation in a given context. The most common notations for differentiation are listed below.
is used throughout mathematics. It is particularly common when the equation
y = f(x) is regarded as a functional relationship between dependent and independent variables
y and x. In this case the derivative can be written as:
The function whose value at x is the derivative of f at x is therefore written
(although strictly speaking this denotes the variable value of the derivative function rather than the derivative function itself).
Higher derivatives are expressed as
for the nth derivative of y = f(x). Historically, this came from the fact that, for example, the third derivative is:
which we can loosely write (dropping the brackets in the denominator) as:
as above.
With Leibniz's notation, the value of derivative of y at a point x = a can be written in two different ways:
Leibniz's notation allows one to specify the variable for differentiation (in the denominator). This is especially helpful when considering partial derivative
s. It also makes the chain rule
easy to remember and recognize:
In the formulation of calculus in terms of limits, the du symbol has been assigned various meanings by various authors.
Some authors do not assign a meaning to du by itself, but only as part of the symbol du/dx.
Others define dx as an independent variable, and use d(x + y) = dx + dy and d(x·y) = dx·y + x·dy as formal axiom
s for differentiation. See differential algebra
.
In non-standard analysis
du is defined as an infinitesimal.
It is also interpreted as the exterior derivative
du of a function u.
See differential (infinitesimal) for further information.
and uses the prime mark
:
the first three derivatives of f are denoted
After this, some authors continue by employing Roman numerals such as f IV for the fourth derivative of f, while others put the number of derivatives in brackets, so that the fourth derivative of f would be denoted f (4). The latter notation extends readily to any number of derivatives, so that the nth derivative of f is denoted f (n).
's notation uses a differential operator
, denoted as D, which is prefixed to the function so that the derivatives of a function f are denoted by
When taking the derivative of a dependent variable y = f(x) it is common to add the independent variable x as a subscript to the D notation, leading to the alternative notation
If there is only one independent variable present, the subscript to the operator is usually dropped, however.
Euler's notation is useful for stating and solving linear differential equation
s.
and so on. It can also be used as a direct substitute for the prime in Lagrange's notation. Again this is common for functions f(t) of time.
Newton's notation is mainly used in mechanics
and the theory of ordinary differential equation
s. It is usually only used for first and second derivatives, and then, only to denote derivatives with respect to time.
and integration
of vector
or scalar fields particularly in a three-dimensional Euclidean space
, and uses specific notations of differentiation. In a Cartesian coordinate o-xyz, assuming a vector field
A is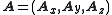
, and a scalar field
is 
.
First, a differential operator, or a Hamilton operator ∇
which is called del
is symbolically defined in a form of a vector,
,
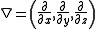where the terminology symbolically reflects that the operator ∇ will also be treated as an ordinary vector.
,
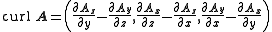Differential calculus
In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
, there is no single uniform notation for differentiation. Instead, several different notations for the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
or variable have been proposed by different mathematicians. The usefulness of each notation varies with the context, and it is sometimes advantageous to use more than one notation in a given context. The most common notations for differentiation are listed below.
Leibniz's notation
The original notation employed by Gottfried LeibnizGottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
is used throughout mathematics. It is particularly common when the equation
y = f(x) is regarded as a functional relationship between dependent and independent variables
Dependent and independent variables
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
y and x. In this case the derivative can be written as:
The function whose value at x is the derivative of f at x is therefore written
(although strictly speaking this denotes the variable value of the derivative function rather than the derivative function itself).
Higher derivatives are expressed as
for the nth derivative of y = f(x). Historically, this came from the fact that, for example, the third derivative is:
which we can loosely write (dropping the brackets in the denominator) as:
as above.
With Leibniz's notation, the value of derivative of y at a point x = a can be written in two different ways:
Leibniz's notation allows one to specify the variable for differentiation (in the denominator). This is especially helpful when considering partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s. It also makes the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
easy to remember and recognize:
In the formulation of calculus in terms of limits, the du symbol has been assigned various meanings by various authors.
Some authors do not assign a meaning to du by itself, but only as part of the symbol du/dx.
Others define dx as an independent variable, and use d(x + y) = dx + dy and d(x·y) = dx·y + x·dy as formal axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s for differentiation. See differential algebra
Differential algebra
In mathematics, differential rings, differential fields, and differential algebras are rings, fields, and algebras equipped with a derivation, which is a unary function that is linear and satisfies the Leibniz product law...
.
In non-standard analysis
Non-standard analysis
Non-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...
du is defined as an infinitesimal.
It is also interpreted as the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
du of a function u.
See differential (infinitesimal) for further information.
Lagrange's notation
One of the most common modern notations for differentiation is due to Joseph Louis LagrangeJoseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
and uses the prime mark
Prime (symbol)
The prime symbol , double prime symbol , and triple prime symbol , etc., are used to designate several different units, and for various other purposes in mathematics, the sciences and linguistics...
:
the first three derivatives of f are denoted
-
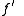for the first derivative,
-
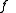for the second derivativeSecond derivativeIn calculus, the second derivative of a function ƒ is the derivative of the derivative of ƒ. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of a vehicle with respect to time is...
,
-
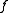for the third derivative.
After this, some authors continue by employing Roman numerals such as f IV for the fourth derivative of f, while others put the number of derivatives in brackets, so that the fourth derivative of f would be denoted f (4). The latter notation extends readily to any number of derivatives, so that the nth derivative of f is denoted f (n).
Euler's notation
EulerLeonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
's notation uses a differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
, denoted as D, which is prefixed to the function so that the derivatives of a function f are denoted by
-
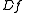for the first derivative,
-
for the second derivative, and
-
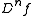for the nth derivative, for any positive integer n.
When taking the derivative of a dependent variable y = f(x) it is common to add the independent variable x as a subscript to the D notation, leading to the alternative notation
-
for the first derivative,
-
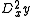for the second derivative, and
-
for the nth derivative, for any positive integer n.
If there is only one independent variable present, the subscript to the operator is usually dropped, however.
Euler's notation is useful for stating and solving linear differential equation
Linear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
s.
Newton's notation
Newton's notation for differentiation (also called the dot notation for differentiation) requires placing a dot over the dependent variable and is often used for time derivatives such as velocity and acceleration:
and so on. It can also be used as a direct substitute for the prime in Lagrange's notation. Again this is common for functions f(t) of time.
Newton's notation is mainly used in mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
and the theory of ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s. It is usually only used for first and second derivatives, and then, only to denote derivatives with respect to time.
Notation in vector calculus
Vector calculus concerns differentiationDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
and integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of vector
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
or scalar fields particularly in a three-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, and uses specific notations of differentiation. In a Cartesian coordinate o-xyz, assuming a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
A is
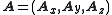, and a scalar fieldScalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
is .First, a differential operator, or a Hamilton operator ∇
Nabla symbol
right|thumb|256px|The [[harp]], the instrument after which the nabla symbol is namedNabla is the symbol \nabla . The name comes from the Greek word for a Hebrew harp, which had a similar shape. Related words also exist in Aramaic and Hebrew. The symbol was first used by William Rowan Hamilton in...
which is called del
Del
In vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
is symbolically defined in a form of a vector,
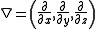,where the terminology symbolically reflects that the operator ∇ will also be treated as an ordinary vector.
- GradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
: The gradient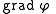
of the scalar field 
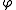is a vector, which is symbolically expressed by the multiplicationMultiplicationMultiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
of ∇ and scalar field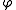
,
-
,
-
-
-
,
-
-
-
-
-
.
-
-
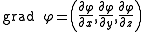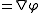- DivergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
: The divergence
of the vector A is a scalar, which is symbolically expressed by the dot productDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of ∇ and the vector A,
-
,
-
-
-
,
-
-
-
-
-
.
-
-
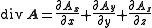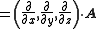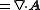- Laplacian: The Laplacian
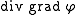of the scalar field 
is a scalar, which is symbolically expressed by the scalar multiplication of ∇2 and the scalar field φ,
-
-
-
-
,
-
-
-
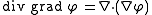
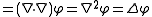- where,
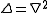is called a Laplacian operator.
- Rotation: The rotation
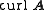, or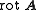 
, of the vector is a vector, which is symbolically expressed by the cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of ∇ and the vector A,
,-
-
,
-
-
-
,
-
-
.
-
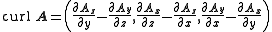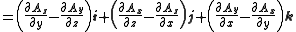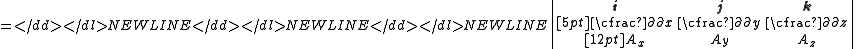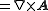Many symbolic operations of derivatives can be generalized in a straightforward manner by the gradient operator in Cartesian coordinates. For example, the single-variable product ruleProduct ruleIn calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
has a direct analogue in the multiplication of scalar fields by applying the gradient operator, as in
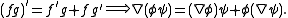
Further notations have been developed for more exotic types of spaces. For calculations in Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, the D'Alembert operatorD'Alembert operatorIn special relativity, electromagnetism and wave theory, the d'Alembert operator , also called the d'Alembertian or the wave operator, is the Laplace operator of Minkowski space. The operator is named for French mathematician and physicist Jean le Rond d'Alembert...
, also called the D'Alembertian, wave operator, or box operator is represented as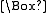
, or as 
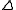when not in conflict with the symbol for the Laplacian.
Other notations
When more specific types of differentiation are necessary, such as in multivariate calculus or tensor analysis, other notations are common.
For a function f(x), we can express the derivative using subscripts of the independent variable:
This is especially useful for taking partial derivatives of a function of several variables.
Partial derivatives will generally be distinguished from ordinary derivatives by replacing the differential operator d with a "∂" symbol. For example, we can indicate the partial derivative of f(x,y,z) with respect to x, but not to y or z in several ways:
where the final two notations are equivalent in flat Euclidean SpaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
but are different in other manifolds.
Other generalizations of the derivative can be found in various subfields of mathematics, physics, and engineering.
External links
- Earliest Uses of Symbols of Calculus, maintained by Jeff Miller.
-
-
