In communications, the Nyquist ISI criterion describes the conditions which, when satisfied by a communication channel

Channel (communications)

In telecommunications and computer networking, a communication channel, or channel, refers either to a physical transmission medium such as a wire, or to a logical connection over a multiplexed medium such as a radio channel...

, result in no intersymbol interference

Intersymbol interference

In telecommunication, intersymbol interference is a form of distortion of a signal in which one symbol interferes with subsequent symbols. This is an unwanted phenomenon as the previous symbols have similar effect as noise, thus making the communication less reliable...

 or ISI. It provides a method for constructing band-limited functions to overcome the effects of intersymbol interference.

When consecutive symbols are transmitted over a channel by a linear modulation (such as ASK

Amplitude-shift keying

Amplitude-shift keying is a form of modulation that represents digital data as variations in the amplitude of a carrier wave.Any digital modulation scheme uses a finite number of distinct signals to represent digital data. ASK uses a finite number of amplitudes, each assigned a unique pattern of...

, QAM

Quadrature amplitude modulation

Quadrature amplitude modulation is both an analog and a digital modulation scheme. It conveys two analog message signals, or two digital bit streams, by changing the amplitudes of two carrier waves, using the amplitude-shift keying digital modulation scheme or amplitude modulation analog...

, etc.), the impulse response

Impulse response

In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...

 (or equivalently the frequency response

Frequency response

Frequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input...

) of the channel causes a transmitted symbol to be spread in the time domain. This causes intersymbol interference because the previously transmitted symbols affect the currently received symbol, thus reducing tolerance for noise

Noise

In common use, the word noise means any unwanted sound. In both analog and digital electronics, noise is random unwanted perturbation to a wanted signal; it is called noise as a generalisation of the acoustic noise heard when listening to a weak radio transmission with significant electrical noise...

. The Nyquist theorem relates this time-domain condition to an equivalent frequency-domain condition.

The Nyquist criterion is closely related to the Nyquist-Shannon sampling theorem, with only a differing point of view.

Nyquist criterion

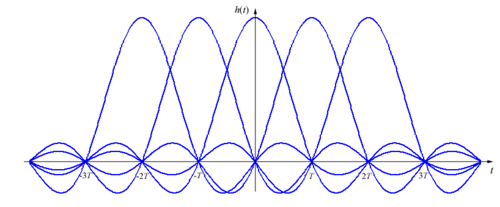
If we denote the channel impulse response as , then the condition for an ISI-free response can be expressed as: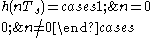


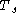for all integers , where is the symbol period. The Nyquist theorem says that this is equivalent to:
,

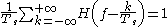where is the Fourier transform

Fourier transform

In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...

 of 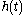. This is the Nyquist ISI criterion.

This criterion can be intuitively understood in the following way: frequency-shifted replicas of H(f) must add up to a constant value.

In practice this criterion is applied to baseband filtering by regarding the symbol sequence as weighted impulses (Dirac delta function

Dirac delta function

The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...

). When the baseband filters in the communication system satisfy the Nyquist criterion, symbols can be transmitted over a channel with flat response within a limited frequency band, without ISI. Examples of such baseband filters are the raised-cosine filter

Raised-cosine filter

The raised-cosine filter is a filter frequently used for pulse-shaping in digital modulation due to its ability to minimise intersymbol interference...

, or the sinc filter

Sinc filter

In signal processing, a sinc filter is an idealized filter that removes all frequency components above a given bandwidth, leaves the low frequencies alone, and has linear phase...

 as the ideal case.

Derivation

To derive the criterion, we first express the received signal in terms of the transmitted symbol and the channel response. Let the function h(t) be the channel impulse response

Impulse response

In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...

, x[n] the symbols to be sent, with a symbol period of T_s; the received signal y(t) will be in the form (where noise has been ignored for simplicity):
.

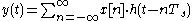Sampling this signal at intervals of T_s, we can express y(t) as a discrete-time equation:
.

If we write the h[0] term of the sum separately, we can express this as:
,

and from this we can conclude that if a response h[n] satisfies
,

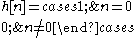only one transmitted symbol has an effect on the received y[k] at sampling instants, thus removing any ISI. This is the time-domain condition for an ISI-free channel. Now we find a frequency-domain equivalent for it. We start by expressing this condition in continuous time:


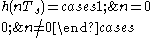
for all integer . We multiply such a h(t) by a sum of Dirac delta function

Dirac delta function

The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...

 (impulses) separated by intervals T_s This is equivalent of sampling the response as above but using a continuous time expression. The right side of the condition can then be expressed as one impulse in the origin:


Fourier transforming both members of this relationship we obtain:


and
.

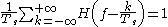This is the Nyquist ISI criterion and, if a channel response satisfies it, then there is no ISI between the different samples.

See also

• Intersymbol interference
  Intersymbol interference
  In telecommunication, intersymbol interference is a form of distortion of a signal in which one symbol interferes with subsequent symbols. This is an unwanted phenomenon as the previous symbols have similar effect as noise, thus making the communication less reliable...
  
  
• Nyquist rate
  Nyquist rate
  In signal processing, the Nyquist rate, named after Harry Nyquist, is two times the bandwidth of a bandlimited signal or a bandlimited channel...
  
  
• Nyquist-Shannon sampling theorem
• Pulse shaping
  Pulse shaping
  In digital telecommunication, pulse shaping is the process of changing the waveform of transmitted pulses. Its purpose is to make the transmitted signal better suited to the communication channel by limiting the effective bandwidth of the transmission. By filtering the transmitted pulses this way,...
  
  
• Raised-cosine filter
  Raised-cosine filter
  The raised-cosine filter is a filter frequently used for pulse-shaping in digital modulation due to its ability to minimise intersymbol interference...