
O-minimal theory
Encyclopedia
In mathematical logic
, and more specifically in model theory
, an infinite structure
(M,<,...) which is totally ordered
by < is called an o-minimal structure if and only if every definable
subset X ⊂ M (with parameters taken from M) is a finite union
of interval
s and points.
O-minimality can be regarded as a weak form of quantifier elimination
. A structure M is o-minimal if and only if every formula with one free variable and parameters in M is equivalent to a quantifier-free formula involving only the ordering, also with parameters in M. This is analogous to the minimal
structures, which are exactly the analogous property down to equality.
A theory
T is an o-minimal theory if every model
of T is o-minimal. Pillay can show that the complete theory T of an o-minimal structure is an o-minimal theory. This result is remarkable because the complete theory of a minimal structure need not be a strongly minimal theory
, that is, there may be an elementarily equivalent structure which is not minimal.
If M has a dense linear order without endpoints on it, say <, then a structure S on M is called o-minimal if it satisfies the extra axioms
The "o" stands for "order", since any o-minimal structure requires an ordering on the underlying set.
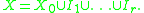
In the first example, the definable sets are the semialgebraic set
s. Thus the study of o-minimal structures and theories generalises Real algebraic geometry
. A major line of current research is based on discovering expansions of the real ordered field that are o-minimal. Despite the generality of application, one can show a great deal about the geometry of set definable in o-minimal structures. There is a cell decomposition theorem, Whitney
and Verdier
stratification
theorems and a good notion of dimension and Euler characteristic.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, and more specifically in model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, an infinite structure
Structure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
(M,<,...) which is totally ordered
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
by < is called an o-minimal structure if and only if every definable
Definable set
In mathematical logic, a definable set is an n-ary relation on the domain of a structure whose elements are precisely those elements satisfying some formula in the language of that structure...
subset X ⊂ M (with parameters taken from M) is a finite union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
s and points.
O-minimality can be regarded as a weak form of quantifier elimination
Quantifier elimination
Quantifier elimination is a concept of simplification used in mathematical logic, model theory, and theoretical computer science. One way of classifying formulas is by the amount of quantification...
. A structure M is o-minimal if and only if every formula with one free variable and parameters in M is equivalent to a quantifier-free formula involving only the ordering, also with parameters in M. This is analogous to the minimal
Strongly minimal theory
In model theory—a branch of mathematical logic—a minimal structure is an infinite one-sorted structure such that every subset of its domain that is definable with parameters is either finite or cofinite. A strongly minimal theory is a complete theory all models of that are minimal...
structures, which are exactly the analogous property down to equality.
A theory
Theory (mathematical logic)
In mathematical logic, a theory is a set of sentences in a formal language. Usually a deductive system is understood from context. An element \phi\in T of a theory T is then called an axiom of the theory, and any sentence that follows from the axioms is called a theorem of the theory. Every axiom...
T is an o-minimal theory if every model
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of T is o-minimal. Pillay can show that the complete theory T of an o-minimal structure is an o-minimal theory. This result is remarkable because the complete theory of a minimal structure need not be a strongly minimal theory
Strongly minimal theory
In model theory—a branch of mathematical logic—a minimal structure is an infinite one-sorted structure such that every subset of its domain that is definable with parameters is either finite or cofinite. A strongly minimal theory is a complete theory all models of that are minimal...
, that is, there may be an elementarily equivalent structure which is not minimal.
Set-theoretic definition
O-minimal structures can be defined without recourse to model theory. Here we define a structure on a nonempty set M in a set-theoretic manner, as a sequence S = (Sn), n = 0,1,2,... such that- Sn is a boolean algebra of subsets of Mn
- if A ∈ Sn then M × A and A ×M are in Sn+1
- the set {(x1,...,xn) ∈ Mn : x1 = xn} is in Sn
- if A ∈ Sn+1 and π : Mn+1 → Mn is the projection map on the first n coordinates, then π(A) ∈ Mn.
If M has a dense linear order without endpoints on it, say <, then a structure S on M is called o-minimal if it satisfies the extra axioms
- the set {(x,y) ∈ M2 : x < y} is in S2
- the sets in S1 are precisely the finite unions of intervals and points.
The "o" stands for "order", since any o-minimal structure requires an ordering on the underlying set.
Model theoretic definition
O-minimal structures originated in model theory and so have a simpler — but equivalent — definition using the language of model theory. Specifically if L is a language including a binary relation <, and (M,<,...) is an L-structure where < is interpreted to satisfy the axioms of a dense linear order, then (M,<,...) is called an o-minimal structure if for any definable set X ⊆ M there are finitely many intervals I1,...,Ir with endpoints in M ∪ {±∞} and a finite set X0 such that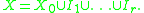
Examples
Examples of o-minimal theories are:- RCF, the theoryTheoryThe English word theory was derived from a technical term in Ancient Greek philosophy. The word theoria, , meant "a looking at, viewing, beholding", and referring to contemplation or speculation, as opposed to action...
of real closed fieldReal closed fieldIn mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
s; - The complete theoryComplete theoryIn mathematical logic, a theory is complete if it is a maximal consistent set of sentences, i.e., if it is consistent, and none of its proper extensions is consistent...
of the real fieldReal fieldReal field may refer to:* Real numbers, the numbers that can be represented by infinite decimals* Formally real field, an algebraic field that has the so-called "real" property* Realfield, a spoof of Garfield...
with a symbol for the exponential functionExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
by Wilkie's theoremWilkie's theoremIn mathematics, Wilkie's theorem is a result by Alex Wilkie about the theory of ordered fields with an exponential function, or equivalently about the geometric nature of exponential varieties.-Formulations:...
; - The complete theory of the real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s with restricted analytic functionAnalytic functionIn mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s added (i.e. analytic functions on a neighborhood of [0,1]n, restricted to [0,1]n; note that the unrestricted sine function has infinitely many roots, and so cannot be definable in a o-minimal structure.) - Intermediate to the previous two examples is the complete theory of the real numbers with restricted Pfaffian functionPfaffian functionIn mathematics, the Pfaffian functions are a certain class of functions introduced by Askold Georgevich Khovanskiǐ in the 1970s. They are named after German mathematician Johann Pfaff.-Basic definition:...
s added. - The complete theory of dense linear orders in the language with just the ordering.
In the first example, the definable sets are the semialgebraic set
Semialgebraic set
In mathematics, a semialgebraic set is a subset S of Rn for some real closed field R defined by a finite sequence of polynomial equations and inequalities , or any finite union of such sets. A semialgebraic function is a function with semialgebraic graph...
s. Thus the study of o-minimal structures and theories generalises Real algebraic geometry
Real algebraic geometry
In mathematics, real algebraic geometry is the study of real algebraic sets, i.e. real-number solutions to algebraic equations with real-number coefficients, and mappings between them ....
. A major line of current research is based on discovering expansions of the real ordered field that are o-minimal. Despite the generality of application, one can show a great deal about the geometry of set definable in o-minimal structures. There is a cell decomposition theorem, Whitney
Hassler Whitney
Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
and Verdier
Jean-Louis Verdier
Jean-Louis Verdier was a French mathematician who worked, under the guidance of Alexander Grothendieck, on derived categories and Verdier duality...
stratification
Stratification (mathematics)
-In mathematical logic:In mathematical logic, stratification is any consistent assignment of numbers to predicate symbols guaranteeing that a unique formal interpretation of a logical theory exists...
theorems and a good notion of dimension and Euler characteristic.
See also
- Semialgebraic setSemialgebraic setIn mathematics, a semialgebraic set is a subset S of Rn for some real closed field R defined by a finite sequence of polynomial equations and inequalities , or any finite union of such sets. A semialgebraic function is a function with semialgebraic graph...
- Real algebraic geometryReal algebraic geometryIn mathematics, real algebraic geometry is the study of real algebraic sets, i.e. real-number solutions to algebraic equations with real-number coefficients, and mappings between them ....
- Strongly minimal theoryStrongly minimal theoryIn model theory—a branch of mathematical logic—a minimal structure is an infinite one-sorted structure such that every subset of its domain that is definable with parameters is either finite or cofinite. A strongly minimal theory is a complete theory all models of that are minimal...
- Weakly o-minimal structureWeakly o-minimal structureIn model theory, a weakly o-minimal structure is a model theoretic structure whose definable sets in the domain are just finite unions of convex sets.-Definition:A linearly ordered structure, M, with language L including an ordering relation...
- C-minimal theoryC-minimal theoryIn model theory, a branch of mathematical logic, a C-minimal theory is a theory that is "minimal" with respect to a ternary relation C with certain properties...

