
Occurrences of Grandi's series
Encyclopedia
Parables
Guido GrandiGuido Grandi
thumb|Guido GrandiDom Guido Grandi, O.S.B. Cam., was an Italian monk, priest, philosopher, mathematician, and engineer.-Life:...
illustrated the series with a parable involving two brothers who share a gem.
Thomson's lamp
Thomson's lamp
Thomson's lamp is a puzzle that is a variation on Zeno's paradoxes. It was devised by philosopher James F. Thomson, who also coined the term supertask....
is a supertask
Supertask
In philosophy, a supertask is a quantifiably infinite number of operations that occur sequentially within a finite interval of time. Supertasks are called "hypertasks" when the number of operations becomes innumerably infinite. The term supertask was coined by the philosopher James F...
in which a hypothetical lamp is turned on and off infinitely many times in a finite time span. One can think of turning the lamp on as adding 1 to its state, and turning it off as subtracting 1. Instead of asking the sum of the series, one asks the final state of the lamp.
One of the best-known classic parables to which infinite series have been applied, Achilles and the tortoise, can also be adapted to the case of Grandi's series.
Numerical series
The Cauchy product of Grandi's series with itself is 1 − 2 + 3 − 4 + · · ·.Several series resulting from the introduction of zeros into Grandi's series have interesting properties; for these see Summation of Grandi's series#Dilution.
Grandi's series is just one example of a divergent geometric series.
The rearranged series 1 − 1 − 1 + 1 + 1 − 1 − 1 + · · · occurs in Euler's 1775 treatment of the pentagonal number theorem as the value of the Euler function at q = 1.
Power series
The power series most famously associated with Grandi's series is its ordinary generating function,
Hyperbolic sine
In his 1822 Théorie Analytique de la Chaleur, Joseph FourierJoseph Fourier
Jean Baptiste Joseph Fourier was a French mathematician and physicist best known for initiating the investigation of Fourier series and their applications to problems of heat transfer and vibrations. The Fourier transform and Fourier's Law are also named in his honour...
obtains what we now call a Fourier sine series for a scaled version of the hyperbolic sine function,

He finds that the general coefficient of sin nx in the series is

For n > 1 the above series converges, while the coefficient of sin x appears as 1 − 1 + 1 − 1 + · · · and so is expected to be 1⁄2. In fact, this is correct, as can be demonstrated by directly calculating the Fourier coefficient from an integral:
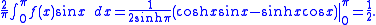
Dirac comb
Grandi's series occurs more directly in another important series,
At x = π, the series reduces to −1 + 1 − 1 + 1 − · · · and so one might expect it to meaningfully equal −1⁄2. In fact, Euler held that this series obeyed the formal relation Σ cos kx = −1⁄2, while d'Alembert rejected the relation, and Lagrange wondered if it could be defended by an extension of the geometric series similar to Euler's reasoning with Grandi's numerical series.
Euler's claim suggests that
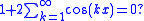
for all x. This series is divergent everywhere, while its Cesaro sum is indeed 0 for almost all x. However, the series diverges to infinity at x = 2πn in a significant way: it is the Fourier series of a Dirac comb
Dirac comb
In mathematics, a Dirac comb is a periodic Schwartz distribution constructed from Dirac delta functions...
. The ordinary, Cesaro, and Abel sums of this series involve limits of the Dirichlet, Fejér, and Poisson kernel
Poisson kernel
In potential theory, the Poisson kernel is an integral kernel, used for solving the two-dimensional Laplace equation, given Dirichlet boundary conditions on the unit disc. The kernel can be understood as the derivative of the Green's function for the Laplace equation...
s, respectively.
Dirichlet series
Multiplying the terms of Grandi's series by 1/nz yields the Dirichlet series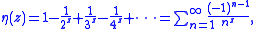
which converges only for complex numbers z with a positive real part. Grandi's series is recovered by letting z = 0.
Unlike the geometric series, the Dirichlet series for η is not useful for determining what 1 − 1 + 1 − 1 + · · · "should" be. Even on the right half-plane, η(z) is not given by any elementary expression, and there is no immediate evidence of its limit as z approaches 0. On the other hand, if one uses stronger methods of summability, then the Dirichlet series for η defines a function on the whole complex plane — the Dirichlet eta function — and moreover, this function is analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
. For z with real part > −1 it suffices to use Cesaro summation, and so η(0) = 1⁄2 after all.
The function η is related to a more famous Dirichlet series and function:

where ζ is the Riemann zeta function. Keeping Grandi's series in mind, this relation explains why ζ(0) = −1⁄2; see also 1 + 1 + 1 + 1 + · · ·. The relation also implies a much more important result. Since η(z) and (1 − 21−z) are both analytic on the entire plane and the latter function's only zero
Zero (complex analysis)
In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
is a simple zero at z = 1, it follows that ζ(z) is meromorphic
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
with only a simple pole at z = 1.
Euler characteristics
Given a CW complexCW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
S containing one vertex, one edge, one face, and generally exactly one cell of every dimension, Euler's formula for the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of S returns . There are a few motivations for defining a generalized Euler characteristic for such a space that turns out to be 1/2.
One approach comes from combinatorial geometry. The open interval (0, 1) has an Euler characteristic of −1, so its power set 2(0, 1) should have an Euler characteristic of 2−1 = 1/2. The appropriate power set to take is the "small power set" of finite subsets of the interval, which consists of the union of a point (the empty set), an open interval (the set of singetons), an open triangle, and so on. So the Euler characteristic of the small power set is . James Propp defines a regularized Euler measure for polyhedral sets that, in this example, replaces with , sums the series for |t| < 1, and analytically continues to t = 1, essentially finding the Abel sum of , which is 1/2. Generally, he finds χ(2A) = 2χ(A) for any polyhedral set A, and the base of the exponent generalizes to other sets as well.
Infinite-dimensional real projective space
Real projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
RP∞ is another structure with one cell of every dimension and therefore an Euler characteristic of . This space can be described as the quotient of the infinite-dimensional sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
by identifying each pair of antipodal point
Antipodal point
In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....
s. Since the infinite-dimensional sphere is contractible, its Euler characteristic is 1, and its 2-to-1 quotient should have an Euler characteristic of 1/2.
This description of RP∞ also makes it the classifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
of Z2, the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order 2. Tom Leinster gives a definition of the Euler characteristic of any category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
which bypasses the classifying space and reduces to 1/|G| for any group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
when viewed as a one-object category. In this sense the Euler characteristic of Z2 is itself 1⁄2.
In physics
Grandi's series, and generalizations thereof, occur frequently in many branches of physics; most typically in the discussions of quantized fermionFermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
fields (for example, the chiral bag model), which have both positive and negative eigenvalues; although similar series occur also for boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s, such as in the Casimir effect
Casimir effect
In quantum field theory, the Casimir effect and the Casimir–Polder force are physical forces arising from a quantized field. The typical example is of two uncharged metallic plates in a vacuum, like capacitors placed a few micrometers apart, without any external electromagnetic field...
.
The general series is discussed in greater detail in the article on spectral asymmetry
Spectral asymmetry
In mathematics and physics, the spectral asymmetry is the asymmetry in the distribution of the spectrum of eigenvalues of an operator. In mathematics, the spectral asymmetry arises in the study of elliptic operators on compact manifolds, and is given a deep meaning by the Atiyah-Singer index theorem...
, whereas methods used to sum it are discussed in the articles on regularization
Regularization (physics)
-Introduction:In physics, especially quantum field theory, regularization is a method of dealing with infinite, divergent, and non-sensical expressions by introducing an auxiliary concept of a regulator...
and, in particular, the zeta function regulator.

