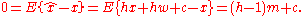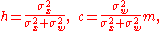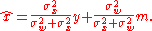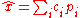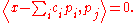Orthogonality principle
Encyclopedia
In statistics
and signal processing
, the orthogonality principle is a necessary and sufficient condition for the optimality of a Bayesian estimator. Loosely stated, the orthogonality principle says that the error vector of the optimal estimator (in a mean square error sense) is orthogonal to any possible estimator. The orthogonality principle is most commonly stated for linear estimators, but more general formulations are possible. Since the principle is a necessary and sufficient condition for optimality, it can be used to find the minimum mean square error estimator.
 for some matrix H and vector c. Then, the orthogonality principle states that an estimator
for some matrix H and vector c. Then, the orthogonality principle states that an estimator  achieves minimum mean square error if and only if
achieves minimum mean square error if and only if
If x and y have zero mean, then it suffices to require the first condition.
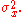 Also suppose we observe a value
Also suppose we observe a value 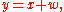 where w is Gaussian noise which is independent of x and has mean 0 and variance
where w is Gaussian noise which is independent of x and has mean 0 and variance 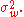 We wish to find a linear estimator
We wish to find a linear estimator 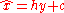 minimizing the MSE. Substituting the expression
minimizing the MSE. Substituting the expression 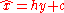 into the two requirements of the orthogonality principle, we obtain
into the two requirements of the orthogonality principle, we obtain
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, the orthogonality principle is a necessary and sufficient condition for the optimality of a Bayesian estimator. Loosely stated, the orthogonality principle says that the error vector of the optimal estimator (in a mean square error sense) is orthogonal to any possible estimator. The orthogonality principle is most commonly stated for linear estimators, but more general formulations are possible. Since the principle is a necessary and sufficient condition for optimality, it can be used to find the minimum mean square error estimator.
Orthogonality principle for linear estimators
The orthogonality principle is most commonly used in the setting of linear estimation. In this context, let x be an unknown random vector which is to be estimated based on the observation vector y. One wishes to construct a linear estimator for some matrix H and vector c. Then, the orthogonality principle states that an estimator
for some matrix H and vector c. Then, the orthogonality principle states that an estimator  achieves minimum mean square error if and only if
achieves minimum mean square error if and only if
-
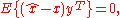 and
and -
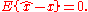
If x and y have zero mean, then it suffices to require the first condition.
Example
Suppose x is a Gaussian random variable with mean m and variance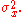 Also suppose we observe a value
Also suppose we observe a value 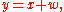 where w is Gaussian noise which is independent of x and has mean 0 and variance
where w is Gaussian noise which is independent of x and has mean 0 and variance 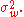 We wish to find a linear estimator
We wish to find a linear estimator 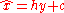 minimizing the MSE. Substituting the expression
minimizing the MSE. Substituting the expression 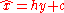 into the two requirements of the orthogonality principle, we obtain
into the two requirements of the orthogonality principle, we obtain
-

Solving these two linear equations for h and c results in
so that the linear minimum mean square error estimator is given by
This estimator can be interpreted as a weighted average between the noisy measurements y and the prior expected value m. If the noise variance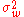 is low compared with the variance of the prior
is low compared with the variance of the prior 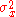 (corresponding to a high SNR), then most of the weight is given to the measurements y, which are deemed more reliable than the prior information. Conversely, if the noise variance is high relative to the prior variance, then the estimate will be close to m, as the measurements are not reliable enough to outweigh the prior information.
(corresponding to a high SNR), then most of the weight is given to the measurements y, which are deemed more reliable than the prior information. Conversely, if the noise variance is high relative to the prior variance, then the estimate will be close to m, as the measurements are not reliable enough to outweigh the prior information.
Finally, note that because the variables x and y are jointly Gaussian, the minimum MSE estimator is linear. Therefore, in this case, the estimator above minimizes the MSE among all estimators, not only linear estimators.
General formulation
Let be a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
be a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
of random variables with an inner product defined by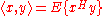 . Suppose
. Suppose  is a closedClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
is a closedClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
subspace of , representing the space of all possible estimators. One wishes to find a vector
, representing the space of all possible estimators. One wishes to find a vector  which will approximate a vector
which will approximate a vector  . More accurately, one would like to minimize the mean squared error (MSE)
. More accurately, one would like to minimize the mean squared error (MSE)  between
between  and
and  .
.
In the special case of linear estimators described above, the space is the set of all functions of
is the set of all functions of  and
and 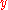 , while
, while  is the set of linear estimators, i.e., linear functions of
is the set of linear estimators, i.e., linear functions of 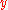 only. Other settings which can be formulated in this way include the subspace of causalCausal filterIn signal processing, a causal filter is a linear and time-invariant causal system. The word causal indicates that the filter output depends only on past and present inputs. A filter whose output also depends on future inputs is non-causal. A filter whose output depends only on future inputs is...
only. Other settings which can be formulated in this way include the subspace of causalCausal filterIn signal processing, a causal filter is a linear and time-invariant causal system. The word causal indicates that the filter output depends only on past and present inputs. A filter whose output also depends on future inputs is non-causal. A filter whose output depends only on future inputs is...
linear filters and the subspace of all (possibly nonlinear) estimators.
Geometrically, we can see this problem by the following simple case where is a one-dimensionalDimension (vector space)In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
is a one-dimensionalDimension (vector space)In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
subspace:
We want to find the closest approximation to the vector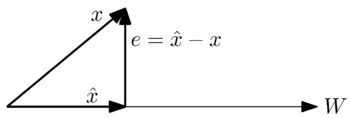
 by a vector
by a vector  in the space
in the space  . From the geometric interpretation, it is intuitive that the best approximation, or smallest error, occurs when the error vector,
. From the geometric interpretation, it is intuitive that the best approximation, or smallest error, occurs when the error vector,  , is orthogonal to vectors in the space
, is orthogonal to vectors in the space  .
.
More accurately, the general orthogonality principle states the following: Given a closed subspace of estimators within a Hilbert space
of estimators within a Hilbert space  and an element
and an element  in
in  , an element
, an element 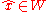 achieves minimum MSE among all elements in
achieves minimum MSE among all elements in  if and only if
if and only if 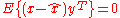 for all
for all 
Stated in such a manner, this principle is simply a statement of the Hilbert projection theoremHilbert projection theoremIn mathematics, the Hilbert projection theorem is a famous result of convex analysis that says that for every point x in a Hilbert space H and every closed convex C \subset H, there exists a unique point y \in C for which \lVert x - y \rVert is minimized over C....
. Nevertheless, the extensive use of this result in signal processing has resulted in the name "orthogonality principle."
A solution to error minimization problems
The following is one way to find the minimum mean square error estimator by using the orthogonality principle.
We want to be able to approximate a vector by
by
where
is the approximation of as a linear combination of vectors in the subspace
as a linear combination of vectors in the subspace  spanned by
spanned by 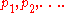 Therefore, we want to be able to solve for the coefficients,
Therefore, we want to be able to solve for the coefficients, 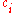 , so that we may write our approximation in known terms.
, so that we may write our approximation in known terms.
By the orthogonality theorem, the square norm of the error vector, , is minimized when, for all j,
, is minimized when, for all j,
Developing this equation, we obtain
-
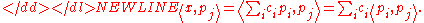
If there is a finite number of vectors
of vectors 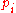 , one can write this equation in matrix form as
, one can write this equation in matrix form as
-
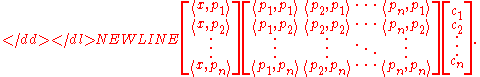
Assuming the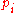 are linearly independent, the Gramian matrix can be inverted to obtain
are linearly independent, the Gramian matrix can be inverted to obtain
-
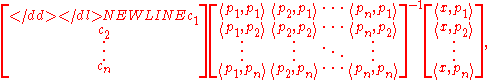
thus providing an expression for the coefficients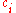 of the minimum mean square error estimator.
of the minimum mean square error estimator.
-
-
-