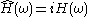Causal filter
Encyclopedia
In signal processing
, a causal filter is a linear and time-invariant
causal system
. The word causal indicates that the filter output depends only on past and present inputs. A filter
whose output also depends on future inputs is non-causal. A filter whose output depends only on future inputs is anti-causal
. Systems (including filters) that are realizable (i.e. that operate in real time
) must be causal because such systems cannot act on a future input. In effect that means the output sample that best represents the input at time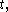
comes out slightly later. A common design practice is to create a realizable filter by shortening and/or time-shifting a non-causal impulse response. If shortening is necessary, it is often accomplished as the product of the impulse-response with a window function
.
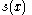. A constant factor of 1/2 is omitted for simplicity:
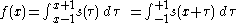
where x could represent a spatial coordinate, as in image processing. But if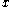
represents time 
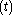, then a moving average defined that way is non-causal (also called non-realizable), because 
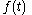depends on future inputs, such as 
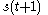. A realizable output is
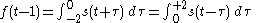
which is a delayed version of the non-realizable output.
Any linear filter (such as a moving average) can be characterized by a function h(t) called its impulse response
. Its output is the convolution
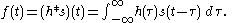
In those terms, causality requires
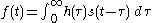
and general equality of these two expressions requires h(t) = 0 for all t < 0.
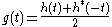
which is non-causal. On the other hand, g(t) is Hermitian and, consequently, its Fourier transform G(ω) is real-valued. We now have the following relation
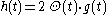
where Θ(t) is the Heaviside unit step function.
This means that the Fourier transforms of h(t) and g(t) are related as follows
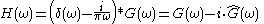
where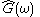
is a Hilbert transform
done in the frequency domain (rather than the time domain). The sign of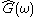
may depend on the definition of the Fourier Transform.
Taking the Hilbert transform of the above equation yields this relation between "H" and its Hilbert transform:
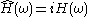
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, a causal filter is a linear and time-invariant
LTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
causal system
Causal system
A causal system is a system where the output depends on past/current inputs but not future inputs i.e...
. The word causal indicates that the filter output depends only on past and present inputs. A filter
Filter (signal processing)
In signal processing, a filter is a device or process that removes from a signal some unwanted component or feature. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal...
whose output also depends on future inputs is non-causal. A filter whose output depends only on future inputs is anti-causal
Anti-causal filter
In signal processing, an anti-causal system is one whose output depends only on present and future inputs. An anti-causal system that is also linear and time-invariant is an anti-causal filter...
. Systems (including filters) that are realizable (i.e. that operate in real time
Real-time computing
In computer science, real-time computing , or reactive computing, is the study of hardware and software systems that are subject to a "real-time constraint"— e.g. operational deadlines from event to system response. Real-time programs must guarantee response within strict time constraints...
) must be causal because such systems cannot act on a future input. In effect that means the output sample that best represents the input at time
comes out slightly later. A common design practice is to create a realizable filter by shortening and/or time-shifting a non-causal impulse response. If shortening is necessary, it is often accomplished as the product of the impulse-response with a window functionWindow function
In signal processing, a window function is a mathematical function that is zero-valued outside of some chosen interval. For instance, a function that is constant inside the interval and zero elsewhere is called a rectangular window, which describes the shape of its graphical representation...
.
Example
The following definition is a moving (or "sliding") average of input data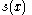. A constant factor of 1/2 is omitted for simplicity: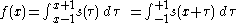where x could represent a spatial coordinate, as in image processing. But if
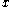represents time 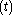, then a moving average defined that way is non-causal (also called non-realizable), because 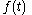depends on future inputs, such as 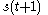. A realizable output is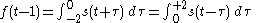which is a delayed version of the non-realizable output.
Any linear filter (such as a moving average) can be characterized by a function h(t) called its impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
. Its output is the convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
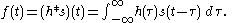
In those terms, causality requires
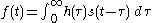
and general equality of these two expressions requires h(t) = 0 for all t < 0.
Characterization of causal filters in the frequency domain
Let h(t) be a causal filter with corresponding Fourier transform H(ω). Define the function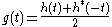which is non-causal. On the other hand, g(t) is Hermitian and, consequently, its Fourier transform G(ω) is real-valued. We now have the following relation
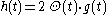
where Θ(t) is the Heaviside unit step function.
This means that the Fourier transforms of h(t) and g(t) are related as follows
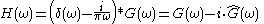
where
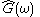is a Hilbert transformHilbert transform
In mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u, and produces a function, H, with the same domain. The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the...
done in the frequency domain (rather than the time domain). The sign of
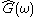may depend on the definition of the Fourier Transform.Taking the Hilbert transform of the above equation yields this relation between "H" and its Hilbert transform: