
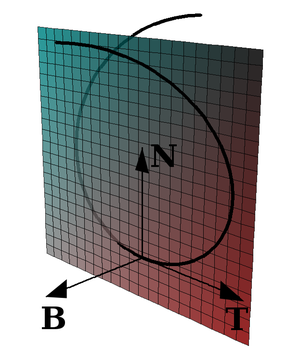
Osculating plane
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly in differential geometry, an osculating plane is a plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
in a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
or affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
which meets a submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
at a point in such a way as to have a second order of contact
Contact (mathematics)
In mathematics, contact of order k of functions is an equivalence relation, corresponding to having the same value at a point P and also the same derivatives there, up to order k. The equivalence classes are generally called jets...
at the point. The word osculate is from the Latin osculatus which is a past participle of osculari, meaning to kiss. An osculating plane is thus a plane which "kisses" a submanifold.
The osculating plane in the geometry of Euclidean space curves can be described in terms of the Frenet-Serret formulas
Frenet-Serret formulas
In vector calculus, the Frenet–Serret formulas describe the kinematic properties of a particle which moves along a continuous, differentiable curve in three-dimensional Euclidean space R3...
as the linear span
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
of the tangent and normal vectors. See also Differential geometry of curves#Special Frenet vectors and generalized curvatures.

