Ostomachion
Encyclopedia

Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
. This work has survived fragmentarily in an Arabic
Arabic language
Arabic is a name applied to the descendants of the Classical Arabic language of the 6th century AD, used most prominently in the Quran, the Islamic Holy Book...
version and in a copy
Archimedes Palimpsest
The Archimedes Palimpsest is a palimpsest on parchment in the form of a codex. It originally was a copy of an otherwise unknown work of the ancient mathematician, physicist, and engineer Archimedes of Syracuse and other authors, which was overwritten with a religious text.Archimedes lived in the...
of the original ancient Greek
Ancient Greek
Ancient Greek is the stage of the Greek language in the periods spanning the times c. 9th–6th centuries BC, , c. 5th–4th centuries BC , and the c. 3rd century BC – 6th century AD of ancient Greece and the ancient world; being predated in the 2nd millennium BC by Mycenaean Greek...
text made in Byzantine
Byzantine Empire
The Byzantine Empire was the Eastern Roman Empire during the periods of Late Antiquity and the Middle Ages, centred on the capital of Constantinople. Known simply as the Roman Empire or Romania to its inhabitants and neighbours, the Empire was the direct continuation of the Ancient Roman State...
times. The word Ostomachion has as its roots in the Greek
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
"Ὀστομάχιον", which means "bone-fight", from "ὀστέον" (osteon), "bone" + "μάχη" (mache), "fight, battle, combat". Note that the manuscripts refer to the word as "Stomachion", an apparent corruption of the original Greek. Ausonius
Ausonius
Decimius Magnus Ausonius was a Latin poet and rhetorician, born at Burdigala .-Biography:Decimius Magnus Ausonius was born in Bordeaux in ca. 310. His father was a noted physician of Greek ancestry and his mother was descended on both sides from long-established aristocratic Gallo-Roman families...
gives us the correct name "Ostomachion" (quod Graeci ostomachion vocavere). The Ostomachion which he describes was a puzzle similar to tangram
Tangram
The tangram is a dissection puzzle consisting of seven flat shapes, called tans, which are put together to form shapes. The objective of the puzzle is to form a specific shape using all seven pieces, which may not overlap...
s and was played perhaps by several persons with pieces made of bone. It is not known which is older, Archimedes' geometrical investigation of the figure, or the game.
Game
The game is a 14-piece dissection puzzle forming a square. One form of play to which classical texts attest is the creation of different objects, animals, plants etc. by rearranging the pieces: an elephant, a tree, a barking dog, a ship, a sword, a tower etc. Another suggestion is that it exercised and developed memory skills in the young. James Gow, in his Short History of Greek Mathematics (1884), footnotes that the purpose was to put the pieces back in their box, and this was also a view expressed by W. W. Rouse Ball in some intermediate editions of Mathematical Essays and Recreations, but edited out from 1939.Mathematical problem
In the fragment in Arabic translated by Heinrich Suter it is shown that each of the pieces has an area that is a rational fraction of the total area of the dissected parallelogram. In the Greek version of the treatise, some investigation is made as to the sizes of the angles of the pieces to see which could go together to make a straight line. This might have been preparatory to consideration of the number of ways the pieces might reform some prescribed shape, for example the box in which the pieces were contained, although there is not enough of the Greek text remaining to be sure. If this is the case, then Archimedes anticipated aspects of combinatoricsCombinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
. Combinatorics often involves finding the number of ways a given problem can be solved, subject to well-defined constraints. For example, the number of ways of reforming a square using the pieces as proposed by Suter is 536 without distinguishing the result up to rotations
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
and reflections
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
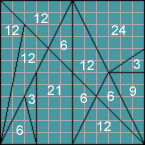
of the square, but allowing the pieces to be turned over. One such solution is shown in colour to the right. However, if pieces are not allowed to be turned over, for example, if obverse and reverse can be distinguished or, in the case of Suter's pieces, on account of the sharpness of some angles, the corresponding number is 4. If rotations and reflections are treated as distinct, these numbers rise to 17,152 and 64, respectively. The counts of 4 and 64 may be verified easily as lower bounds by elementary group theory, but were confirmed as exact by Bill Cutler shortly after his determination of the count 536 and by the same computer program. So, there are at least four different answers that we might give just considering Suter's proposal. Clearly, to count, you have to know what counts. When, as here, the number of outcomes is so sensitive to the assumptions made, it helps to state them explicitly. Put another way, combinatorics can help sharpen our awareness of tacit assumptions. If, say, answers like 4 or 64 are unacceptable for some reason, we have to re-examine our presumptions, possibly questioning whether Suter's pieces can be turned over in reforming their square. As emerges below, there is also some objection to Suter's proposal which would render this combinatorial discussion of the Suter board academic.
The Greek text of the fragment can also be found in the Bibliotheca Augustana website.
This is an English translation, with added disambiguation in brackets, of the text of the fragmentary Arabic manuscript (translated from Heinrich Suter's German translation in: Archimedis opera omnia, vol. 2, p. 420 sqq., ed. J. L. Heiberg, Leipzig 1881, as published in the Bibliotheca Augustana website):
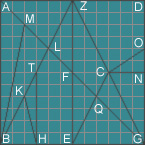
" We draw a [rectangular] parallelogram ABGD, we bisect BG in E and draw EZ perpendicular to BG [to intersect AD], we draw the diagonals AG, BZ [intersecting AG at L], and ZG, we also bisect BE in H, and draw HT perpendicular to BE [to intersect BZ], then we put the ruler at point H and - looking to point A - we draw HK [to intersect BZ], then bisect AL in M, and draw BM. So the A-E rectangle is divided into seven parts.
Now we bisect DG in N, ZG in C, we draw EC and attaching the ruler to the points B and C we draw CO [to intersect DG], furthermore CN. Thus the rectangle ZG is also divided in seven parts, but in another way than the first one. Therefore, the whole square has fourteen parts.
We now demonstrate that each of the fourteen parts is in rational relationship to the whole square.
Because ZG is the diagonal of the rectangle Z-G, the triangle DZG is half of this rectangle, that means 1/4 of the square. But the triangle GNC is 1/4 of triangle DZG, because, if we extend the line EC, it comes to point D, and that means triangle GDC has half area of the triangle DZG and is equal to the two triangles GNC and DNC taken together; that means triangle GNC is 1/16 of the square. If we presume that line OC is orientated to point B, as we have drawn it before, so the line NC is parallel to BG, which is the side of the square and of the triangle OBG, so we get the proportion
BG : NC = GO : NO.
But BG is four times NC, and in the same way GO four times NO; therefore is GN three times NO, and triangle GNC = 3 ONC. However, as we have shown, triangle GNC is 1/16 of the square, that means triangle ONC = 1/48 of the square. Furthermore, as triangle GDZ = 1/4 of the square, and therefore GNC = 1/16 of that triangle and NCO = 1/48 of that, it remains for the quadrilateral DOCZ = 1/6 of the square’s area. According to the proposition that line NC [extended] intersects [ZE at] point F, and GE is parallel to CF, [and labelling the intersection of AG and CE as Q,] we get the proportion
EC : CF = EQ : CQ = GQ : FQ.
Because EQ = 2 CQ and GQ = 2 FQ, triangle EQG is double to the two triangles GCQ and EFQ. It is clear, that triangle EGZ = 2 times triangle EFG, because ZE = 2 FE. As the triangle EGZ = 1/4 of the square, that means triangle EFG = 1/8 of the square. This triangle is three times as big as each of the two triangles EFQ and GCQ, so each of these two triangles = 1/24 of the square A-G. And the triangle EGQ is double to each of the two triangles EFQ and GCQ, so it is = 1/12 of the square. Furthermore because ZF = EF, triangle ZFG = triangle EFG. If we now take away triangle GCQ (= triangle EFQ), it leaves quadrilateral FQCZ (= triangle EGQ), therefore quadrilateral FQCZ = 1/12 of the square A-G.
We have now divided the rectangle Z-G in 7 parts, and go on to divide the other rectangle.
Because BZ and EC are two parallel diagonals, and ZF = EF, therefore triangle ZLF = EFQ, and also triangle ZLF = 1/24 of the square A-G. Because BH = HE, triangle BEZ is four times the triangle BHT, because each of them is rectangular. As triangle BEZ = 1/4 of the square ABGD, triangle BHT = 1/16 of that. According to our proposition the line HK [extended[ intersects point A, so we get the proportion
AB : HT = BK : KT.
Because AB = 2 HT, and BK = 2 KT and BT = 3 KT, triangle BHT is three times the triangle KHT. However, because triangle BHT = 1/16 of the whole square, triangle KHT = 1/48 of that. Triangle BKH is double the triangle KHT, so = 1/24 of the square. Further, as BL = 2 ZL, and AL = 2 LF, triangle ABL is twice the triangle ALZ, and ALZ double the triangle ZLF. However, because triangle ZLF = 1/24 of the whole square, triangle ALZ = 1/12 of that, so triangle ABL = 1/6. But triangle ABM = triangle BML, so each of these two triangles = 1/12 of the square. It leaves the pentagon LFEHT = 7/48 of the entire square.
We have now also divided the square AE into 7 sections, therefore, the whole figure ABGD in 14 parts. Each of these fourteen parts is in rational relationship to the whole, and that is what we wanted."
However, Suter was translating unpointed Arabic, in which, as he concedes, equals and twice are easily confused. At a crucial
point in his translation he ignores this in making his figure a square; instead he makes a typographical error, equating, not
the sides, but a side and a diagonal, in which case the figure cannot be a rectangle. Suter does know that, for the areal
results discussed in the text, it suffices that the figure be a parallelogram. Suter may have been under the impression that
the figure had to be a square, so made it one.
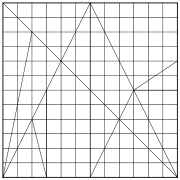
The dissection lines given by Archimedes' Stomachion from the Archimedes Codex
Archimedes Palimpsest
The Archimedes Palimpsest is a palimpsest on parchment in the form of a codex. It originally was a copy of an otherwise unknown work of the ancient mathematician, physicist, and engineer Archimedes of Syracuse and other authors, which was overwritten with a religious text.Archimedes lived in the...
, as agreed by Heiberg and Dijksterhuis, are a subset of those of Suter's square board when the latter is subjected to a lateral stretch by a factor of two. This was recognised by Richard Dixon Oldham
Richard Dixon Oldham
Richard Dixon Oldham FRS was a British geologist who made the first clear identification of the separate arrivals of P-waves, S-waves and surface waves on seismograms and the first clear evidence that the Earth has a central core.-Life:Born on 31 July 1858 to Thomas Oldham, a Fellow of the Royal...
, FRS, in a letter to Nature in March, 1926. The letter triggered a wave of interest in the dissection puzzle, with kits for sale and a feature article in The New York Times that August; Popular Science Monthly had related items in its issues for November, 1926 and February, March, May and June, 1927, including Stomachion competitions with cash prizes. As each of the two unit squares is cut diagonally, the pieces can be arranged in a single square of side the square root of two, after the manner deployed by Socrates
Socrates
Socrates was a classical Greek Athenian philosopher. Credited as one of the founders of Western philosophy, he is an enigmatic figure known chiefly through the accounts of later classical writers, especially the writings of his students Plato and Xenophon, and the plays of his contemporary ...
in Plato's Meno. Thus, the 14 pieces still form a square, even when the dissected board is not a square. Naturally, the count of solutions also changes, but here we now have three possible boxes: the two unit squares side by side; the two unit squares one on top of the other; and this single square of side the square root of two. The single square can be formed from four congruent right isosceles triangles, but this can also be accomplished with three right isosceles triangles, two congruent and the third double their area, as in Tangram
Tangram
The tangram is a dissection puzzle consisting of seven flat shapes, called tans, which are put together to form shapes. The objective of the puzzle is to form a specific shape using all seven pieces, which may not overlap...
, as well as in a third way where only one right isosceles triangle is formed. (Bill Cutler has made a comprehensive study of the associated counts comparable to those mentioned for the Suter board.) With two exceptions, the pieces can be formed from right triangles with legs in the ratios 1:1, 1:2 and 1:3, with some pieces similar to others, possibly at different scales; this observation provides a comparatively easy means to determine the proportional areas of the pieces.
Suter's translation can now be checked against the fragment of Archimedes' Stomachion in the Archimedes Codex
Archimedes Palimpsest
The Archimedes Palimpsest is a palimpsest on parchment in the form of a codex. It originally was a copy of an otherwise unknown work of the ancient mathematician, physicist, and engineer Archimedes of Syracuse and other authors, which was overwritten with a religious text.Archimedes lived in the...
, as was presumably not open to Suter himself when he made the translation. Heiberg, followed by Dijksterhius, seem to have thought that the two texts, the Greek discussing angles, the Arabic areas, were so different there was no relation between the two, so may have felt there was nothing to check. But, in Suter's square, the diagonals cross at right angles, whence the nature the angles examined in the first proposition of Archimedes' Stomachion, whether acute or obtuse, is immediate, making it puzzling why Archimedes would prove this as a proposition. Instead, the first proposition, if it is seen to relate to the underlying figure of the dissected Stomachion board, sets up two squares side by side, in which setting the nature of the angles is more sensitive, but still tractable. The two squares separately suggest two frames of an iterative process. If this process is continued, rational approximations of the square root of two are obtained; these are the side-diameter numbers familiar to the Greeks. At each step of the process, the nature of the angles switches back and forth, highlighting the significance of the first proposition. Whether or not this has any bearing on Archimedes' Stomachion is another matter, but it does provide a geometrical means to handle recurrence relations if you do not have algebraic notation, such as subscripts, and the geometry is fully within Archimedes' capabilities. The same technique readily produces the bounds for the square root of three that Archimedes assumes without comment in Measurement of a Circle
Measurement of a Circle
Measurement of a Circle is a treatise that consists of three propositions by Archimedes. The treatise is only a fraction of what was a longer work.-Proposition one:Proposition one states:...
; if it were applied to the dissection of a square proposed by Suter, analogous bounds for the square root of five are obtained. The geometry can be worked independently of knowledge of Pell's equation
Pell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
or of the properties of convergents of a continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
, but to similar effect.
The dissection of the two squares side by side can also be seen as a layered composite or collage of instances of the diagrams for Elements II.9, 10. Viewed numerically, these propositions provide the link between the legs of right triangles in the unit square grid and those of right triangles in the overlaid diagonal square grid where the right triangles share their hypotenuse, although Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
proves them in terms of geometrical lines. Thus, pairs of successive side numbers in the overlaid grid are associated with pairs of successive diameter numbers in the unit square grid, as remarked by Proclus
Proclus
Proclus Lycaeus , called "The Successor" or "Diadochos" , was a Greek Neoplatonist philosopher, one of the last major Classical philosophers . He set forth one of the most elaborate and fully developed systems of Neoplatonism...
, rather than side and diameter numbers being paired. The ratios within these pairs are then rational approximations for the tangent of π/8, in agreement with the iterative process of the previous paragraph, which is, in effect, an angle bisection algorithm. This reminds us that a natural setting for the side-diameter numbers is a nest of regular octagons. The analogue for the square root of three is not an angle bisection algorithm, but it does produce rational approximations to the tangent of π/12, with the regular dodecagon as a setting. Instead of simply approximating the square roots in each case, we can approximate the corresponding regular polygons. But, again, whether this was actually Archimedes' agenda is another matter.
Irrespective of the parallelogram adopted for the Stomachion board, the presence of several centroids of triangles on the board as further points of it might seem another Archimedean theme, not least as they facilitate the computation of the relative areas of the pieces. Most obviously, Q is the centroid of the right triangle GZE, so the pieces in that triangle are either one sixth or one third of it. But similarly K is the centroid of right triangle EAB, so triangle HKB has area one sixth of it. In Equilibrium of Planes, Archimedes makes use of the concurrence of the three medians of a triangle in the centroid, but does not prove it. As it happens, for both K and Q, we see two medians intersecting in them, but the pairings are not the same, although the triangles GZE and EAB are translations of one another.
Selected bibliography
- J. L. Heiberg, Archimedis opera omnia, vol. 2, S. 420 ff., Leipzig: Teubner 1881
- Reviel Netz & William Noel, The Archimedes Codex (Weidenfeld & Nicholson, 2007)
- J. Väterlein, Roma ludens (Heuremata - Studien zu Literatur, Sprachen und Kultur der Antike, Bd. 5), Amsterdam: Verlag B. R. Grüner bv 1976
External links
- Heinrich Suter, Loculus
- James Gow, Short History
- W. W. R. Ball, Recreations and Essays
- Ostomachion, a Graeco-Roman puzzle
- Professor Chris Rorres
- Kolata, Gina. "In Archimedes' Puzzle, a New Eureka Moment." The New York Times. December 14, 2003
- A tour of Archimedes' Stomachion, by Fan ChungFan ChungFan Rong K Chung Graham , known professionally as Fan Chung, is a mathematician who works mainly in the areas of spectral graph theory, extremal graph theory and random graphs, in particular...
and Ronald GrahamRonald GrahamRonald Lewis Graham is a mathematician credited by the American Mathematical Society as being "one of the principal architects of the rapid development worldwide of discrete mathematics in recent years"...
.