
Parallel (curve)
Encyclopedia
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
is the envelope
Envelope (mathematics)
In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...
of a family of congruent circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s centered on the curve. It generalises the concept of parallel lines
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
. It can also be defined as a curve whose points are at a fixed normal distance of a given curve.
It is sometimes called the offset curve but the term "offset" often refers also to translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
. The term "offset curve" is used, e.g., in numerically controlled machining
Machining
Conventional machining is a form of subtractive manufacturing, in which a collection of material-working processes utilizing power-driven machine tools, such as saws, lathes, milling machines, and drill presses, are used with a sharp cutting tool to physical remove material to achieve a desired...
(and in other computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
applications), where it describes the shape of the cut made by a round cutting piece, which is "offset" from the trajectory of the cutter by a constant distance in the direction normal to the cutter trajectory at every point.
A curve that is a parallel of itself is autoparallel. The involute
Involute
In the differential geometry of curves, an involute is a curve obtained from another given curve by attaching an imaginary taut string to the given curve and tracing its free end as it is wound onto that given curve; or in reverse, unwound. It is a roulette wherein the rolling curve is a straight...
of a circle is an example.
Alternative definitions
Alternatively, one can fix a circle and a point on the curve and take the envelope of the translations taking that point to the circle.Tracing the center of a circle rolled along the curve (see roulette
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, and involutes....
) would give one branch of a parallel.
Parametric curve
For a parametrically defined curve, the following equations define one branch of its parallel curve with distance (the other branch is obtained with
(the other branch is obtained with  ):
):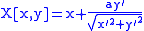
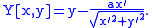
Geometric properties
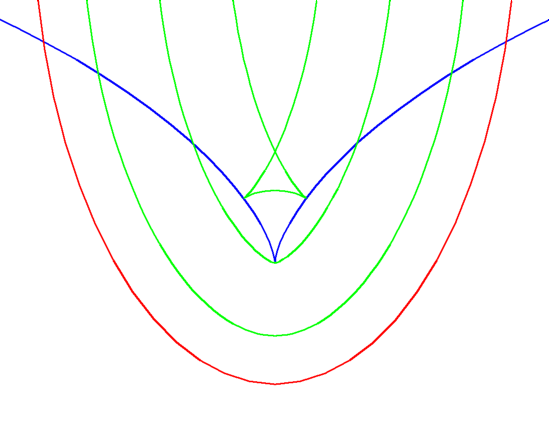
As for parallel lines, a normal line to a curve is also normal to its parallels.When parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
curves are constructed they will have cusps when the distance from the curve matches the radius of curvature. These are the points where the curve touches the evolute
Evolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. Equivalently, it is the envelope of the normals to a curve....
.
If the initial curve is a boundary of a planar set and its parallel curve is without self-intersections, then the latter is the boundary of the Minkowski sum of the planar set and the disk of the given radius.

