
Parity anomaly
Encyclopedia
In theoretical physics
a quantum field theory
is said to have a parity anomaly if its classical action
is invariant under a change of parity
of the universe, but the quantum theory is not invariant.
This kind of anomaly
can occur in odd-dimensional gauge theories with fermions whose gauge groups have odd dual Coxeter numbers. They were first introduced by Antti J. Niemi and Gordon Walter Semenoff
in the letter Axial-Anomaly-Induced Fermion Fractionization and Effective Gauge-Theory Actions in Odd-Dimensional Space-Times and by A. Norman Redlich in the letter Gauge Noninvariance and Parity Nonconservation of Three-Dimensional Fermions and the article Parity violation and gauge noninvariance of the effective gauge field action in three dimensions. It is in some sense an odd-dimensional version of Edward Witten
's SU(2) anomaly in 4-dimensions, and in fact Redlich writes that his demonstration follows Witten's.
s which transform under a real representation
of G. This theory naively suffers from an ultraviolet divergence
. If one includes a gauge-invariant regulator
then the quantum parity invariance of the theory will be broken if h and n are odd.
 is not parity invariant, therefore the possibility exists that the parity invariance may remain when the mass goes to infinity. Indeed, this is the source of the anomaly.
is not parity invariant, therefore the possibility exists that the parity invariance may remain when the mass goes to infinity. Indeed, this is the source of the anomaly.
If n is even, then one may rewrite the n Majorana fermions as n/2 Dirac fermion
s. These have parity invariant mass terms, and so Pauli–Villars may be used to regulate the divergences and no parity anomaly arises. Therefore for even n there is no anomaly. Moreover, as the contribution of 2n Majorana fermions to the partition function
is the square of the contribution of n fermions, the square of the contribution to the anomaly of n fermions must be equal to one. Therefore the anomalous phase may only be equal to a square root of one, in other words, plus or minus one. If it is equal to one, then there is no anomaly. Therefore the question is, when is there an ambiguity in the partition function of a factor of -1.
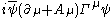
where Ψ is a Majorana fermion and A is the vector potential
. In the path integral
, the exponential of the action is integrated over all of the fields. When integrating the above term over the fermion fields one obtains a factor of the square root
of the determinant
of the Dirac operator
for each of the n Majorana fermions.
As is usual with a square root, one needs to determine its sign. The overall phase of the partition function is not an observable
in quantum mechanics, and so for a given configuration this sign choice can be made arbitrarily. But one needs to check that the sign choice is consistent. To do this, let us deform the configuration through the configuration space
, on a path which eventually returns to the original configuration. If the sign choice was consistent then, having returned to the original configuration, one will have the original sign. This is what needs to be checked.
The original spacetime is 3-dimensional, call the space M. Now we are considering a circle in configuration space, which is the same thing as a single configuration on the space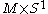 . To find out the number of times that the sign of the square root vanishes as one goes around the circle, it suffices to count the number of zeroes of the determinant on
. To find out the number of times that the sign of the square root vanishes as one goes around the circle, it suffices to count the number of zeroes of the determinant on 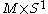 , because each time that a pair of eigenvalues changes sign there will be a zero. Notice that the eigenvalues come in pairs, as discussed for example in Supersymmetric Index Of Three-Dimensional Gauge Theory, and so whenever one eigenvalue crosses zero, two will cross.
, because each time that a pair of eigenvalues changes sign there will be a zero. Notice that the eigenvalues come in pairs, as discussed for example in Supersymmetric Index Of Three-Dimensional Gauge Theory, and so whenever one eigenvalue crosses zero, two will cross.
Summarizing, we want to know how many times the sign of the square root of the determinant of a Dirac operator changes sign as one circumnavigates
the circle. The eigenvalues of the Dirac operator come in pairs, and the sign changes each time a pair crosses zero. Thus we are counting the zeroes of the Dirac operator on the space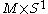 . These zeroes are counted by the Atiyah-Singer index theorem, which gives the answer h times the second Chern class
. These zeroes are counted by the Atiyah-Singer index theorem, which gives the answer h times the second Chern class
of the gauge bundle over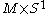 . This second Chern class may be any integer. In particular it may be one, in which case the sign changes h times. If the sign changes an odd number of times then the partition function is ill-defined, and so there is an anomaly.
. This second Chern class may be any integer. In particular it may be one, in which case the sign changes h times. If the sign changes an odd number of times then the partition function is ill-defined, and so there is an anomaly.
In conclusion, we have found that there is an anomaly if the number n of Majorana fermions is odd and if the dual Coxeter number h of the gauge group is also odd.
are also anomalous when their level is half-integral. In fact, the derivation is identical to that above. Using Stokes' theorem
and the fact that the exterior derivative of the Chern-Simons action
is equal to the instanton
number, the 4-dimensional theory on has a theta angle equal to the level of the Chern-Simons theory, and so the 4-dimensional partition function is equal to -1 precisely when the instanton number is odd. This implies that the 3-dimensional partition function is ill-defined by a factor of -1 when considering deformations over a path with an odd number of instantons.
has a theta angle equal to the level of the Chern-Simons theory, and so the 4-dimensional partition function is equal to -1 precisely when the instanton number is odd. This implies that the 3-dimensional partition function is ill-defined by a factor of -1 when considering deformations over a path with an odd number of instantons.
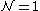 supersymmetric Chern-Simons gauge theories presented in The Chern-Simons Coefficient in Supersymmetric Yang-Mills Chern-Simons Theories. When n=2 this contribution to the partition function was found in
supersymmetric Chern-Simons gauge theories presented in The Chern-Simons Coefficient in Supersymmetric Yang-Mills Chern-Simons Theories. When n=2 this contribution to the partition function was found in 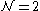 and 3 gauge theories in Branes and Supersymmetry Breaking in Three Dimensional Gauge Theories.
and 3 gauge theories in Branes and Supersymmetry Breaking in Three Dimensional Gauge Theories.
the Chern–Simons level of the corresponding gauge theory by −n/2. The fact that the Chern–Simons level is only allowed to take discrete values implies that the coupling constant
can not enter into the correction to the level. This only occurs for the 1-loop correction, therefore the contribution of the Majorana fermions to the Chern–Simons level may be precisely calculated at 1-loop and all higher loop corrections vanish.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
a quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
is said to have a parity anomaly if its classical action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
is invariant under a change of parity
Parity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
of the universe, but the quantum theory is not invariant.
This kind of anomaly
Anomaly (physics)
In quantum physics an anomaly or quantum anomaly is the failure of a symmetry of a theory's classical action to be a symmetry of any regularization of the full quantum theory. In classical physics an anomaly is the failure of a symmetry to be restored in the limit in which the symmetry-breaking...
can occur in odd-dimensional gauge theories with fermions whose gauge groups have odd dual Coxeter numbers. They were first introduced by Antti J. Niemi and Gordon Walter Semenoff
Gordon Walter Semenoff
Gordon Walter Semenoff is a theoretical physicist and Professor of Physics at University of British Columbia. He is known for his research on quantum mechanics, quantum field theory, statistical mechanics and string theory and is particularly famous for his co-invention, together with Antti Niemi,...
in the letter Axial-Anomaly-Induced Fermion Fractionization and Effective Gauge-Theory Actions in Odd-Dimensional Space-Times and by A. Norman Redlich in the letter Gauge Noninvariance and Parity Nonconservation of Three-Dimensional Fermions and the article Parity violation and gauge noninvariance of the effective gauge field action in three dimensions. It is in some sense an odd-dimensional version of Edward Witten
Edward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
's SU(2) anomaly in 4-dimensions, and in fact Redlich writes that his demonstration follows Witten's.
The anomaly in 3-dimensions
Consider a classically parity-invariant gauge theory whose gauge group G has dual coxeter number h in 3-dimensions. Include n Majorana fermionMajorana fermion
In physics, a Majorana fermion is a fermion which is its own anti-particle. The term is used in opposition to Dirac fermion, which describes particles that differ from their antiparticles...
s which transform under a real representation
Real representation
In the mathematical field of representation theory a real representation is usually a representation on a real vector space U, but it can also mean a representation on a complex vector space V with an invariant real structure, i.e., an antilinear equivariant mapj\colon V\to V\,which...
of G. This theory naively suffers from an ultraviolet divergence
Ultraviolet divergence
In physics, an ultraviolet divergence is a situation in which an integral, for example a Feynman diagram, diverges because of contributions of objects with very high energy , or, equivalently, because of physical phenomena at very short distances. An infinite answer to a question that should have a...
. If one includes a gauge-invariant regulator
Regularization (physics)
-Introduction:In physics, especially quantum field theory, regularization is a method of dealing with infinite, divergent, and non-sensical expressions by introducing an auxiliary concept of a regulator...
then the quantum parity invariance of the theory will be broken if h and n are odd.
The anomaly can only be a choice of sign
Consider for example Pauli–Villars regularization. One needs to add n massive Majorana fermions with opposite statistics and take their masses to infinity. The complication arises from the fact that the 3-dimensional Majorana mass term, is not parity invariant, therefore the possibility exists that the parity invariance may remain when the mass goes to infinity. Indeed, this is the source of the anomaly.
is not parity invariant, therefore the possibility exists that the parity invariance may remain when the mass goes to infinity. Indeed, this is the source of the anomaly.If n is even, then one may rewrite the n Majorana fermions as n/2 Dirac fermion
Dirac fermion
In particle physics, a Dirac fermion is a fermion which is not its own anti-particle. It is named for Paul Dirac. All fermions in the standard model, except possibly neutrinos, are Dirac fermions...
s. These have parity invariant mass terms, and so Pauli–Villars may be used to regulate the divergences and no parity anomaly arises. Therefore for even n there is no anomaly. Moreover, as the contribution of 2n Majorana fermions to the partition function
Partition function (quantum field theory)
In quantum field theory, we have a generating functional, Z[J] of correlation functions and this value, called the partition function is usually expressed by something like the following functional integral:...
is the square of the contribution of n fermions, the square of the contribution to the anomaly of n fermions must be equal to one. Therefore the anomalous phase may only be equal to a square root of one, in other words, plus or minus one. If it is equal to one, then there is no anomaly. Therefore the question is, when is there an ambiguity in the partition function of a factor of -1.
Anomaly from the index theorem
We want to know when the choice of sign of the partition function is ill-defined. The possibility that it be ill-defined exists because the action contains the fermion kinetic term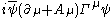
where Ψ is a Majorana fermion and A is the vector potential
Vector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
. In the path integral
Path integral
Path integral may refer to:* Line integral, the integral of a function along a curve* Functional integration, the integral of a functional over a space of curves...
, the exponential of the action is integrated over all of the fields. When integrating the above term over the fermion fields one obtains a factor of the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the Dirac operator
Dirac operator
In mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian...
for each of the n Majorana fermions.
As is usual with a square root, one needs to determine its sign. The overall phase of the partition function is not an observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
in quantum mechanics, and so for a given configuration this sign choice can be made arbitrarily. But one needs to check that the sign choice is consistent. To do this, let us deform the configuration through the configuration space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
, on a path which eventually returns to the original configuration. If the sign choice was consistent then, having returned to the original configuration, one will have the original sign. This is what needs to be checked.
The original spacetime is 3-dimensional, call the space M. Now we are considering a circle in configuration space, which is the same thing as a single configuration on the space
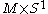 . To find out the number of times that the sign of the square root vanishes as one goes around the circle, it suffices to count the number of zeroes of the determinant on
. To find out the number of times that the sign of the square root vanishes as one goes around the circle, it suffices to count the number of zeroes of the determinant on 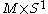 , because each time that a pair of eigenvalues changes sign there will be a zero. Notice that the eigenvalues come in pairs, as discussed for example in Supersymmetric Index Of Three-Dimensional Gauge Theory, and so whenever one eigenvalue crosses zero, two will cross.
, because each time that a pair of eigenvalues changes sign there will be a zero. Notice that the eigenvalues come in pairs, as discussed for example in Supersymmetric Index Of Three-Dimensional Gauge Theory, and so whenever one eigenvalue crosses zero, two will cross.Summarizing, we want to know how many times the sign of the square root of the determinant of a Dirac operator changes sign as one circumnavigates
Circumnavigation
Circumnavigation – literally, "navigation of a circumference" – refers to travelling all the way around an island, a continent, or the entire planet Earth.- Global circumnavigation :...
the circle. The eigenvalues of the Dirac operator come in pairs, and the sign changes each time a pair crosses zero. Thus we are counting the zeroes of the Dirac operator on the space
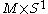 . These zeroes are counted by the Atiyah-Singer index theorem, which gives the answer h times the second Chern class
. These zeroes are counted by the Atiyah-Singer index theorem, which gives the answer h times the second Chern classChern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
of the gauge bundle over
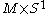 . This second Chern class may be any integer. In particular it may be one, in which case the sign changes h times. If the sign changes an odd number of times then the partition function is ill-defined, and so there is an anomaly.
. This second Chern class may be any integer. In particular it may be one, in which case the sign changes h times. If the sign changes an odd number of times then the partition function is ill-defined, and so there is an anomaly.In conclusion, we have found that there is an anomaly if the number n of Majorana fermions is odd and if the dual Coxeter number h of the gauge group is also odd.
Chern–Simons gauge theories
3-dimensional Chern-Simons gauge theoriesChern-Simons theory
The Chern–Simons theory is a 3-dimensional topological quantum field theory of Schwarz type, introduced by Edward Witten. It is so named because its action is proportional to the integral of the Chern–Simons 3-form....
are also anomalous when their level is half-integral. In fact, the derivation is identical to that above. Using Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
and the fact that the exterior derivative of the Chern-Simons action
Chern-Simons form
In mathematics, the Chern–Simons forms are certain secondary characteristic classes. They have been found to be of interest in gauge theory, and they define the action of Chern–Simons theory...
is equal to the instanton
Instanton
An instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory...
number, the 4-dimensional theory on
 has a theta angle equal to the level of the Chern-Simons theory, and so the 4-dimensional partition function is equal to -1 precisely when the instanton number is odd. This implies that the 3-dimensional partition function is ill-defined by a factor of -1 when considering deformations over a path with an odd number of instantons.
has a theta angle equal to the level of the Chern-Simons theory, and so the 4-dimensional partition function is equal to -1 precisely when the instanton number is odd. This implies that the 3-dimensional partition function is ill-defined by a factor of -1 when considering deformations over a path with an odd number of instantons.Fractional quantization conditions
In particular, the anomalies coming from fermions and the half-level Chern-Simons terms will cancel if and only if the number of Majorana fermions plus twice the Chern–Simons level is even. In the case n=1, this statement is the half-integer quantization condition in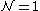 supersymmetric Chern-Simons gauge theories presented in The Chern-Simons Coefficient in Supersymmetric Yang-Mills Chern-Simons Theories. When n=2 this contribution to the partition function was found in
supersymmetric Chern-Simons gauge theories presented in The Chern-Simons Coefficient in Supersymmetric Yang-Mills Chern-Simons Theories. When n=2 this contribution to the partition function was found in 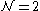 and 3 gauge theories in Branes and Supersymmetry Breaking in Three Dimensional Gauge Theories.
and 3 gauge theories in Branes and Supersymmetry Breaking in Three Dimensional Gauge Theories.One-loop correction to the Chern–Simons level
The fact that both Chern–Simons terms and Majorana fermions are anomalous under deformations with odd instanton numbers is not a coincidence. When the Pauli–Villars mass for n Majorana fermions is taken to infinity, Redlich found that the remaining contribution to the partition function is equal to a Chern-Simons term at level −n/2. This means in particular that integrating out n charged Majorana fermions renormalizesRenormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
the Chern–Simons level of the corresponding gauge theory by −n/2. The fact that the Chern–Simons level is only allowed to take discrete values implies that the coupling constant
Coupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
can not enter into the correction to the level. This only occurs for the 1-loop correction, therefore the contribution of the Majorana fermions to the Chern–Simons level may be precisely calculated at 1-loop and all higher loop corrections vanish.

