Paul Leyland
Encyclopedia
Paul Leyland is a British
number theorist
who has studied integer factorization
and primality test
ing.
He has contributed to the factorization of RSA-129, RSA-140, and RSA-155, as well as potential factorial prime
s as large as 400! + 1. He has also studied Cunningham number
s, Cullen number
s, Woodall number
s, etc., and numbers of the form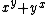
, which are now called Leyland number
s. He was involved with the NFSNet project to use distributed computing
on the Internet
from 2005 to 2008.
In 2002 he co-authored a paper with Samuel S. Wagstaff Jr.
entitled "MPQS with three large primes" in the Proceedings of the Algorithmic Number Theory Symposium 2002. Since Wagstaff co-authored a paper with Paul Erdős
, this means Leyland has an Erdős number
of 2.
United Kingdom
The United Kingdom of Great Britain and Northern IrelandIn the United Kingdom and Dependencies, other languages have been officially recognised as legitimate autochthonous languages under the European Charter for Regional or Minority Languages...
number theorist
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
who has studied integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
and primality test
Primality test
A primality test is an algorithm for determining whether an input number is prime. Amongst other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not...
ing.
He has contributed to the factorization of RSA-129, RSA-140, and RSA-155, as well as potential factorial prime
Factorial prime
A factorial prime is a prime number that is one less or one more than a factorial . The first few factorial primes are:n! − 1 is prime for :n! + 1 is prime for :...
s as large as 400! + 1. He has also studied Cunningham number
Cunningham number
In mathematics, specifically in number theory, a Cunningham number is a certain kind of integer named after English mathematician A. J. C. Cunningham.-Definition:Cunningham numbers are a simple type of binomial number, they are of the formb^n\pm1\,...
s, Cullen number
Cullen number
In mathematics, a Cullen number is a natural number of the form n · 2n + 1 . Cullen numbers were first studied by Fr. James Cullen in 1905...
s, Woodall number
Woodall number
In number theory, a Woodall number is any natural number of the formfor some natural number n. The first few Woodall numbers are:Woodall numbers were first studied by Allan J. C. Cunningham and H. J. Woodall in 1917, inspired by James Cullen's earlier study of the similarly-defined Cullen numbers...
s, etc., and numbers of the form
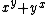, which are now called Leyland numberLeyland number
In number theory, a Leyland number is a number of the form xy + yx, where x and y are integers greater than 1. The first few Leyland numbers are...
s. He was involved with the NFSNet project to use distributed computing
Distributed computing
Distributed computing is a field of computer science that studies distributed systems. A distributed system consists of multiple autonomous computers that communicate through a computer network. The computers interact with each other in order to achieve a common goal...
on the Internet
Internet
The Internet is a global system of interconnected computer networks that use the standard Internet protocol suite to serve billions of users worldwide...
from 2005 to 2008.
In 2002 he co-authored a paper with Samuel S. Wagstaff Jr.
Samuel S. Wagstaff Jr.
Samuel Standfield Wagstaff, Jr. is an American mathematician and computer scientist whose research interests are in the areas of cryptography, parallel computation, and analysis of algorithms, especially number theoretic algorithms...
entitled "MPQS with three large primes" in the Proceedings of the Algorithmic Number Theory Symposium 2002. Since Wagstaff co-authored a paper with Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
, this means Leyland has an Erdős number
Erdos number
The Erdős number describes the "collaborative distance" between a person and mathematician Paul Erdős, as measured by authorship of mathematical papers.The same principle has been proposed for other eminent persons in other fields.- Overview :...
of 2.