Woodall number
Encyclopedia
In number theory
, a Woodall number (Wn) is any natural number
of the form
for some natural number n. The first few Woodall numbers are:
Woodall numbers were first studied by Allan J. C. Cunningham and H. J. Woodall
in 1917, inspired by James Cullen
's earlier study of the similarly-defined Cullen number
s. Woodall numbers curiously arise in Goodstein's theorem
.
Woodall numbers that are also prime number
s are called Woodall primes; the first few exponents n for which the corresponding Woodall numbers Wn are prime are 2, 3, 6, 30, 75, 81, 115, 123, 249, 362, 384, … ; the Woodall primes themselves begin with 7, 23, 383, 32212254719, … .
In 1976 Christopher Hooley
showed that almost all
Cullen numbers are composite
. Hooley's proof was reworked by Hiromi Suyama to show that it works for any sequence of numbers n · 2n+a + b where a and b are integers, and in particular also for Woodall numbers. Nonetheless, it is conjectured that there are infinitely many Woodall primes. , the largest known Woodall prime is 3752948 × 23752948 − 1. It has 1,129,757 digits and was found by Matthew J. Thompson in 2007 in the distributed computing
project PrimeGrid
.
Like Cullen numbers, Woodall numbers have many divisibility properties. For example, if p is a prime number, then p divides
A generalized Woodall number is defined to be a number of the form n × bn − 1, where n + 2 > b; if a prime can be written in this form, it is then called a generalized Woodall prime.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a Woodall number (Wn) is any natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
of the form
- Wn = n × 2n − 1
for some natural number n. The first few Woodall numbers are:
- 1, 7, 23, 63, 159, 383, 895, … .
Woodall numbers were first studied by Allan J. C. Cunningham and H. J. Woodall
H. J. Woodall
Herbert J. Woodall was a British mathematician.In 1925 Lt.-Col. Allan J.C. Cunningham and Woodall gathered together all that was known about the primality and factorization of such numbers and published a small book of tables...
in 1917, inspired by James Cullen
James Cullen (mathematician)
Father James Cullen, S.J. was born at Drogheda, County Louth, Ireland.He studied mathematics at the Trinity College, Dublin for a while, but eventually turned to theology and was ordained as a Jesuit on 1 July 1901....
's earlier study of the similarly-defined Cullen number
Cullen number
In mathematics, a Cullen number is a natural number of the form n · 2n + 1 . Cullen numbers were first studied by Fr. James Cullen in 1905...
s. Woodall numbers curiously arise in Goodstein's theorem
Goodstein's theorem
In mathematical logic, Goodstein's theorem is a statement about the natural numbers, made by Reuben Goodstein, which states that every Goodstein sequence eventually terminates at 0. showed that it is unprovable in Peano arithmetic...
.
Woodall numbers that are also prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s are called Woodall primes; the first few exponents n for which the corresponding Woodall numbers Wn are prime are 2, 3, 6, 30, 75, 81, 115, 123, 249, 362, 384, … ; the Woodall primes themselves begin with 7, 23, 383, 32212254719, … .
In 1976 Christopher Hooley
Christopher Hooley
Christopher Hooley FLSW FRS is a British mathematician, emeritus professor of mathematics at Cardiff University. He did his PhD under the supervision of Albert Ingham. He won the Adams Prize of Cambridge University in 1973. He was elected a Fellow of the Royal Society in 1983...
showed that almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
Cullen numbers are composite
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
. Hooley's proof was reworked by Hiromi Suyama to show that it works for any sequence of numbers n · 2n+a + b where a and b are integers, and in particular also for Woodall numbers. Nonetheless, it is conjectured that there are infinitely many Woodall primes. , the largest known Woodall prime is 3752948 × 23752948 − 1. It has 1,129,757 digits and was found by Matthew J. Thompson in 2007 in the distributed computing
Distributed computing
Distributed computing is a field of computer science that studies distributed systems. A distributed system consists of multiple autonomous computers that communicate through a computer network. The computers interact with each other in order to achieve a common goal...
project PrimeGrid
PrimeGrid
PrimeGrid is a distributed computing project for searching for prime numbers of world-record size. It makes use of the Berkeley Open Infrastructure for Network Computing platform...
.
Like Cullen numbers, Woodall numbers have many divisibility properties. For example, if p is a prime number, then p divides
- W(p + 1) / 2 if the Jacobi symbolJacobi symbolThe Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in...
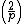is +1 and
- W(3p − 1) / 2 if the Jacobi symbol
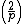is −1.
A generalized Woodall number is defined to be a number of the form n × bn − 1, where n + 2 > b; if a prime can be written in this form, it is then called a generalized Woodall prime.
External links
- Chris Caldwell, The Prime Glossary: Woodall number at The Prime PagesPrime pagesThe Prime Pages is a website about prime numbers maintained by Chris Caldwell at the University of Tennessee at Martin.The site maintains the list of the "5,000 largest known primes", selected smaller primes of special forms, and many "top twenty" lists for primes of various forms...
. - Steven Harvey, List of Generalized Woodall primes.
- Paul Leyland, Generalized Cullen and Woodall Numbers