Perfectly matched layer
Encyclopedia
A perfectly matched layer (PML) is an artificial absorbing layer for wave equation
s, commonly used to truncate computational regions in numerical methods to simulate problems with open boundaries, especially in the FDTD and FEM
methods. The key property of a PML that distinguishes it from an ordinary absorbing material is that it is designed so that waves incident upon the PML from a non-PML medium do not reflect at the interface—this property allows the PML to strongly absorb outgoing waves from the interior of a computational region without reflecting them back into the interior.
PML was originally formulated by Berenger in 1994 for use with Maxwell's equations
, and since that time there have been several related reformulations of PML for both Maxwell's equations and for other wave equations. Berenger's original formulation is called a split-field PML, because it splits the electromagnetic field
s into two unphysical fields in the PML region. A later formulation that has become more popular because of its simplicity and efficiency is called uniaxial PML or UPML (Gedney, 1996), in which the PML is described as an artificial anisotropic
absorbing material. Although both Berenger's formulation and UPML were initially derived by manually constructing the conditions under which incident plane wave
s do not reflect from the PML interface from a homogeneous medium, both formulations were later shown to be equivalent to a much more elegant and general approach: stretched-coordinate PML (Chew and Weedon, 1994; Teixeira and Chew, 1998). In particular, PMLs were shown to correspond to a coordinate transformation in which one (or more) coordinates are mapped to complex number
s; more technically, this is actually an analytic continuation
of the wave equation into complex coordinates, replacing propagating (oscillating) waves by exponentially decaying waves. This viewpoint allows PMLs to be derived for inhomogeneous media such as waveguide
s, as well as for other coordinate system
s and wave equations.
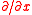appears in the wave equation, it is replaced by:
where ω is the angular frequency
and σ is some function
of x. Wherever σ is positive, propagating waves are attenuated because: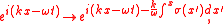
where we have taken a planewave propagating in the +x direction (for
) and applied the transformation (analytic continuation) to complex coordinates: 
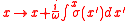, or equivalently 
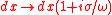. The same coordinate transformation causes waves to attenuate whenever their x dependence is in the form 
for some propagation constant
k: this includes planewaves propagating at some angle with the x axis and also transverse mode
s of a waveguide.
The above coordinate transformation can be left as-is in the transformed wave equations, or can be combined with the material description (e.g. the permittivity
and permeability
in Maxwell's equations) to form a UPML description. Note also that the coefficient σ/ω depends upon frequency—this is so the attenuation rate is proportional to k/ω, which is independent of frequency in a homogeneous material (not including material dispersion, e.g. for vacuum
) because of the dispersion relation
between ω and k. However, this frequency-dependence means that a time domain
implementation of PML, e.g. in the FDTD method, is more complicated than for a frequency-independent absorber, and involves the auxiliary differential equation (ADE) approach (equivalently, i/ω appears as an integral
or convolution
in time domain).
Perfectly matched layers, in their original form, only attenuate propagating waves; purely evanescent waves (exponentially decaying fields) oscillate in the PML but do not decay more quickly. However, the attenuation of evanescent waves can also be accelerated by including a real
coordinate stretching in the PML: this corresponds to making σ in the above expression a complex number
, where the imaginary part yields a real coordinate stretching that causes evanescent waves to decay more quickly.
One caveat with perfectly matched layers is that they are only reflectionless for the exact wave equation. Once the wave equation is discretized
for simulation on a computer, some small numerical reflections appear. For this reason, the PML absorption coefficient σ is typically turned on gradually from zero (e.g. quadratically
) over a short distance on the scale of the wavelength
of the wave.
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
s, commonly used to truncate computational regions in numerical methods to simulate problems with open boundaries, especially in the FDTD and FEM
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
methods. The key property of a PML that distinguishes it from an ordinary absorbing material is that it is designed so that waves incident upon the PML from a non-PML medium do not reflect at the interface—this property allows the PML to strongly absorb outgoing waves from the interior of a computational region without reflecting them back into the interior.
PML was originally formulated by Berenger in 1994 for use with Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, and since that time there have been several related reformulations of PML for both Maxwell's equations and for other wave equations. Berenger's original formulation is called a split-field PML, because it splits the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
s into two unphysical fields in the PML region. A later formulation that has become more popular because of its simplicity and efficiency is called uniaxial PML or UPML (Gedney, 1996), in which the PML is described as an artificial anisotropic
Birefringence
Birefringence, or double refraction, is the decomposition of a ray of light into two rays when it passes through certain anisotropic materials, such as crystals of calcite or boron nitride. The effect was first described by the Danish scientist Rasmus Bartholin in 1669, who saw it in calcite...
absorbing material. Although both Berenger's formulation and UPML were initially derived by manually constructing the conditions under which incident plane wave
Plane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
s do not reflect from the PML interface from a homogeneous medium, both formulations were later shown to be equivalent to a much more elegant and general approach: stretched-coordinate PML (Chew and Weedon, 1994; Teixeira and Chew, 1998). In particular, PMLs were shown to correspond to a coordinate transformation in which one (or more) coordinates are mapped to complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s; more technically, this is actually an analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
of the wave equation into complex coordinates, replacing propagating (oscillating) waves by exponentially decaying waves. This viewpoint allows PMLs to be derived for inhomogeneous media such as waveguide
Waveguide
A waveguide is a structure which guides waves, such as electromagnetic waves or sound waves. There are different types of waveguides for each type of wave...
s, as well as for other coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
s and wave equations.
Technical description
Specifically, for a PML designed to absorb waves propagating in the x direction, the following transformation is included in the wave equation. Wherever an x derivative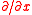 appears in the wave equation, it is replaced by:where ω is the angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
and σ is some function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of x. Wherever σ is positive, propagating waves are attenuated because:
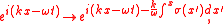
where we have taken a planewave propagating in the +x direction (for
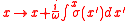) and applied the transformation (analytic continuation) to complex coordinates: , or equivalently 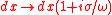. The same coordinate transformation causes waves to attenuate whenever their x dependence is in the form for some propagation constantPropagation constant
The propagation constant of an electromagnetic wave is a measure of the change undergone by the amplitude of the wave as it propagates in a given direction. The quantity being measured can be the voltage or current in a circuit or a field vector such as electric field strength or flux density...
k: this includes planewaves propagating at some angle with the x axis and also transverse mode
Transverse mode
A transverse mode of a beam of electromagnetic radiation is a particular electromagnetic field pattern of radiation measured in a plane perpendicular to the propagation direction of the beam...
s of a waveguide.
The above coordinate transformation can be left as-is in the transformed wave equations, or can be combined with the material description (e.g. the permittivity
Permittivity
In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
and permeability
Permeability (electromagnetism)
In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it is the degree of magnetization that a material obtains in response to an applied magnetic field. Magnetic permeability is typically...
in Maxwell's equations) to form a UPML description. Note also that the coefficient σ/ω depends upon frequency—this is so the attenuation rate is proportional to k/ω, which is independent of frequency in a homogeneous material (not including material dispersion, e.g. for vacuum
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
) because of the dispersion relation
Dispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
between ω and k. However, this frequency-dependence means that a time domain
Time domain
Time domain is a term used to describe the analysis of mathematical functions, physical signals or time series of economic or environmental data, with respect to time. In the time domain, the signal or function's value is known for all real numbers, for the case of continuous time, or at various...
implementation of PML, e.g. in the FDTD method, is more complicated than for a frequency-independent absorber, and involves the auxiliary differential equation (ADE) approach (equivalently, i/ω appears as an integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
or convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
in time domain).
Perfectly matched layers, in their original form, only attenuate propagating waves; purely evanescent waves (exponentially decaying fields) oscillate in the PML but do not decay more quickly. However, the attenuation of evanescent waves can also be accelerated by including a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
coordinate stretching in the PML: this corresponds to making σ in the above expression a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, where the imaginary part yields a real coordinate stretching that causes evanescent waves to decay more quickly.
One caveat with perfectly matched layers is that they are only reflectionless for the exact wave equation. Once the wave equation is discretized
Discretization
In mathematics, discretization concerns the process of transferring continuous models and equations into discrete counterparts. This process is usually carried out as a first step toward making them suitable for numerical evaluation and implementation on digital computers...
for simulation on a computer, some small numerical reflections appear. For this reason, the PML absorption coefficient σ is typically turned on gradually from zero (e.g. quadratically
Quadratic function
A quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....
) over a short distance on the scale of the wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
of the wave.