
Phonon scattering
Encyclopedia
Phonons can scatter through several mechanisms as they travel through the material. These scattering mechanisms are: Umklapp phonon-phonon scattering
, phonon-impurity scattering, phonon-electron scattering, and phonon-boundary scattering. Each scattering mechanism can be characterised by relaxation rate 1/ which is reverse to relaxation time.
which is reverse to relaxation time.
All scattering processes can be taken into account using Matthiessen's rule. Then the combined relaxation time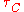 can be written as:
can be written as:

The parameters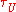 ,
,  ,
, 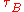 ,
, 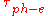 are due to Umklapp scattering, mass-difference impurity scattering, boundary scattering and phonon-electron scattering, respectively.
are due to Umklapp scattering, mass-difference impurity scattering, boundary scattering and phonon-electron scattering, respectively.
 and umklapp processes vary with
and umklapp processes vary with 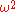 , Umklapp scattering dominates at high frequency.
, Umklapp scattering dominates at high frequency.  is given by:
is given by:
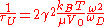
where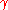 is Gruneisen anharmonicity parameter
is Gruneisen anharmonicity parameter
, μ is shear modulus, V0 is volume per atom and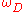 is Debye frequency
is Debye frequency
.
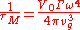
where is a measure of the impurity scattering strength. Note that
is a measure of the impurity scattering strength. Note that  is dependent of the dispersion curves.
is dependent of the dispersion curves.
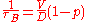
where D is the dimension of the system and p represents the surface roughness parameter. The value p=1 means a smooth perfect surface that the scattering is purely specular and the relaxation time goes to ∞; hence, boundary scattering does not affect thermal transport. The value p=0 represents a very rough surface that the scattering is then purely diffusive which gives:
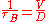
This equation is also known as Casimir limit.

The parameter is conduction electrons concentration, ε is deformation potential, ρ is mass density and m* is effective electron mass. It is usually assumed that contribution to thermal conductivity by phonon-electron scattering is negligible.
is conduction electrons concentration, ε is deformation potential, ρ is mass density and m* is effective electron mass. It is usually assumed that contribution to thermal conductivity by phonon-electron scattering is negligible.
Umklapp scattering
Umklapp scattering is the transformation, like a reflection or a translation, of a wave vector to another Brillouin zone as a result of a scattering process, for example an electron-lattice potential scattering or an anharmonic phonon-phonon scattering process, reflecting an electronic state or...
, phonon-impurity scattering, phonon-electron scattering, and phonon-boundary scattering. Each scattering mechanism can be characterised by relaxation rate 1/
 which is reverse to relaxation time.
which is reverse to relaxation time.All scattering processes can be taken into account using Matthiessen's rule. Then the combined relaxation time
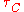 can be written as:
can be written as:
The parameters
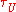 ,
,  ,
, 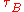 ,
, 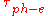 are due to Umklapp scattering, mass-difference impurity scattering, boundary scattering and phonon-electron scattering, respectively.
are due to Umklapp scattering, mass-difference impurity scattering, boundary scattering and phonon-electron scattering, respectively.Phonon-phonon scattering
For phonon-phonon scattering, effects by normal processes (processes which conserve the phonon wave vector - N processes) are ignored in favor of Umklapp processes (U processes). Since normal processes vary linearly with and umklapp processes vary with
and umklapp processes vary with 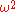 , Umklapp scattering dominates at high frequency.
, Umklapp scattering dominates at high frequency.  is given by:
is given by: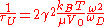
where
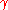 is Gruneisen anharmonicity parameter
is Gruneisen anharmonicity parameterGrüneisen Parameter
The Grüneisen parameter, γ, named after Eduard Grüneisen, describes the effect that changing the volume of a crystal lattice has on its vibrational properties, and, as a consequence, the effect that changing temperature has on the size or dynamics of the lattice...
, μ is shear modulus, V0 is volume per atom and
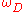 is Debye frequency
is Debye frequencyDebye frequency
The Debye frequency of a crystal is a theoretical maximum frequency of vibration for the atoms that make up the crystal . It was proposed by Peter Debye as part of the Debye model. It is generally not the same as the actual maximum oscillation frequency for the crystal, due to approximations in the...
.
Mass-difference impurity scattering
Mass-difference impurity scattering is given by: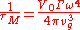
where
 is a measure of the impurity scattering strength. Note that
is a measure of the impurity scattering strength. Note that  is dependent of the dispersion curves.
is dependent of the dispersion curves.Boundary scattering
Boundary scattering is particularly important for low-dimensional nanostructures and its relaxation time is given by: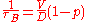
where D is the dimension of the system and p represents the surface roughness parameter. The value p=1 means a smooth perfect surface that the scattering is purely specular and the relaxation time goes to ∞; hence, boundary scattering does not affect thermal transport. The value p=0 represents a very rough surface that the scattering is then purely diffusive which gives:
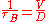
This equation is also known as Casimir limit.
Phonon-electron scattering
Phonon-electron scattering can also contribute when the material is lightly doped. The corresponding relaxation time is given as:
The parameter
 is conduction electrons concentration, ε is deformation potential, ρ is mass density and m* is effective electron mass. It is usually assumed that contribution to thermal conductivity by phonon-electron scattering is negligible.
is conduction electrons concentration, ε is deformation potential, ρ is mass density and m* is effective electron mass. It is usually assumed that contribution to thermal conductivity by phonon-electron scattering is negligible.

