Physical geodesy is the study of the physical properties of the gravity field of the Earth, the geopotential

Geopotential

Geopotential is the potential of the Earth's gravity field. For convenience it is often defined as minus the potential energy per unit mass, so that the gravity vector is obtained as the gradient of this potential, without the minus....

, with a view to their application in geodesy

Geodesy

Geodesy , also named geodetics, a branch of earth sciences, is the scientific discipline that deals with the measurement and representation of the Earth, including its gravitational field, in a three-dimensional time-varying space. Geodesists also study geodynamical phenomena such as crustal...

.

Measurement procedure

Traditional geodetic instruments such as theodolite

Theodolite

A theodolite is a precision instrument for measuring angles in the horizontal and vertical planes. Theodolites are mainly used for surveying applications, and have been adapted for specialized purposes in fields like metrology and rocket launch technology...

s rely on the gravity field for orienting their vertical axis along the local plumb line or local vertical direction

Vertical direction

In astronomy, geography, geometry and related sciences and contexts, a direction passing by a given point is said to be vertical if it is locally aligned with the gradient of the gravity field, i.e., with the direction of the gravitational force at that point...

 with the aid of a spirit level

Spirit level

A spirit level or bubble level is an instrument designed to indicate whether a surface ishorizontal or vertical . Different types of spirit levels may be used by carpenters, stonemasons, bricklayers, other building trades workers, surveyors, millwrights and other metalworkers, and in some...

. After that, vertical angle

Angle

In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...

s (zenith

Zenith

The zenith is an imaginary point directly "above" a particular location, on the imaginary celestial sphere. "Above" means in the vertical direction opposite to the apparent gravitational force at that location. The opposite direction, i.e...

 angles or, alternatively, elevation

Elevation

The elevation of a geographic location is its height above a fixed reference point, most commonly a reference geoid, a mathematical model of the Earth's sea level as an equipotential gravitational surface ....

 angles) are obtained with respect to this local vertical, and horizontal angles in the plane of the local horizon, perpendicular to the vertical.

Levelling

Levelling

Levelling or leveling is a branch of surveying, the object of which is1) To find the elevation of a given point with respect to the given or assumed Datum.2) to establish a point at a given elevation with respect to the given or assumed Datum....

 instruments again are used to obtain geopotential

Geopotential

Geopotential is the potential of the Earth's gravity field. For convenience it is often defined as minus the potential energy per unit mass, so that the gravity vector is obtained as the gradient of this potential, without the minus....

 differences between points on the Earth's surface. These can then be expressed as "height" differences by conversion to metric units.

The geopotential

The Earth's gravity field can be described by a potential

Potential

*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...

 as follows:


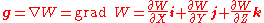
which expresses the gravitational acceleration vector as the gradient of , the potential of gravity. The vector triad 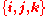is the orthonormal set of base vectors in space, pointing along the 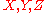coordinate axes.

Note that both gravity and its potential contain a contribution from the centrifugal pseudo-force

Centrifugal force

Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...

 due to the Earth's rotation. We can write


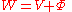
where is the potential of the gravitational field, that of the gravity field, and 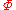that of the centrifugal force field.

The centrifugal force is given by


where


is the vector pointing to the point considered straight from the Earth's rotational axis.
It can be shown that this pseudo-force field, in a reference frame co-rotating with the Earth, has a potential associated with it that looks like this:


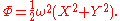
This can be verified by taking the gradient () operator of this expression.

Here, , and are geocentric coordinates

Geocentric coordinates

Geocentric coordinates are an Earth-centered system of locating objects in the solar system in three-dimensions along the Cartesian X, Y and Z axes. They are differentiated from topocentric coordinates which use the observer's location as the reference point for bearings in altitude and azimuth...

.

Units of gravity and geopotential

Gravity is commonly measured in units of m·s⁻², (metre

Metre

The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology...

s per second

Second

The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....

 squared). This also can be expressed (multiplying by the gravitational constant

Gravitational constant

The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...

 G in order to change units) as newtons per kilogram

Kilogram

The kilogram or kilogramme , also known as the kilo, is the base unit of mass in the International System of Units and is defined as being equal to the mass of the International Prototype Kilogram , which is almost exactly equal to the mass of one liter of water...

 of attracted mass.

Potential is expressed as gravity times distance, m²·s⁻². Travelling one metre in the direction of a gravity vector of strength 1 m·s⁻² will increase your potential by 1 m²·s⁻². Again employing G as a multipier, the units can be changed to joule

Joule

The joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...

s per kilogram of attracted mass.

A more convenient unit is the GPU, or geopotential unit: it equals 10 m²·s⁻². This means that travelling one metre in the vertical direction, i.e., the direction of the 9.8 m·s⁻² ambient gravity, will approximately change your potential by 1 GPU. Which again means that the difference in geopotential, in GPU, of a point with that of sea level can be used as a rough measure of height "above sea level" in metres.

The normal potential

To a rough approximation, the Earth is a sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

, or to a much better approximation, an ellipsoid. We can similarly approximate the gravity field of the Earth by a spherically symmetric field:


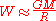
of which the equipotential surfaces—the surfaces of constant potential value—are concentric spheres.

It is more accurate to approximate the geopotential by a field that has the Earth reference ellipsoid as one of its equipotential surfaces, however. The most recent Earth reference ellipsoid is GRS80, or Geodetic Reference System 1980, which the Global Positioning system uses as its reference. Its geometric parameters are: semi-major axis a = 6378137.0 m, and flattening f = 1/298.257222101.

A geopotential field is constructed, being the sum of a gravitational potential and the known centrifugal potential 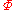, that has the GRS80 reference ellipsoid as one of its equipotential surfaces. If we also require that the enclosed mass is equal to the known mass of the Earth (including atmosphere) GM = 3986005 × 10⁸ m³·s⁻², we obtain for the potential at the reference ellipsoid: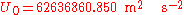


Obviously, this value depends on the assumption that the potential goes asymptotically to zero at infinity (), as is common in physics. For practical purposes it makes more sense to choose the zero point of normal gravity to be that of the reference ellipsoid

Reference ellipsoid

In geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....

, and refer the potentials of other points to this.

Disturbing potential and geoid

Once a clean, smooth geopotential field has been constructed matching the known GRS80 reference ellipsoid with an equipotential surface (we call such a field a normal potential) we can subtract it from the true (measured) potential of the real Earth. The result is defined as T, the disturbing potential:


The disturbing potential T is numerically a great deal smaller than U or W, and captures the detailed, complex variations of the true gravity field of the actually existing Earth from point-to-point, as distinguished from the overall global trend captured by the smooth mathematical ellipsoid of the normal potential.

Due to the irregularity of the Earth's true gravity field, the equilibrium figure of sea water, or the geoid

Geoid

The geoid is that equipotential surface which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest , and extended through the continents . According to C.F...

, will also be of irregular form. In some places, like west of Ireland

Ireland

Ireland is an island to the northwest of continental Europe. It is the third-largest island in Europe and the twentieth-largest island on Earth...

, the geoid—mathematical mean sea level—sticks out as much as 100 m above the regular, rotationally symmetric reference ellipsoid of GRS80; in other places, like close to Ceylon, it dives under the ellipsoid by nearly the same amount. The separation between these two surfaces is called the undulation of the geoid

Undulation of the geoid

Undulation of the geoid is the mathematical process of determining the height in meters above the geoid from the height provided by the GPS system which uses the ellipsoid as reference...

, symbol , and is closely related to the disturbing potential.

According to the famous Bruns formula, we have


where 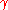is the force of gravity computed from the normal field potential .

In 1849, the mathematician George Gabriel Stokes

George Gabriel Stokes

Sir George Gabriel Stokes, 1st Baronet FRS , was an Irish mathematician and physicist, who at Cambridge made important contributions to fluid dynamics , optics, and mathematical physics...

 published the following formula named after him:


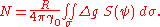
In this formula, 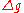stands for gravity anomalies, differences between true and normal (reference) gravity, and S is the Stokes function, a kernel function derived by Stokes in closed analytical form. (Note that determining anywhere on Earth by this formula requires 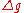to be known everywhere on Earth. Welcome to the role of international co-operation in physical geodesy.)

The geoid

Geoid

The geoid is that equipotential surface which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest , and extended through the continents . According to C.F...

, or mathematical mean sea surface, is defined not only on the seas, but also under land; it is the equilibrium water surface that would result, would sea water be allowed to move freely (e.g., through tunnels) under the land. Technically, an equipotential surface of the true geopotential, chosen to coincide (on average) with mean sea level.

As mean sea level is physically realized by tide gauge bench marks on the coasts of different countries and continents, a number of slightly incompatible "near-geoids" will result, with differences of several decimetres to over one metre between them, due to the dynamic sea surface topography. These are referred to as vertical or height datums.

For every point on Earth, the local direction of gravity or vertical direction

Vertical direction

In astronomy, geography, geometry and related sciences and contexts, a direction passing by a given point is said to be vertical if it is locally aligned with the gradient of the gravity field, i.e., with the direction of the gravitational force at that point...

, materialized with the plumb line, is perpendicular to the geoid. On this is based a method, astrogeodetic levelling, for deriving the local figure of the geoid by measuring deflections of the vertical

Vertical deflection

The vertical deflection at a point on the earth is a measure of how far the direction of the local gravity field has been shifted by local anomalies such as nearby mountains....

by astronomical means over an area.

Gravity anomalies

Above we already made use of gravity anomalies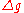 . These are computed as the differences between true (observed) gravity , and calculated (normal) gravity . (This is an oversimplification; in practice the location in space at which γ is evaluated will differ slightly from that where g has been measured.) We thus get


These anomalies are called free-air anomalies

Free-air anomaly

In geophysics, the free-air gravity anomaly, often simply called the free-air anomaly, is the measured gravity anomaly after a free-air correction is applied to correct for the elevation at which a measurement is made...

, and are the ones to be used in the above Stokes equation.

In geophysics

Geophysics

Geophysics is the physics of the Earth and its environment in space; also the study of the Earth using quantitative physical methods. The term geophysics sometimes refers only to the geological applications: Earth's shape; its gravitational and magnetic fields; its internal structure and...

, these anomalies are often further reduced by removing from them the attraction of the topography, which for a flat, horizontal plate (Bouguer plate) of thickness H is given by


The Bouguer reduction to be applied as follows:


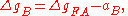
so-called Bouguer anomalies

Bouguer anomaly

In geodesy and geophysics, the Bouguer anomaly is a gravity anomaly, corrected for the height at which it is measured and the attraction of terrain. The height correction alone gives a free-air anomaly.-Bouguer reduction:...

. Here, 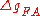is our earlier 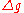, the free-air anomaly.

In case the terrain is not a flat plate (the usual case!) we use for H the local terrain height value but apply a further correction called the terrain correction (TC).