Poincaré–Hopf theorem
Encyclopedia
In mathematics
, the Poincaré–Hopf theorem (also known as the Poincaré–Hopf index formula, Poincaré–Hopf index theorem, or Hopf index theorem) is an important theorem that is still used today in differential topology
. It is named after Henri Poincaré
and Heinz Hopf
.
The Poincaré–Hopf theorem is often
illustrated by the special case of the Hairy ball theorem
, which simply states that there is no smooth vector field on a sphere having no sources or sinks.
orientable differentiable manifold
. Let v be a vector field
on M with isolated zeroes. If M has boundary
, then we insist that v be pointing in the outward normal direction along the boundary. Then we have the formula
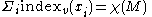
where the sum of the indices is over all the isolated zeroes of v and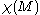
is the Euler characteristic
of M.
The theorem was proven for two dimensions by Henri Poincaré
and later generalized to higher dimensions by Heinz Hopf
.
concept, whereas the index of a vector field is purely analytic. Thus, this theorem establishes a deep link between two seemingly unrelated areas of mathematics. It is perhaps as interesting that the proof of this theorem relies heavily on integral
, and, in particular, Stokes' theorem
, which states that the integral of the exterior derivative
of a differential form
is equal to the integral of that form over the boundary. In the special case of a manifold without boundary, this amounts to saying that the integral is 0. But by examining vector fields in a sufficiently small neighborhood of a source or sink, we see that sources and sinks contribute integral
amounts (known as the index) to the total, and they must all sum to 0. This result may be considered one of the earliest of a whole series of theorems establishing deep relationships between geometric
and analytical or physical
concepts. They play an important role in the modern study of both fields.
2. Take a small neighborhood of M in that Euclidean space, Nε. Extend the vector field to this neighborhood so that it still has the same zeroes and the zeroes have the same indices. In addition, make sure that the extended vector field at the boundary of Nε is directed outwards.
3. The sum of indices of the zeroes of the old (and new) vector field is equal to the degree of the Gauss map
from the boundary of Nε to the sphere. Thus, the sum of the indices is independent of the actual vector field, and depends only on the manifold M.
Technique: cut away all zeroes of the vector field with small neighborhoods. Then use the fact that the degree of a map from the boundary of an n-dimensional manifold to an sphere, that can be extended to the whole n-dimensional manifold, is zero.
4. Finally, identify this sum of indices as the Euler characteristic of M. To do that, construct a very specific vector field on M using a triangulation
of M for which it is clear that the sum of indices is equal to the Euler characteristic.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Poincaré–Hopf theorem (also known as the Poincaré–Hopf index formula, Poincaré–Hopf index theorem, or Hopf index theorem) is an important theorem that is still used today in differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
. It is named after Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
and Heinz Hopf
Heinz Hopf
Heinz Hopf was a German mathematician born in Gräbschen, Germany . He attended Dr. Karl Mittelhaus' higher boys' school from 1901 to 1904, and then entered the König-Wilhelm- Gymnasium in Breslau. He showed mathematical talent from an early age...
.
The Poincaré–Hopf theorem is often
illustrated by the special case of the Hairy ball theorem
Hairy ball theorem
The hairy ball theorem of algebraic topology states that there is no nonvanishing continuous tangent vector field on an even-dimensional n-sphere. An ordinary sphere is a 2-sphere, so that this theorem will hold for an ordinary sphere...
, which simply states that there is no smooth vector field on a sphere having no sources or sinks.
Formal statement
Theorem. Let M be a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
orientable differentiable manifold
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
. Let v be a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
on M with isolated zeroes. If M has boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
, then we insist that v be pointing in the outward normal direction along the boundary. Then we have the formula
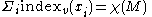
where the sum of the indices is over all the isolated zeroes of v and
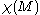is the Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of M.
The theorem was proven for two dimensions by Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
and later generalized to higher dimensions by Heinz Hopf
Heinz Hopf
Heinz Hopf was a German mathematician born in Gräbschen, Germany . He attended Dr. Karl Mittelhaus' higher boys' school from 1901 to 1904, and then entered the König-Wilhelm- Gymnasium in Breslau. He showed mathematical talent from an early age...
.
Significance
The Euler characteristic of a closed surface is a purely topologicalTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
concept, whereas the index of a vector field is purely analytic. Thus, this theorem establishes a deep link between two seemingly unrelated areas of mathematics. It is perhaps as interesting that the proof of this theorem relies heavily on integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
, and, in particular, Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
, which states that the integral of the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
of a differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
is equal to the integral of that form over the boundary. In the special case of a manifold without boundary, this amounts to saying that the integral is 0. But by examining vector fields in a sufficiently small neighborhood of a source or sink, we see that sources and sinks contribute integral
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
amounts (known as the index) to the total, and they must all sum to 0. This result may be considered one of the earliest of a whole series of theorems establishing deep relationships between geometric
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and analytical or physical
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
concepts. They play an important role in the modern study of both fields.
Sketch of proof
1. Embed M in some high-dimensional Euclidean space. (Use the Whitney embedding theorem.)2. Take a small neighborhood of M in that Euclidean space, Nε. Extend the vector field to this neighborhood so that it still has the same zeroes and the zeroes have the same indices. In addition, make sure that the extended vector field at the boundary of Nε is directed outwards.
3. The sum of indices of the zeroes of the old (and new) vector field is equal to the degree of the Gauss map
Gauss map
In differential geometry, the Gauss map maps a surface in Euclidean space R3 to the unit sphere S2. Namely, given a surface X lying in R3, the Gauss map is a continuous map N: X → S2 such that N is a unit vector orthogonal to X at p, namely the normal vector to X at p.The Gauss map can be defined...
from the boundary of Nε to the sphere. Thus, the sum of the indices is independent of the actual vector field, and depends only on the manifold M.
Technique: cut away all zeroes of the vector field with small neighborhoods. Then use the fact that the degree of a map from the boundary of an n-dimensional manifold to an sphere, that can be extended to the whole n-dimensional manifold, is zero.
4. Finally, identify this sum of indices as the Euler characteristic of M. To do that, construct a very specific vector field on M using a triangulation
Triangulation (topology)
In mathematics, topology generalizes the notion of triangulation in a natural way as follows:A triangulation of a topological space X is a simplicial complex K, homeomorphic to X, together with a homeomorphism h:K\to X....
of M for which it is clear that the sum of indices is equal to the Euler characteristic.