Poisson's equation
Encyclopedia
In mathematics
, Poisson's equation is a partial differential equation
of elliptic type with broad utility in electrostatics
, mechanical engineering
and theoretical physics
. It is named after the French
mathematician
, geometer and physicist
Siméon-Denis Poisson.
The Poisson equation is
where
is the Laplace operator
, and f and φ are real
or complex
-valued functions
on a manifold
. When the manifold is Euclidean space
, the Laplace operator is often denoted as
and so Poisson's equation is frequently written as
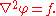
In three-dimensional Cartesian coordinates, it takes the form
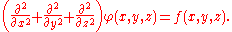
For vanishing f, this equation becomes Laplace's equation
The Poisson equation may be solved using a Green's function
; a general exposition of the Green's function for the Poisson equation is given in the article on the screened Poisson equation
. There are various methods for numerical solution. The relaxation method
, an iterative algorithm, is one example.
is the posing and solving of problems that are described by the Poisson equation. Finding φ for some given f is an important practical problem, since this is the usual way to find the electric potential
for a given charge
distribution.
The derivation of Poisson's equation in electrostatics follows. SI
units are used and Euclidean space is assumed.
Starting with Gauss' law for electricity (also part of Maxwell's equations
) in a differential control volume, we have:
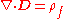
Assuming the medium is linear, isotropic, and homogeneous (see polarization density
), then:
By substitution and division, we have:
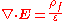
In the absence of a changing magnetic field,
, Faraday's law of induction
gives:
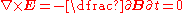
Since the curl of the electric field is zero, it is defined by a scalar electric potential field,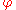
(see Helmholtz decomposition
).
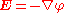
Eliminating
by substitution, we have a form of the Poisson equation:
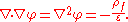
Solving Poisson's equation for the potential requires knowing the charge density distribution. If the charge density is zero, then Laplace's equation
results. If the charge density follows a Boltzmann distribution
, then the Poisson-Boltzmann equation
results. The Poisson–Boltzmann equation plays a role in the development of the Debye–Hückel theory of dilute electrolyte solutions.
(Note: Although the above discussion assumes that the magnetic field is not varying in time, the same Poisson equation arises even if it does vary in time, as long as the Coulomb gauge is used. However, in this more general context, computing
is no longer sufficient to calculate 
, since the latter also depends on the magnetic vector potential, which must be independently computed.)
:
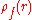where Q is the total charge,
then the solution φ (r) of Poisson's equation,
,
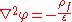is given by
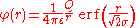
where erf(x) is the error function
.
This solution can be checked explicitly by evaluating
.
Note that, for r much greater than σ, the erf function approaches unity and the potential φ (r) approaches the point charge potential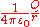
, as one would expect. Furthermore the erf function approaches 1 extremely quickly as its argument increases; in practice for r > 3σ the relative error is smaller than one part in a thousand.
with a mass density 
:
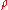Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Poisson's equation is a partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
of elliptic type with broad utility in electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
, mechanical engineering
Mechanical engineering
Mechanical engineering is a discipline of engineering that applies the principles of physics and materials science for analysis, design, manufacturing, and maintenance of mechanical systems. It is the branch of engineering that involves the production and usage of heat and mechanical power for the...
and theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
. It is named after the French
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, geometer and physicist
Physicist
A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
Siméon-Denis Poisson.
The Poisson equation is
where
is the Laplace operatorLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
, and f and φ are real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
on a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
. When the manifold is Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, the Laplace operator is often denoted as
and so Poisson's equation is frequently written as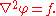In three-dimensional Cartesian coordinates, it takes the form
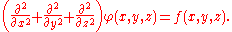
For vanishing f, this equation becomes Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
The Poisson equation may be solved using a Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
; a general exposition of the Green's function for the Poisson equation is given in the article on the screened Poisson equation
Screened Poisson equation
In Physics, the screened Poisson equation is the following partial differential equation:\left[ \Delta - \lambda^2 \right] u = - f...
. There are various methods for numerical solution. The relaxation method
Relaxation method
In numerical mathematics, relaxation methods are iterative methods for solving systems of equations, including nonlinear systems.Relaxation methods were developed for solving large sparse linear systems, which arose as finite-difference discretizations of differential equations...
, an iterative algorithm, is one example.
Electrostatics
One of the cornerstones of electrostaticsElectrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
is the posing and solving of problems that are described by the Poisson equation. Finding φ for some given f is an important practical problem, since this is the usual way to find the electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
for a given charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
distribution.
The derivation of Poisson's equation in electrostatics follows. SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units are used and Euclidean space is assumed.
Starting with Gauss' law for electricity (also part of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
) in a differential control volume, we have:
-
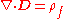
is the divergence operatorDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
.
is the electric displacement field.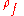
is the free charge densityCharge densityThe linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as...
(describing charges brought from outside).
Assuming the medium is linear, isotropic, and homogeneous (see polarization density
Polarization density
In classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is...
), then:
-
is the permittivityPermittivityIn electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
of the medium.
is the electric fieldElectric fieldIn physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
.
By substitution and division, we have:
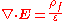
In the absence of a changing magnetic field,
, Faraday's law of inductionFaraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
gives:
-
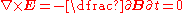
is the curl operator.
is time.
Since the curl of the electric field is zero, it is defined by a scalar electric potential field,
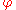(see Helmholtz decompositionHelmholtz decomposition
In physics and mathematics, in the area of vector calculus, Helmholtz's theorem, also known as the fundamental theorem of vector calculus, states that any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational vector field and a...
).
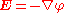
Eliminating
by substitution, we have a form of the Poisson equation: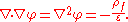Solving Poisson's equation for the potential requires knowing the charge density distribution. If the charge density is zero, then Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
results. If the charge density follows a Boltzmann distribution
Boltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
, then the Poisson-Boltzmann equation
Poisson-Boltzmann equation
The Poisson–Boltzmann equation is a differential equation that describes electrostatic interactions between molecules in ionic solutions. It is the mathematical base for the Gouy–Chapman double layer theory; first proposed by Gouy in 1910 and complemented by Chapman in 1913...
results. The Poisson–Boltzmann equation plays a role in the development of the Debye–Hückel theory of dilute electrolyte solutions.
(Note: Although the above discussion assumes that the magnetic field is not varying in time, the same Poisson equation arises even if it does vary in time, as long as the Coulomb gauge is used. However, in this more general context, computing
is no longer sufficient to calculate , since the latter also depends on the magnetic vector potential, which must be independently computed.)Potential of a Gaussian charge density
If there is a static spherically symmetric Gaussian charge density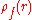:where Q is the total charge,
then the solution φ (r) of Poisson's equation,
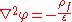,is given by
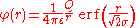
where erf(x) is the error function
Error function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
.
This solution can be checked explicitly by evaluating
.Note that, for r much greater than σ, the erf function approaches unity and the potential φ (r) approaches the point charge potential
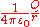, as one would expect. Furthermore the erf function approaches 1 extremely quickly as its argument increases; in practice for r > 3σ the relative error is smaller than one part in a thousand.Dynamics
In the case of a gravitational field G given by the gravitational potential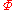 with a mass density 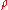:See also
- Discrete Poisson equationDiscrete Poisson equationIn mathematics, the discrete Poisson equation is the finite difference analog of the Poisson equation. In it, the discrete Laplace operator takes the place of the Laplace operator...
- Poisson–Boltzmann equation
- Uniqueness theorem for Poisson's equation
External links
- Poisson's equation on PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...
. - Poisson's Equation for a Point Source in the COMSOL MultiphysicsCOMSOL MultiphysicsCOMSOL Multiphysics is a finite element analysis, solver and Simulation software / FEA Software package for various physics and engineering applications, especially coupled phenomena, or multiphysics. COMSOL Multiphysics also offers an extensive interface to MATLAB and its toolboxes for a large...
model gallery. - Poisson's Equation Poisson's Equation video