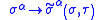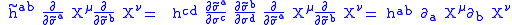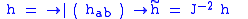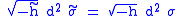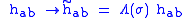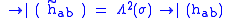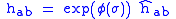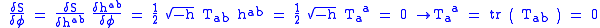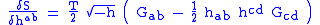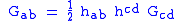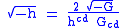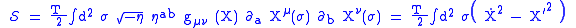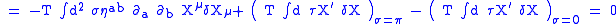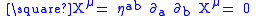Polyakov action
Encyclopedia
In physics
, the Polyakov action is the two-dimensional action
of a conformal field theory
describing the worldsheet
of a string in string theory
. It was introduced by S.Deser
and B.Zumino
and independently by L.Brink, P.Di Vecchia and P.S.Howe (in Physics Letters B65, pgs 369 and 471 respectively), and has become associated with Alexander Polyakov after he made use of it in quantizing the string. The action reads
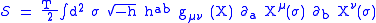
where
is the string tension
,
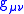is the metric of the target manifold, 
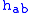is the worldsheet metric and 
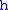is the determinant of 
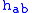. The metric signature
is chosen such that timelike directions are + and the spacelike directions are -. The spacelike worldsheet coordinate is called
wheareas the timelike worldsheet coordinate is called 
. This is also known as nonlinear sigma model.
The Polyakov action must be supplememted by the
Liouville action to describe properly string fluctuations.
The action is invariant
under spacetime translation
s and infinitesimal
Lorentz transformation
s: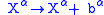
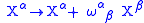
where
and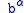 
is a constant. This forms the Poincaré symmetry
of the target manifold.
The invariance under (i) follows since the action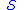
depends only on the first derivative of 
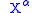. The proof of the invariance under (ii) is as follows:
|
|
|-
|
|
|-
|
|
|}
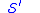
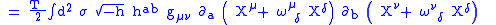
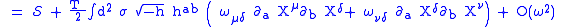
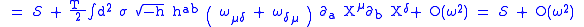
under worldsheet diffeomorphism
s (or coordinates transformations) and Weyl transformations.
It transforms the Metric tensor
in the following way:
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the Polyakov action is the two-dimensional action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
of a conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
describing the worldsheet
Worldsheet
In string theory, a worldsheet is a two-dimensional manifold which describes the embedding of a string in spacetime. The term was coined by Leonard Susskind around 1967 as a direct generalization of the world line concept for a point particle in special and general relativity.The type of string,...
of a string in string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
. It was introduced by S.Deser
Stanley Deser
Stanley Deser is an American physicist known for his contributions to general relativity. Currently, he is the Ancell Professor of Physics at Brandeis University in Waltham, Massachusetts....
and B.Zumino
Bruno Zumino
Bruno Zumino is an Italian theoretical physicist and emeritus faculty at the University of California, Berkeley. He got his bachelor degree from the University of Rome in 1945...
and independently by L.Brink, P.Di Vecchia and P.S.Howe (in Physics Letters B65, pgs 369 and 471 respectively), and has become associated with Alexander Polyakov after he made use of it in quantizing the string. The action reads
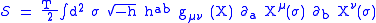
where
is the string tensionTension (mechanics)
In physics, tension is the magnitude of the pulling force exerted by a string, cable, chain, or similar object on another object. It is the opposite of compression. As tension is the magnitude of a force, it is measured in newtons and is always measured parallel to the string on which it applies...
,
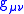is the metric of the target manifold, 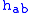is the worldsheet metric and 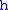is the determinant of 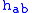. The metric signatureMetric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
is chosen such that timelike directions are + and the spacelike directions are -. The spacelike worldsheet coordinate is called
wheareas the timelike worldsheet coordinate is called . This is also known as nonlinear sigma model.The Polyakov action must be supplememted by the
Liouville action to describe properly string fluctuations.
Global symmetries
N.B. : Here, a symmetry is said to be local or global from the two dimensional theory (on the worldsheet) point of view. For example, Lorentz transformations, that are local symmetries of the space-time, are global symmetries of the theory on the worldsheet.The action is invariant
Invariant (physics)
In mathematics and theoretical physics, an invariant is a property of a system which remains unchanged under some transformation.-Examples:In the current era, the immobility of polaris under the diurnal motion of the celestial sphere is a classical illustration of physical invariance.Another...
under spacetime translation
Translation
Translation is the communication of the meaning of a source-language text by means of an equivalent target-language text. Whereas interpreting undoubtedly antedates writing, translation began only after the appearance of written literature; there exist partial translations of the Sumerian Epic of...
s and infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s:
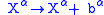
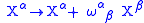
where
and 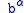is a constant. This forms the Poincaré symmetryPoincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
of the target manifold.
The invariance under (i) follows since the action
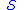depends only on the first derivative of 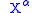. The proof of the invariance under (ii) is as follows:|
|
|-
|
|
|-
|
|
|}
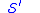
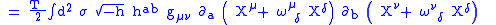
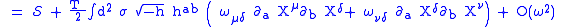
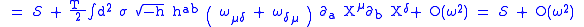
Local symmetries
The action is invariantInvariant
Invariant and invariance may have several meanings, among which are:- Computer science :* Invariant , an Expression whose value doesn't change during program execution* A type in overriding that is neither covariant nor contravariant...
under worldsheet diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s (or coordinates transformations) and Weyl transformations.
Diffeomorphisms
Assume the following transformation:
It transforms the Metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
in the following way:
-
One can see that:
One knows that the JacobianJacobianIn vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
of this transformation is given by:
which leads to:
and one sees that:
summing up this transformation leaves the action invariant.
Weyl transformation
Assume the Weyl transformation:
then:
And finally:
|
|
|-
|
|
|}
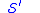
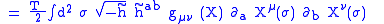
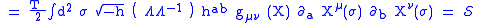
And one can see that the action is invariant under Weyl transformation. If we consider n-dimensional (spatially) extended objects whose action is proportional to their worldsheet area/hyperarea, unless n=1, the corresponding Polyakov action would contain another term breaking Weyl symmetry.
One can define the Stress-energy tensorStress-energy tensorThe stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
:
Let's define:
Because of Weyl symmetry the action does not depend on
:
Relation with Nambu-Goto action
Writing the Euler-Lagrange equationEuler-Lagrange equationIn calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
for the metric tensorMetric tensorIn the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
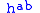one obtains that:
Knowing also that:
One can write the variational derivative of the action:
where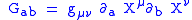
which leads to:
If the auxiliary worldsheetWorldsheetIn string theory, a worldsheet is a two-dimensional manifold which describes the embedding of a string in spacetime. The term was coined by Leonard Susskind around 1967 as a direct generalization of the world line concept for a point particle in special and general relativity.The type of string,...
metric tensorMetric tensorIn the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
is calculated from the equations of motion:
and substituted back to the action, it becomes the Nambu-Goto actionNambu-Goto actionThe Nambu–Goto action is the simplest invariant action in bosonic string theory, and is also used in other theories that investigate string-like objects . It is the starting point of the analysis of zero-thickness string behavior, using the principles of Lagrangian mechanics...
:
However, the Polyakov action is more easily quantizedQuantization (physics)In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
because it is linearLinearIn mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
.
Equations of motion
Using diffeomorphismDiffeomorphismIn mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s and Weyl transformation, with a Minkowskian target spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, one can transform the action into the following form:
where
Keeping in mind that
one can derive the constraints:
-
.
Substituting
one obtains:
And consequently:
With the boundary conditions in order to satisfy the second part of the variation of the action.- Closed strings
- Periodic boundary conditionsPeriodic boundary conditionsIn mathematical models and computer simulations, periodic boundary conditions are a set of boundary conditions that are often used to simulate a large system by modelling a small part that is far from its edge...
:
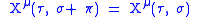
- Open strings Neumann boundary conditions:
Dirichlet boundary conditions: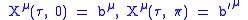 
- Open strings Neumann boundary conditions:
-
