
Polynomial function theorems for zeros
Encyclopedia
Polynomial function theorems for zeros are a set of theorem
s aiming to find (or determine the nature) of the complex zeros
of a polynomial function.
Found in most precalculus textbooks, these theorems include:
of the form
where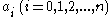 are complex number
are complex number
s and .
.
If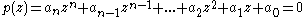 , then
, then  is called a zero of
is called a zero of 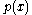 . If
. If  is real, then
is real, then  is a real zero of
is a real zero of  ; if
; if  is imaginary, the
is imaginary, the  is a complex zero of
is a complex zero of 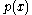 , although complex zeros include both real and imaginary zeros.
, although complex zeros include both real and imaginary zeros.
The fundamental theorem of algebra
states that every polynomial function of degree has at least one complex zero. It follows that every polynomial function of degree
has at least one complex zero. It follows that every polynomial function of degree 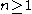 has exactly
has exactly  complex zeros, not necessarily distinct.
complex zeros, not necessarily distinct.
A degree one polynomial is also known as a linear function
, whereas a degree two polynomial is also known as a quadratic function
and its two zeros are merely a direct result of the quadratic formula. However, difficulty rises when the degree of the polynomial, n, is higher than 2. It is true that there is a cubic formula for a cubic function (a degree three polynomial) and there is a quartic formula for a quartic function (a degree four polynomial), but they are very complicated. To make matters worse, there is no general formula for a polynomial function of degree 5 or higher (see Abel–Ruffini theorem
).
 is divided by
is divided by  , then the remainder is
, then the remainder is  .
.
For example, when is divided by
is divided by  , the remainder (if we don't care about the quotient) will be
, the remainder (if we don't care about the quotient) will be 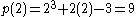 . When
. When 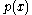 is divided by
is divided by 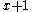 , the remainder is
, the remainder is  . However, this theorem is most useful when the remainder is 0 since it will yield a zero of
. However, this theorem is most useful when the remainder is 0 since it will yield a zero of 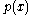 . For example,
. For example, 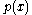 is divided by
is divided by  , the remainder is
, the remainder is  , so 1 is a zero of
, so 1 is a zero of 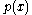 (by the definition of zero of a polynomial function).
(by the definition of zero of a polynomial function).
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s aiming to find (or determine the nature) of the complex zeros
Zero (complex analysis)
In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
of a polynomial function.
Found in most precalculus textbooks, these theorems include:
- Remainder theoremPolynomial remainder theoremIn algebra, the polynomial remainder theorem or little Bézout's theorem is an application of polynomial long division. It states that the remainder of a polynomial f\, divided by a linear divisor x-a\, is equal to f \,.- Example :...
- Factor theoremFactor theoremIn algebra, the factor theorem is a theorem linking factors and zeros of a polynomial. It is a special case of the polynomial remainder theorem.The factor theorem states that a polynomial f has a factor if and only if f=0....
- Descartes' rule of signsDescartes' rule of signsIn mathematics, Descartes' rule of signs, first described by René Descartes in his work La Géométrie, is a technique for determining the number of positive or negative real roots of a polynomial....
- Gauss–Lucas theorem
- Rational zeros theorem
- Bounds on zeros theoremExtreme value theoremIn calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...
also known as the boundedness theorem - Intermediate value theoremIntermediate value theoremIn mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
- Complex conjugate root theoremComplex conjugate root theoremIn mathematics, the complex conjugate root theorem states that if P is a polynomial in one variable with real coefficients, and a + bi is a root of P with a and b real numbers, then its complex conjugate a − bi is also a root of P.It follows from this , that if the degree...
- Properties of polynomial roots
Background
A polynomial function is a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of the form

where
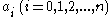 are complex number
are complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s and
 .
.If
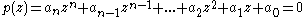 , then
, then  is called a zero of
is called a zero of 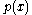 . If
. If  is real, then
is real, then  is a real zero of
is a real zero of  ; if
; if  is imaginary, the
is imaginary, the  is a complex zero of
is a complex zero of 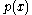 , although complex zeros include both real and imaginary zeros.
, although complex zeros include both real and imaginary zeros.The fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
states that every polynomial function of degree
 has at least one complex zero. It follows that every polynomial function of degree
has at least one complex zero. It follows that every polynomial function of degree 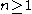 has exactly
has exactly  complex zeros, not necessarily distinct.
complex zeros, not necessarily distinct.- If the degree of the polynomial function is 1, i.e.,
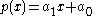 , then its (only) zero is
, then its (only) zero is 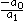 .
. - If the degree of the polynomial function is 2, i.e.,
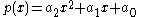 , then its two zeros (not necessarily distinct) are
, then its two zeros (not necessarily distinct) are 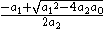 and
and 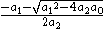 .
.
A degree one polynomial is also known as a linear function
Linear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
, whereas a degree two polynomial is also known as a quadratic function
Quadratic function
A quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....
and its two zeros are merely a direct result of the quadratic formula. However, difficulty rises when the degree of the polynomial, n, is higher than 2. It is true that there is a cubic formula for a cubic function (a degree three polynomial) and there is a quartic formula for a quartic function (a degree four polynomial), but they are very complicated. To make matters worse, there is no general formula for a polynomial function of degree 5 or higher (see Abel–Ruffini theorem
Abel–Ruffini theorem
In algebra, the Abel–Ruffini theorem states that there is no general algebraic solution—that is, solution in radicals— to polynomial equations of degree five or higher.- Interpretation :...
).
Remainder theorem
The remainder theorem states that if is divided by
is divided by  , then the remainder is
, then the remainder is  .
.For example, when
 is divided by
is divided by  , the remainder (if we don't care about the quotient) will be
, the remainder (if we don't care about the quotient) will be 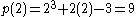 . When
. When 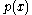 is divided by
is divided by 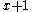 , the remainder is
, the remainder is  . However, this theorem is most useful when the remainder is 0 since it will yield a zero of
. However, this theorem is most useful when the remainder is 0 since it will yield a zero of 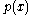 . For example,
. For example, 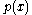 is divided by
is divided by  , the remainder is
, the remainder is  , so 1 is a zero of
, so 1 is a zero of 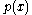 (by the definition of zero of a polynomial function).
(by the definition of zero of a polynomial function).

