Pooled variance
Encyclopedia
In statistics
, many times, data are collected for a dependent variable
, y, over a range of values for the independent variable
, x. For example, the observation of fuel consumption might be studied as a function of engine speed while the engine load is held constant. If, in order to achieve a small variance
in y, numerous repeated tests are required at each value of x, the expense of testing may become prohibitive. Reasonable estimates of variance can be determined by using the principle of pooled variance after repeating each test
at a particular x only a few times. Pooled variance is a method for estimating
variance
given several different samples
taken in different circumstances where the mean
may vary between samples but the true variance (equivalently, precision
) is assumed to remain the same. It is calculated by
or with simpler notation,
where sp2 is the pooled variance, ni is the sample size
of the ith sample, si2 is the variance of the ith sample, and k is the number of samples being combined. n − 1 is used instead of n for the same reason it may be used in estimating variances from samples (i.e. Bessel's correction
).
The square-root of a pooled variance estimator is known as a pooled standard deviation.
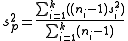
and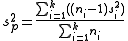
are used in different contexts. The former can give an unbiased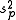
to estimate 
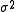when the two groups share an equal population variance. The latter one can give a more efficient 
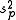to estimate 
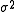biasedly. Note that the quantities 
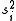in the right hand sides of both equations are the unbiased estimates.
The number of trials, mean, variance and standard deviation are presented in the next table.
These statistics represent the variance and standard deviation
for each subset of data at the various levels of x. If we can assume that the same phenomena are generating random error
at every level of x, the above data can be “pooled” to express a single estimate of variance and standard deviation. In a sense, this suggests finding a mean
variance or standard deviation among the five results above. This mean variance is calculated by weighting the individual values with the size of the subset for each level of x. Thus, the pooled variance is defined by
where n1, n2, . . . nk are the sizes of the data subsets at each level of the variable x, and S12, S22, . . ., Sk2 are their respective variances.
The pooled variance of the data shown above is therefore:
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, many times, data are collected for a dependent variable
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
, y, over a range of values for the independent variable
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
, x. For example, the observation of fuel consumption might be studied as a function of engine speed while the engine load is held constant. If, in order to achieve a small variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
in y, numerous repeated tests are required at each value of x, the expense of testing may become prohibitive. Reasonable estimates of variance can be determined by using the principle of pooled variance after repeating each test
Statistical hypothesis testing
A statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
at a particular x only a few times. Pooled variance is a method for estimating
Estimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
given several different samples
Sample (statistics)
In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...
taken in different circumstances where the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
may vary between samples but the true variance (equivalently, precision
Accuracy and precision
In the fields of science, engineering, industry and statistics, the accuracy of a measurement system is the degree of closeness of measurements of a quantity to that quantity's actual value. The precision of a measurement system, also called reproducibility or repeatability, is the degree to which...
) is assumed to remain the same. It is calculated by
or with simpler notation,
where sp2 is the pooled variance, ni is the sample size
Sample size
Sample size determination is the act of choosing the number of observations to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample...
of the ith sample, si2 is the variance of the ith sample, and k is the number of samples being combined. n − 1 is used instead of n for the same reason it may be used in estimating variances from samples (i.e. Bessel's correction
Bessel's correction
In statistics, Bessel's correction, named after Friedrich Bessel, is the use of n − 1 instead of n in the formula for the sample variance and sample standard deviation, where n is the number of observations in a sample: it corrects the bias in the estimation of the population variance,...
).
The square-root of a pooled variance estimator is known as a pooled standard deviation.
Unbiased least square estimate vs. biased maximum likelihood estimate
Both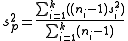and
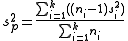
are used in different contexts. The former can give an unbiased
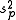to estimate 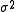when the two groups share an equal population variance. The latter one can give a more efficient 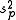to estimate 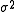biasedly. Note that the quantities 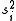in the right hand sides of both equations are the unbiased estimates.Example
Consider the following set of data for y obtained at various levels of the independent variable x.| x | y |
|---|---|
| 1 | 31, 30, 29 |
| 2 | 42, 41, 40, 39 |
| 3 | 31, 28 |
| 4 | 23, 22, 21, 19, 18 |
| 5 | 21, 20, 19, 18,17 |
The number of trials, mean, variance and standard deviation are presented in the next table.
| x | n | ymean | Sy2 | S |
|---|---|---|---|---|
| 1 | 3 | 30.0 | 1.0 | 1.0 |
| 2 | 4 | 40.5 | 1.67 | 1.29 |
| 3 | 2 | 29.5 | 4.5 | 2.12 |
| 4 | 5 | 20.6 | 4.3 | 2.07 |
| 5 | 5 | 19.0 | 2.5 | 1.58 |
These statistics represent the variance and standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
for each subset of data at the various levels of x. If we can assume that the same phenomena are generating random error
Random error
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measures of a constant attribute or quantity are taken...
at every level of x, the above data can be “pooled” to express a single estimate of variance and standard deviation. In a sense, this suggests finding a mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
variance or standard deviation among the five results above. This mean variance is calculated by weighting the individual values with the size of the subset for each level of x. Thus, the pooled variance is defined by
where n1, n2, . . . nk are the sizes of the data subsets at each level of the variable x, and S12, S22, . . ., Sk2 are their respective variances.
The pooled variance of the data shown above is therefore:
