Post-hoc analysis
Encyclopedia
Post-hoc analysis in the context of design
and analysis of experiments, refers to looking at the data—after the experiment has concluded—for patterns that were not specified a priori
. It is sometimes called by critics data dredging
to evoke the sense that the more one looks the more likely something will be found. More subtly, each time a pattern in the data is considered, a statistical test
is effectively performed. This greatly inflates the total number of statistical tests and necessitates the use of multiple testing procedures to compensate. However, this is difficult to do precisely and in fact most results of post-hoc analyses are reported as they are with unadjusted p-values
. These p-values must be interpreted in light of the fact that they are a small and selected subset of a potentially large group of p-values. Results of post-hoc analysis should be explicitly labeled as such in reports and publications to avoid misleading readers.
In practice, post-hoc analyses are usually concerned with finding patterns and/or relationships between subgroups
of sampled populations
that would otherwise remain undetected and undiscovered were a scientific community to rely strictly upon a priori
statistical methods. Post-hoc tests — also known as a posteriori tests — greatly expand the range and capability of methods that can be applied in exploratory research
. Post-hoc examination strengthens induction
by limiting the probability that significant effects will seem to have been discovered between subgroups of a population when none actually exist. As it is, many scientific papers are published without adequate, preventative post-hoc control of the Type I Error Rate.
Post-hoc analysis is an important procedure without which multivariate hypothesis testing would greatly suffer, rendering the chances of discovering false positives unacceptably high. Ultimately, post-hoc testing creates better informed scientists who can therefore formulate better, more efficient a priori hypotheses and research designs.
An example of an analysis often mislabeled as a post-hoc analysis is the Newman–Keuls method
: "A different approach to evaluating a posteriori pairwise comparisons stems from the work of Student (1927), Newman (1939), and Keuls (1952). The Newman–Keuls procedure is based on a stepwise or layer approach to significance testing. Sample means are ordered from the smallest to the largest. The largest difference, which involves means that are r = p steps apart, is tested first at α level of significance; if significant, means that are r = p − 1 steps apart are tested at α level of significance and so on. The Newman–Keuls procedure provides an r-mean significance level equal to α for each group of r ordered means, that is, the probability of falsely rejecting the hypothesis that all means in an ordered group are equal to α. It follows that the concept of error rate applies neither on an experimentwise nor on a per comparison basis–the actual error rate falls somewhere between the two. The Newman–Keuls procedure, like Tukey's procedure, requires equal sample n' s.
The critical difference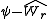
, that two means separated by r steps must exceed to be declared significant is, according to the Newman–Keuls procedure,
The Newman–Keuls and Tukey procedures require the same critical difference for the first comparison that is tested. The Tukey procedure uses this critical difference for all the remaining tests, whereas the Newman–Keuls procedure reduces the size of the critical difference, depending on the number of steps separating the ordered means. As a result, the Newman–Keuls test is more powerful than Tukey's test. Remember, however, that the Newman–Keuls procedure does not control the experimentwise error rate at α.
Frequently a test of the overall null hypothesis m1 = m2 = … = mp is performed with an F statistic in ANOVA rather than with a range statistic. If the F statistic is significant, Shaffer (1979) recommends using the critical difference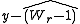
instead of 
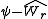to evaluate the largest pairwise comparison at the first step of the testing procedure. The testing procedure for all subsequent steps is unchanged. She has shown that the modified procedure leads to greater power at the first step without affecting control of the type I error rate. This makes dissonances, in which the overall null hypothesis is rejected by an F test without rejecting any one of the proper subsets of comparison, less likely."
Design of experiments
In general usage, design of experiments or experimental design is the design of any information-gathering exercises where variation is present, whether under the full control of the experimenter or not. However, in statistics, these terms are usually used for controlled experiments...
and analysis of experiments, refers to looking at the data—after the experiment has concluded—for patterns that were not specified a priori
A priori (statistics)
In statistics, a priori knowledge is prior knowledge about a population, rather than that estimated by recent observation. It is common in Bayesian inference to make inferences conditional upon this knowledge, and the integration of a priori knowledge is the central difference between the Bayesian...
. It is sometimes called by critics data dredging
Data dredging
Data dredging is the inappropriate use of data mining to uncover misleading relationships in data. Data-snooping bias is a form of statistical bias that arises from this misuse of statistics...
to evoke the sense that the more one looks the more likely something will be found. More subtly, each time a pattern in the data is considered, a statistical test
Statistical hypothesis testing
A statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
is effectively performed. This greatly inflates the total number of statistical tests and necessitates the use of multiple testing procedures to compensate. However, this is difficult to do precisely and in fact most results of post-hoc analyses are reported as they are with unadjusted p-values
P-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
. These p-values must be interpreted in light of the fact that they are a small and selected subset of a potentially large group of p-values. Results of post-hoc analysis should be explicitly labeled as such in reports and publications to avoid misleading readers.
In practice, post-hoc analyses are usually concerned with finding patterns and/or relationships between subgroups
Sample (statistics)
In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...
of sampled populations
Statistical population
A statistical population is a set of entities concerning which statistical inferences are to be drawn, often based on a random sample taken from the population. For example, if we were interested in generalizations about crows, then we would describe the set of crows that is of interest...
that would otherwise remain undetected and undiscovered were a scientific community to rely strictly upon a priori
A priori (statistics)
In statistics, a priori knowledge is prior knowledge about a population, rather than that estimated by recent observation. It is common in Bayesian inference to make inferences conditional upon this knowledge, and the integration of a priori knowledge is the central difference between the Bayesian...
statistical methods. Post-hoc tests — also known as a posteriori tests — greatly expand the range and capability of methods that can be applied in exploratory research
Exploratory research
Exploratory research is a type of research conducted for a problem that has not been clearly defined. Exploratory research helps determine the best research design, data collection method and selection of subjects. It should draw definitive conclusions only with extreme caution...
. Post-hoc examination strengthens induction
Inductive reasoning
Inductive reasoning, also known as induction or inductive logic, is a kind of reasoning that constructs or evaluates propositions that are abstractions of observations. It is commonly construed as a form of reasoning that makes generalizations based on individual instances...
by limiting the probability that significant effects will seem to have been discovered between subgroups of a population when none actually exist. As it is, many scientific papers are published without adequate, preventative post-hoc control of the Type I Error Rate.
Post-hoc analysis is an important procedure without which multivariate hypothesis testing would greatly suffer, rendering the chances of discovering false positives unacceptably high. Ultimately, post-hoc testing creates better informed scientists who can therefore formulate better, more efficient a priori hypotheses and research designs.
Student Neuman–Keuls post-hoc ANOVA
The Student Newman–Keuls and related tests are often referred to as post hoc. However, an experimenter often plans to test all pairwise comparisons before seeing the data. Therefore these tests are better categorized as a priori.An example of an analysis often mislabeled as a post-hoc analysis is the Newman–Keuls method
Newman–Keuls method
In statistics, the Newman–Keuls method is a post-hoc test used for comparisons after the performed F-test is found to be significant...
: "A different approach to evaluating a posteriori pairwise comparisons stems from the work of Student (1927), Newman (1939), and Keuls (1952). The Newman–Keuls procedure is based on a stepwise or layer approach to significance testing. Sample means are ordered from the smallest to the largest. The largest difference, which involves means that are r = p steps apart, is tested first at α level of significance; if significant, means that are r = p − 1 steps apart are tested at α level of significance and so on. The Newman–Keuls procedure provides an r-mean significance level equal to α for each group of r ordered means, that is, the probability of falsely rejecting the hypothesis that all means in an ordered group are equal to α. It follows that the concept of error rate applies neither on an experimentwise nor on a per comparison basis–the actual error rate falls somewhere between the two. The Newman–Keuls procedure, like Tukey's procedure, requires equal sample n
The critical difference
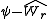, that two means separated by r steps must exceed to be declared significant is, according to the Newman–Keuls procedure,
The Newman–Keuls and Tukey procedures require the same critical difference for the first comparison that is tested. The Tukey procedure uses this critical difference for all the remaining tests, whereas the Newman–Keuls procedure reduces the size of the critical difference, depending on the number of steps separating the ordered means. As a result, the Newman–Keuls test is more powerful than Tukey's test. Remember, however, that the Newman–Keuls procedure does not control the experimentwise error rate at α.
Frequently a test of the overall null hypothesis m1 = m2 = … = mp is performed with an F statistic in ANOVA rather than with a range statistic. If the F statistic is significant, Shaffer (1979) recommends using the critical difference
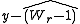instead of 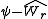to evaluate the largest pairwise comparison at the first step of the testing procedure. The testing procedure for all subsequent steps is unchanged. She has shown that the modified procedure leads to greater power at the first step without affecting control of the type I error rate. This makes dissonances, in which the overall null hypothesis is rejected by an F test without rejecting any one of the proper subsets of comparison, less likely."List of post-hoc tests
- Fisher's least significant difference (LSD)
- Bonferroni correctionBonferroni correctionIn statistics, the Bonferroni correction is a method used to counteract the problem of multiple comparisons. It was developed and introduced by Italian mathematician Carlo Emilio Bonferroni...
- Duncan's new multiple range testDuncan's new multiple range testIn statistics, Duncan's new multiple range test is a multiple comparison procedure developed by David B. Duncan in 1955. Duncan's MRT belongs to the general class of multiple comparison procedures that use the studentized range statistic qr to compare sets of means.Duncan's new multiple range test...
- Friedman testFriedman testThe Friedman test is a non-parametric statistical test developed by the U.S. economist Milton Friedman. Similar to the parametric repeated measures ANOVA, it is used to detect differences in treatments across multiple test attempts. The procedure involves ranking each row together, then...
- Newman–Keuls methodNewman–Keuls methodIn statistics, the Newman–Keuls method is a post-hoc test used for comparisons after the performed F-test is found to be significant...
- Scheffé's methodScheffé's methodIn statistics, Scheffé's method, named after Henry Scheffé, is a method for adjusting significance levels in a linear regression analysis to account for multiple comparisons...
- Tukey's range test
See also
- ANOVA
- The significance level α (alpha) in statistical hypothesis testingStatistical hypothesis testingA statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
- Subgroup analysisSubgroup analysisSubgroup analysis, in the context of design and analysis of experiments, refers to looking for pattern in a subset of the subjects....
- Post hoc ergo propter hocPost hoc ergo propter hocPost hoc ergo propter hoc, Latin for "after this, therefore because of this," is a logical fallacy that states, "Since that event followed this one, that event must have been caused by this one." It is often shortened to simply post hoc and is also sometimes referred to as false cause,...