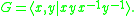In geometric group theory

Geometric group theory

Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...

, a presentation complex is a 2-dimensional cell complex associated to any presentation

Presentation of a group

In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...

 of a group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

 G. The complex has a single vertex, and one loop at the vertex for each generator

Generating set of a group

In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...

 of G. There is one 2-cell for each relation in the presentation, with the boundary of the 2-cell attached along the appropriate word.

Properties

• The fundamental group
  Fundamental group
  In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
  
   of the presentation complex is the group G itself.
• The universal cover of the presentation complex is a Cayley complex for G, whose 1-skeleton is the Cayley graph
  Cayley graph
  In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
  
   of G.
• Any presentation complex for G is the 2-skeleton of an Eilenberg–Maclane space K(G,1).

Example

Let G =Z² be the two-dimensional integer lattice

Lattice (group)

In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...

, with a presentation

Then the presentation complex for G is a torus

Torus

In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...

, obtained by gluing the opposite sides of a square, the 2-cell, which are labelled x and y. All four corners of the square are glued into a single vertex, the 0-cell of the presentation complex, while a pair consisting of a longtitudal and meridian circles on the torus, intersecting at the vertex, constitutes its 1-skeleton.

The associated Cayley complex is a regular tiling of the plane

Plane (mathematics)

In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...

by unit squares. The 1-skeleton of this complex is a Cayley graph for Z².