
Product of group subsets
Encyclopedia
In mathematics
, one can define a product of group subsets in a natural way. If S and T are subset
s of a group
G then their product is the subset of G defined by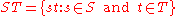
Note that S and T need not be subgroup
s. The associativity
of this product follows from that of the group product. The product of group subsets therefore defines a natural monoid
structure on the power set of G.
If S and T are subgroups of G their product need not be a subgroup. It will be a subgroup if and only if ST = TS and the two subgroups are said to permute. In this case ST is the group generated
by S and T, i.e. ST = TS = <S ∪ T>. If either S or T is normal
then this condition is satisfied and ST is a subgroup. Suppose S is normal. Then according to the second isomorphism theorem S ∩ T is normal in T and ST/S ≅ T/(S ∩ T).
If G is a finite group and S and T and subgroups of G then ST is a subset of G of size |ST| given by the product formula: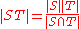
Note that this applies even if neither S nor T is normal.
In particular, if S and T (subgroups now) intersect only in the identity, then every element of ST has a unique expression as a product st with s in S and t in T. If S and T also permute, then ST is a group, and is called a Zappa-Szep product
. Even further, if S or T is normal in ST, then ST is called a semidirect product
. Finally, if both S and T are normal in ST, then ST is called a direct product
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, one can define a product of group subsets in a natural way. If S and T are subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G then their product is the subset of G defined by
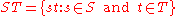
Note that S and T need not be subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s. The associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
of this product follows from that of the group product. The product of group subsets therefore defines a natural monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
structure on the power set of G.
If S and T are subgroups of G their product need not be a subgroup. It will be a subgroup if and only if ST = TS and the two subgroups are said to permute. In this case ST is the group generated
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
by S and T, i.e. ST = TS = <S ∪ T>. If either S or T is normal
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
then this condition is satisfied and ST is a subgroup. Suppose S is normal. Then according to the second isomorphism theorem S ∩ T is normal in T and ST/S ≅ T/(S ∩ T).
If G is a finite group and S and T and subgroups of G then ST is a subset of G of size |ST| given by the product formula:
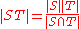
Note that this applies even if neither S nor T is normal.
In particular, if S and T (subgroups now) intersect only in the identity, then every element of ST has a unique expression as a product st with s in S and t in T. If S and T also permute, then ST is a group, and is called a Zappa-Szep product
Zappa-Szep product
In mathematics, especially group theory, the Zappa–Szép product describes a way in which a group can be constructed from two subgroups. It is a generalization of the direct and semidirect products...
. Even further, if S or T is normal in ST, then ST is called a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
. Finally, if both S and T are normal in ST, then ST is called a direct product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
.

