
Projective set
Encyclopedia
In the mathematical field of descriptive set theory
, a subset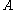 of a Polish space
of a Polish space
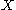 is projective if it is
is projective if it is 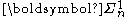 for some positive integer
for some positive integer  . Here
. Here 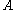 is
is
The choice of the Polish space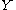 in the third clause above is not very important; it could be replaced in the definition by a fixed uncountable Polish space, say Baire space
in the third clause above is not very important; it could be replaced in the definition by a fixed uncountable Polish space, say Baire space
or Cantor space
or the real line
.
on subsets of Baire space and the projective hierarchy on subsets of Baire space. Not every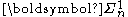 subset of Baire space is
subset of Baire space is 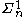 . It is true, however, that if a subset X of Baire space is
. It is true, however, that if a subset X of Baire space is 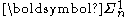 then there is a set of natural numbers A such that X is
then there is a set of natural numbers A such that X is 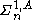 . A similar statement holds for
. A similar statement holds for 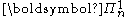 sets. Thus the sets classified by the projective hierarchy are exactly the sets classified by the relativized version of the analytical hierarchy. This relationship is important in effective descriptive set theory
sets. Thus the sets classified by the projective hierarchy are exactly the sets classified by the relativized version of the analytical hierarchy. This relationship is important in effective descriptive set theory
.
A similar relationship between the projective hierarchy and the relativized analytical hierarchy holds for subsets of Cantor space and, more generally, subsets of any effective Polish space
.
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
, a subset
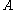 of a Polish space
of a Polish spacePolish space
In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
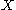 is projective if it is
is projective if it is 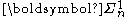 for some positive integer
for some positive integer  . Here
. Here 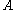 is
is
-
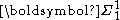 if
if  is analyticAnalytic setIn descriptive set theory, a subset of a Polish space X is an analytic set if it is a continuous image of a Polish space. These sets were first defined by and his student .- Definition :There are several equivalent definitions of analytic set...
is analyticAnalytic setIn descriptive set theory, a subset of a Polish space X is an analytic set if it is a continuous image of a Polish space. These sets were first defined by and his student .- Definition :There are several equivalent definitions of analytic set... -
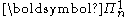 if the complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
if the complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of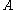 ,
,  , is
, is 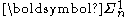
-
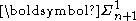 if there is a Polish space
if there is a Polish space 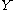 and a
and a 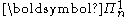 subset
subset 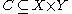 such that
such that 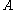 is the projection of
is the projection of 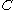 ; that is,
; that is, 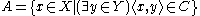
The choice of the Polish space
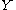 in the third clause above is not very important; it could be replaced in the definition by a fixed uncountable Polish space, say Baire space
in the third clause above is not very important; it could be replaced in the definition by a fixed uncountable Polish space, say Baire spaceBaire space (set theory)
In set theory, the Baire space is the set of all infinite sequences of natural numbers with a certain topology. This space is commonly used in descriptive set theory, to the extent that its elements are often called “reals.” It is often denoted B, N'N, or ωω...
or Cantor space
Cantor space
In mathematics, a Cantor space, named for Georg Cantor, is a topological abstraction of the classical Cantor set: a topological space is a Cantor space if it is homeomorphic to the Cantor set. In set theory, the topological space 2ω is called "the" Cantor space...
or the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
.
Relationship to the analytical hierarchy
There is a close relationship between the relativized analytical hierarchyAnalytical hierarchy
In mathematical logic and descriptive set theory, the analytical hierarchy is a higher type analogue of the arithmetical hierarchy. It thus continues the classification of sets by the formulas that define them.-The analytical hierarchy of formulas:...
on subsets of Baire space and the projective hierarchy on subsets of Baire space. Not every
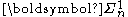 subset of Baire space is
subset of Baire space is 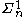 . It is true, however, that if a subset X of Baire space is
. It is true, however, that if a subset X of Baire space is 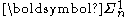 then there is a set of natural numbers A such that X is
then there is a set of natural numbers A such that X is 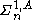 . A similar statement holds for
. A similar statement holds for 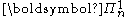 sets. Thus the sets classified by the projective hierarchy are exactly the sets classified by the relativized version of the analytical hierarchy. This relationship is important in effective descriptive set theory
sets. Thus the sets classified by the projective hierarchy are exactly the sets classified by the relativized version of the analytical hierarchy. This relationship is important in effective descriptive set theoryEffective descriptive set theory
Effective descriptive set theory is the branch of descriptive set theory dealing with sets of reals having lightface definitions; that is, definitions that do not require an arbitrary real parameter. Thus effective descriptive set theory combines descriptive set theory with recursion theory....
.
A similar relationship between the projective hierarchy and the relativized analytical hierarchy holds for subsets of Cantor space and, more generally, subsets of any effective Polish space
Effective Polish space
In mathematical logic, an effective Polish space is a complete separable metric space that has a computable presentation. Such spaces are studied in effective descriptive set theory and in constructive analysis.- Definition :...
.

