Proper velocity
Encyclopedia
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
for measuring motion. Whereas velocity relative to an observer is distance per unit time where both distance and time are measured by the observer, proper velocity relative to an observer divides observer-measured distance by the time elapsed on the clocks of the traveling object. Proper velocity equals velocity at low speeds. Proper velocity at high speeds, moreover, retains many of the properties that velocity loses in relativity compared with Newtonian theory.
For example proper-velocity equals momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
per unit mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
at any speed, and therefore has no upper limit. At high speeds, as shown in the figure at right, it is proportional to an object's energy as well.
Proper-velocity is one of three related derivatives in special relativity (coordinate velocity v = dx/dt, proper-velocity w = dx/dτ, and Lorentz factor
Lorentz factor
The Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
γ = dt/dτ) that describe an object's rate of travel. For unidirectional motion, each of these is also simply related to a traveling object's hyperbolic velocity angle or rapidity
Rapidity
In relativity, rapidity is an alternative to speed as a framework for measuring motion. On parallel velocities rapidities are simply additive, unlike speeds at relativistic velocities. For low speeds, rapidity and speed are proportional, but for high speeds, rapidity takes a larger value. The...
η by
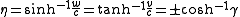.Introduction
In flat spacetime, proper-velocity is the ratio between distance traveled relative to a reference map-frame (used to define simultaneity) and proper timeProper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
τ elapsed on the clocks of the traveling object. It equals the object's momentum p divided by its rest mass m, and is made up of the space-like components of the object's four-vector
Four-vector
In the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
velocity. William Shurcliff's monograph mentioned its early use in the Sears and Brehme text. Fraundorf has explored its pedagogical value while Ungar, Baylis and Hestenes have examined its relevance from group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
and geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
perspectives. Proper-velocity is sometimes referred to as celerity.
Unlike the more familiar coordinate velocity v, proper-velocity is useful for describing both super-relativistic and sub-relativistic motion. Like coordinate velocity and unlike four-vector velocity, it resides in the three-dimensional slice of spacetime defined by the map-frame. This makes it more useful for map-based (e.g. engineering) applications, and less useful for gaining coordinate-free insight. Proper-speed divided by lightspeed c is the hyperbolic sine of rapidity η, just as the Lorentz factor γ is rapidity's hyperbolic cosine, and coordinate speed v over lightspeed is rapidity's hyperbolic tangent.
Imagine an object traveling through a region of space-time locally described by Hermann Minkowski
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
's flat-space metric equation (cdτ)2 = (cdt)2 - (dx)2. Here a reference map frame of yardsticks and synchronized clocks define map position x and map time t respectively, and the d preceding a coordinate means infinitesimal change. A bit of manipulation allows one to show that proper-velocity w = dx/dτ = γv where as usual coordinate velocity v = dx/dt. Thus finite w ensures that v is less than lightspeed c. By grouping γ with v in the expression for relativistic momentum p, proper velocity also extends the Newtonian form of momentum as mass times velocity to high speeds without a need for relativistic mass.
Proper velocity addition formula
The proper velocity addition formula: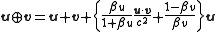
where
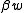is the beta factor given by 
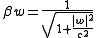.This formula provides a proper-velocity gyrovector space
Gyrovector space
A gyrovector space is a mathematical concept for studying hyperbolic geometry in analogy to the way vector spaces are used in Euclidean geometry. This vector-based approach has been developed by Abraham Albert Ungar from the late 1980s onwards...
model of hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
that uses a whole space compared to other models of hyperbolic geometry which use discs or half-planes.
In the unidirectional case this becomes commutative and simplifies to a Lorentz-factor product times a coordinate-velocity sum, e.g. to wAC = γABγBC(vAB+vBC), as discussed in the application section below.
speed table
The table below illustrates how the proper-velocity of w=c or "one map-lightyear per traveler-year" is a natural benchmark for the transition from sub-relativistic to super-relativistic motion.| Condition\Parameter | Coordinate velocity v dx/dt in units of c | Velocity angle η in i-radians | | Proper velocity w dx/dτ in units of c | Lorentz factor γ dt/dτ = E/mc2 |
|---|---|---|---|---|
| Traveler stopped in map-frame ⇔ 1 map-year/traveler-year |
0 | 0 | 0 | 1 |
| Momentum = ½mc ⇔ 0.5 map-lightyear/traveler-year |
1/√5 ≅ 0.447 | ln[(1+√5)/2] ≅ 0.481 | ½ | √5/2 ≅ 1.118 |
| Rapidity of 0.5 hyperbolic radian | (e-1)/(e+1) ≅ 0.462 | ½ | ½(√e-1/√e) ≅ 0.521 | ½(√e+1/√e) ≅ 1.128 |
| Coordinate velocity = ½ c ⇔ 0.5 map-lightyear/map-year |
½ | ½ln[3] ≅ 0.549 | 1/√3 ≅ 0.577 | 2/√3 ≅ 1.155 |
| Momentum = mc ⇔ 1 map-lightyear/traveler-year |
1/√2 ≅ 0.707 | ln[1+√2] ≅ 0.881 | 1 | √2 ≅ 1.414 |
| Rapidity of 1 hyperbolic radian | (e2-1)/(e2+1) ≅ 0.761 | 1 | ½(e-1/e) ≅ 1.175 | ½(e+1/e) ≅ 1.543 |
| Kinetic energy = mc2 ⇔ 2 map-years/traveler-year |
√3/2 ≅ 0.866 | ln[√3+2] ≅ 1.317 | √3 ≅ 1.732 | 2 |
| Momentum = 2mc ⇔ 2 map-lightyears/traveler-year |
2/√5 ≅ 0.894 | ln[2+√5] ≅ 1.444 | 2 | √5 ≅ 2.236 |
| Rapidity of 2 hyperbolic radians | (e4-1)/(e4+1) ≅ 0.964 | 2 | ½(e2-1/e2) ≅ 3.627 | ½(e2+1/e2) ≅ 3.762 |
| Coordinate velocity = c ⇔ 1 map-lightyear/map-year |
1 | ∞ | ∞ | ∞ |
Note from above that velocity angle η and proper-velocity w run from 0 to infinity and track coordinate-velocity when w<
interconversion equations
The following equations convert between four alternate measures of speed (or unidirectional velocity) that flow from Minkowski's flat-space metric-equation: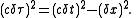
.Lorentz factor γ: Energy over mc2 ≥ 1
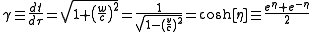
proper-velocity w: Momentum per unit mass
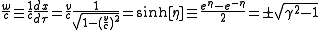
coordinate velocity: v ≤ c
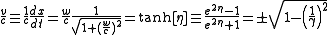
hyperbolic velocity angle or rapidity
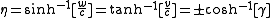
or in terms of logarithms:
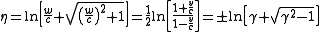.Comparing velocities at high speed
For example, a 45 GeV electron accelerated by the Large Electron-Positron Collider
Large Electron-Positron Collider
The Large Electron–Positron Collider was one of the largest particle accelerators ever constructed.It was built at CERN, a multi-national centre for research in nuclear and particle physics near Geneva, Switzerland. LEP was a circular collider with a circumference of 27 kilometres built in a...
(LEP) at Cern in 1989 would have had a Lorentz factor γ of about 88,000 (90 GeV divided by the electron rest mass of 511 keV). Its coordinate speed v would have been about sixty four trillionths shy of lightspeed c at 1 lightsecond per map second. On the other hand, its proper-speed would have been w = γv ~88,000 lightseconds per traveler second. By comparison the coordinate speed of a 250 GeV electron in the proposed International Linear Collider
International Linear Collider
The International Linear Collider is a proposed linear particle accelerator. It is planned to have a collision energy of 500 GeV initially, and, if approved after the project has published its Technical Design Report, planned for 2012, could be completed in the late 2010s. A later upgrade to 1000...
(ILC) will remain near c, while its proper-speed will significantly increase to ~489,000 lightseconds per traveler second.
Proper-velocity is also useful for comparing relative velocities along a line at high speed. In this case
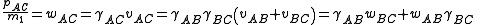
where A, B and C refer to different objects or frames of reference. For example wAC refers to the proper-speed of object A with respect to object C. Thus in calculating the relative proper-speed, Lorentz factors multiply when coordinate speeds add.
Hence each of two electrons (A and C) in a head-on collision at 45 GeV in the lab frame (B) would see the other coming toward them at vAC ~c and wAC = 88,0002(1+1) ~1.55×1010 lightseconds per traveler second. Thus from the target's point of view, colliders can explore collisions with much higher projectile energy and momentum per unit mass.
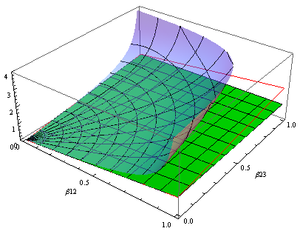
Proper-velocity-based dispersion relations
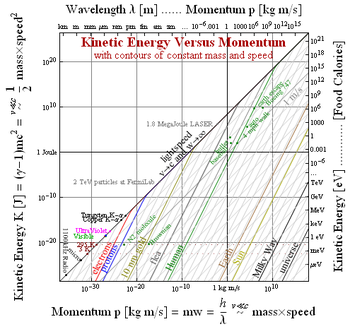
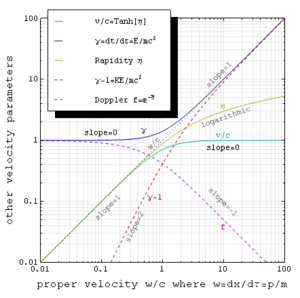
To illustrate, the figure at right with log-log axes shows objects with the same kinetic energy (horizontally related) that carry different amounts of momentum, as well as how the speed of a low-mass object compares (by vertical extrapolation) to the speed after perfectly inelastic collision with a large object at rest. Highly sloped lines (rise/run=2) mark contours of constant mass, while lines of unit slope mark contours of constant speed.
Objects that fit nicely on this plot are humans driving cars, dust particles in Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
, a spaceship in orbit around the sun, molecules at room temperature, a fighter jet at Mach 3, one radio wave photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
, a person moving at one lightyear per traveler year, the pulse of a 1.8 MegaJoule laser
Laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of photons. The term "laser" originated as an acronym for Light Amplification by Stimulated Emission of Radiation...
, a 250 GeV electron, and our observable universe with the blackbody kinetic energy expected of a single particle at 3 Kelvin.
Unidirectional acceleration via proper velocity
Proper accelerationProper acceleration
In relativity theory, proper acceleration is the physical acceleration experienced by an object. It is acceleration relative to a free-fall, or inertial, observer who is momentarily at rest relative to the object being measured...
at any speed is the physical acceleration experienced locally by an object. In spacetime its a three-vector acceleration with respect to the object's instantaneously-varying free-float frame. Its magnitude α is the frame-invariant magnitude of that object's four-acceleration
Four-acceleration
In special relativity, four-acceleration is a four-vector and is defined as the change in four-velocity over the particle's proper time:whereandand \gamma_u is the Lorentz factor for the speed u...
. Proper-acceleration is also useful from the vantage point (or spacetime slice) of external observers. Not only may observers in all frames agree on its magnitude, but it also measures the extent to which an accelerating rocket "has its pedal to the metal".
In the unidirectional case i.e. when the object's acceleration is parallel or anti-parallel to its velocity in the spacetime slice of the observer, the change in proper-velocity is the integral of proper acceleration over map-time i.e. Δw=αΔt for constant α. At low speeds this reduces to the well-known relation between coordinate velocity and coordinate acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
times map-time, i.e. Δv=aΔt. For constant unidirectional proper-acceleration, similar relationships exist between rapidity η and elapsed proper-time Δτ, as well as between Lorentz factor γ and distance traveled Δx. To be specific:
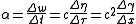,where as noted above the various velocity parameters are related by
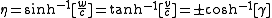.These equations describe some consequences of accelerated travel at high speed. For example, imagine a spaceship that can accelerate its passengers at "1-gee" (or 1.03 lightyears/year2) halfway to their destination, and then decelerate them at "1-gee" for the remaining half so as to provide earth-like artificial gravity from point A to point B over the shortest possible time (Brachistochrone curve
Brachistochrone curve
A Brachistochrone curve , or curve of fastest descent, is the curve between two points that is covered in the least time by a point-like body that starts at the first point with zero speed and is constrained to move along the curve to the second point, under the action of constant gravity and...
). For a map-distance of ΔxAB, the first equation above predicts a mid-point Lorentz factor (up from its unit rest value) of γmid=1+α(ΔxAB/2)/c2. Hence the round-trip time on traveler clocks will be Δτ = 4(c/α)cosh−1[γmid], during which the time elapsed on map clocks will be Δt = 4(c/α)sinh[cosh−1[γmid]].
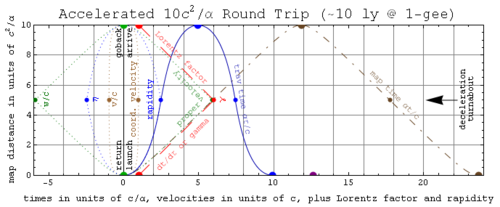
Proxima Centauri
Proxima Centauri is a red dwarf star about 4.2 light-years distant in the constellation of Centaurus. It was discovered in 1915 by Robert Innes, the Director of the Union Observatory in South Africa, and is the nearest known star to the Sun, although it is too faint to be seen with the naked eye...
lasting about 7.1 traveler years (~12 years on earth clocks), round trips to the Milky Way
Milky Way
The Milky Way is the galaxy that contains the Solar System. This name derives from its appearance as a dim un-resolved "milky" glowing band arching across the night sky...
's central black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
of about 40 years (~54,000 years elapsed on earth clocks), and round trips to Andromeda Galaxy
Andromeda Galaxy
The Andromeda Galaxy is a spiral galaxy approximately 2.5 million light-years from Earth in the constellation Andromeda. It is also known as Messier 31, M31, or NGC 224, and is often referred to as the Great Andromeda Nebula in older texts. Andromeda is the nearest spiral galaxy to the...
lasting around 57 years (over 5 million years on earth clocks). Unfortunately, sustaining 1-gee acceleration for years is easier said than done.
See also
- KinematicsKinematicsKinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
: for studying ways that position changes with time - Lorentz factorLorentz factorThe Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
: γ=dt/dτ or kinetic energy over mc2 - RapidityRapidityIn relativity, rapidity is an alternative to speed as a framework for measuring motion. On parallel velocities rapidities are simply additive, unlike speeds at relativistic velocities. For low speeds, rapidity and speed are proportional, but for high speeds, rapidity takes a larger value. The...
: hyperbolic velocity angle in imaginary radians - Four-velocityFour-velocityIn physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
: combining travel through time and space - Uniform Acceleration: holding coordinate acceleration fixed
- Gullstrand–Painlevé coordinates: free-float frames in curved space-time.
External links
- Excerpts from the first edition of Spacetime Physics, and other resources posted by Edwin F. Taylor
- William A. Shurcliff obituaries: BostonGlobe, NYtimes, WashingtonPost.