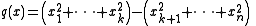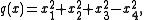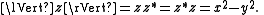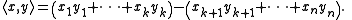Pseudo-Euclidean space
Encyclopedia
A pseudo-Euclidean space is a finite-dimension
al real
vector space
together with a non-degenerate
indefinite
quadratic form
. Such a quadratic form can, after a change of coordinates, be written as
where x = (x1, ..., xn), n is the dimension of the space, and 1 ≤ k < n. For true Euclidean space
s one has k = n, so the quadratic form is positive-definite, rather than indefinite.
A very important pseudo-Euclidean space is Minkowski space
, which is the mathematical setting in which Albert Einstein
's theory of special relativity
is conveniently formulated. For Minkowski space, n = 4 and k = 3 so that
The geometry associated with this pseudo-metric was investigated by Poincaré
who showed its consistency in spite of a total breakdown of the usual properties of Euclidean space. For example a straight line may be perpendicular to itself.
Another pseudo-Euclidean space is the plane z = x + y j consisting of split-complex number
s, equipped with the quadratic form
The magnitude of a vector x in the space is defined as q(x). In a pseudo-Euclidean space, unlike in a Euclidean space, there exist non-zero vectors with zero magnitude, and also vectors with negative magnitude.
Associated with the quadratic form q is the pseudo-Euclidean inner product
This bilinear form is symmetric, but not positive-definite, so it is not a true inner product.
Whereas Euclidean space has a unit sphere
, pseudo-Euclidean space has the hypersurface
s {x : q(x) = 1 } and {x : q(x) = −1}. Such a hypersurface, called a hyperboloid or unit quasi-sphere, is preserved by the appropriate indefinite orthogonal group.
Every pseudo-Euclidean space has a linear cone given by {x : q(x) = 0 }. When the pseudo-Euclidean space provides a model for spacetime
, the linear cone is called the light cone
of the origin.
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
together with a non-degenerate
Degenerate form
In mathematics, specifically linear algebra, a degenerate bilinear form ƒ on a vector space V is one such that the map from V to V^* given by v \mapsto is not an isomorphism...
indefinite
Definite bilinear form
In mathematics, a definite bilinear form is a bilinear form B over some vector space V such that the associated quadratic formQ=B \,...
quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
. Such a quadratic form can, after a change of coordinates, be written as
where x = (x1, ..., xn), n is the dimension of the space, and 1 ≤ k < n. For true Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s one has k = n, so the quadratic form is positive-definite, rather than indefinite.
A very important pseudo-Euclidean space is Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, which is the mathematical setting in which Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
's theory of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
is conveniently formulated. For Minkowski space, n = 4 and k = 3 so that
The geometry associated with this pseudo-metric was investigated by Poincaré
Poincaré
Several members of the French Poincaré family have been successful in public and scientific life:* Henri Poincaré , physicist, mathematician and philosopher of science* Lucien Poincaré , physicist, brother of Raymond and cousin of Henri...
who showed its consistency in spite of a total breakdown of the usual properties of Euclidean space. For example a straight line may be perpendicular to itself.
Another pseudo-Euclidean space is the plane z = x + y j consisting of split-complex number
Split-complex number
In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
s, equipped with the quadratic form
The magnitude of a vector x in the space is defined as q(x). In a pseudo-Euclidean space, unlike in a Euclidean space, there exist non-zero vectors with zero magnitude, and also vectors with negative magnitude.
Associated with the quadratic form q is the pseudo-Euclidean inner product
This bilinear form is symmetric, but not positive-definite, so it is not a true inner product.
Whereas Euclidean space has a unit sphere
Unit sphere
In mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...
, pseudo-Euclidean space has the hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
s {x : q(x) = 1 } and {x : q(x) = −1}. Such a hypersurface, called a hyperboloid or unit quasi-sphere, is preserved by the appropriate indefinite orthogonal group.
Every pseudo-Euclidean space has a linear cone given by {x : q(x) = 0 }. When the pseudo-Euclidean space provides a model for spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
, the linear cone is called the light cone
Light cone
A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...
of the origin.