
Pseudo-monotone operator
Encyclopedia
In mathematics
, a pseudo-monotone operator from a reflexive
Banach space
into its continuous dual space is one that is, in some sense, almost as well-behaved
as a monotone operator. Many problems in the calculus of variations
can be expressed using operators that are pseudo-monotone, and pseudo-monotonicity in turn implies the existence of solutions to these problems.
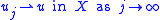
(i.e. uj converges weakly
to u) and
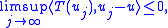
it follows that, for all v ∈ X,
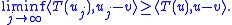
, one can show the following:
Let (X, || ||) be a real
, reflexive Banach space and suppose that T : X → X∗ is continuous
, coercive
and pseudo-monotone. Then, for each continuous linear functional g ∈ X∗, there exists a solution u ∈ X of the equation T(u) = g.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a pseudo-monotone operator from a reflexive
Reflexive space
In functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C...
Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
into its continuous dual space is one that is, in some sense, almost as well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
as a monotone operator. Many problems in the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
can be expressed using operators that are pseudo-monotone, and pseudo-monotonicity in turn implies the existence of solutions to these problems.
Definition
Let (X, || ||) be a reflexive Banach space. A linear map T : X → X∗ from X into its continuous dual space X∗ is said to be pseudo-monotone if T is a bounded linear operator and if whenever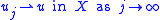
(i.e. uj converges weakly
Weak topology
In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
to u) and
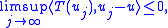
it follows that, for all v ∈ X,
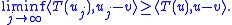
Properties of pseudo-monotone operators
Using a very similar proof to that of the Browder-Minty theoremBrowder-Minty theorem
In mathematics, the Browder–Minty theorem states that a bounded, continuous, coercive and monotone function T from a real, separable reflexive Banach space X into its continuous dual space X∗ is automatically surjective...
, one can show the following:
Let (X, || ||) be a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, reflexive Banach space and suppose that T : X → X∗ is continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, coercive
Coercive function
In mathematics, a coercive function is a function that "grows rapidly" at the extremes of the space on which it is defined. More precisely, a function f : Rn → Rn is called coercive if...
and pseudo-monotone. Then, for each continuous linear functional g ∈ X∗, there exists a solution u ∈ X of the equation T(u) = g.

