Pseudoconvex function
Encyclopedia
In convex analysis
and the calculus of variations
, branches of mathematics
, a pseudoconvex function is a function
that behaves like a convex function
with respect to finding its local minima, but need not actually be convex. Informally, a differentiable function is pseudoconvex if it is increasing in any direction where it has a positive directional derivative
.
open set
X in the finite-dimensional Euclidean space
Rn is said to be pseudoconvex if, for all such that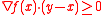
, we have 
. Here ∇ƒ is the gradient
of ƒ, defined by
, but the converse is not true since the function is quasiconvex but not pseudoconvex. Pseudoconvexity is primarily of interest because a point x* is a local minimum of a pseudoconvex function ƒ if and only if it is a stationary point
of ƒ, which is to say that the gradient
of ƒ vanishes at x*: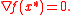
of ƒ by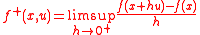
where u is any unit vector. The function is said to be pseudoconvex if it is increasing in any direction where the upper Dini derivative is positive. More precisely, this is characterized in terms of the subdifferential ∂ƒ as follows:
s have pseudolinear objective functions and linear–inequality constraints
: These properties allow fractional–linear problems to be solved by a variant of the simplex algorithm
(of George B. Dantzig).
Convex analysis
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory....
and the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
, branches of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a pseudoconvex function is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that behaves like a convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
with respect to finding its local minima, but need not actually be convex. Informally, a differentiable function is pseudoconvex if it is increasing in any direction where it has a positive directional derivative
Directional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
.
Formal definition
Formally, a real-valued differentiable function ƒ defined on a (nonempty) convexConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
X in the finite-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn is said to be pseudoconvex if, for all such that
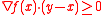, we have . Here ∇ƒ is the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of ƒ, defined by
Properties
Every convex function is pseudoconvex, but the converse is not true. For example, the function is pseudoconvex but not convex. Any pseudoconvex function is quasiconvexQuasiconvex function
In mathematics, a quasiconvex function is a real-valued function defined on an interval or on a convex subset of a real vector space such that the inverse image of any set of the form is a convex set...
, but the converse is not true since the function is quasiconvex but not pseudoconvex. Pseudoconvexity is primarily of interest because a point x* is a local minimum of a pseudoconvex function ƒ if and only if it is a stationary point
Stationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
of ƒ, which is to say that the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of ƒ vanishes at x*:
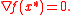
Generalization to nondifferentiable functions
The notion of pseudoconvexity can be generalized to nondifferentiable functions as follows. Given any function we can define the upper Dini derivativeDini derivative
In mathematics and, specifically, real analysis, the Dini derivatives are a class of generalizations of the derivative...
of ƒ by
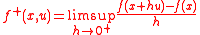
where u is any unit vector. The function is said to be pseudoconvex if it is increasing in any direction where the upper Dini derivative is positive. More precisely, this is characterized in terms of the subdifferential ∂ƒ as follows:
- For all , if there exists an such that
then for all z on the line segment adjoining x and y.
Related notions
A pseudoconcave function is a function whose negative is pseudoconvex. A pseudolinear function is a function that is both pseudoconvex and pseudoconcave. For example, linear–fractional programLinear-fractional programming
In mathematical optimization, linear-fractional programming is a generalization of linear programming . Whereas the objective function in linear programs are linear functions, the objective function in a linear-fractional program is a ratio of two linear functions...
s have pseudolinear objective functions and linear–inequality constraints
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
: These properties allow fractional–linear problems to be solved by a variant of the simplex algorithm
Simplex algorithm
In mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....
(of George B. Dantzig).