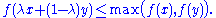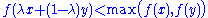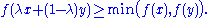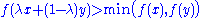In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a quasiconvex function is a real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

-valued function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

 defined on an interval

Interval (mathematics)

In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...

 or on a convex subset

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

 of a real vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

 such that the inverse image of any set of the form is a convex set

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

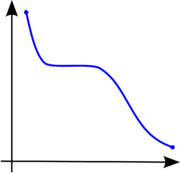
. Informally, after cutting off the top of the function and looking down at the remaining part of the domain, an observer always sees something that is convex.

All convex function

Convex function

In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...

s are also quasiconvex, but not all quasiconvex functions are convex, so quasiconvexity is a generalization of convexity. Quasiconvexity extends the notion of unimodality for functions with a single real argument.

Definition and properties

A function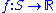 defined on a convex subset S of a real vector space is quasiconvex if for all 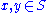and we have

In words, if f is such that it is always true that a point directly between two other points does not give a higher a value of the function than do both of the other points, then f is quasiconvex. Note that the points x and y, and the point directly between them, can be points on a line or more generally points in n-dimensional space.

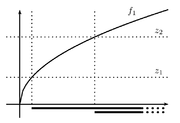
An alternative way (see introduction) of defining a quasi-convex function 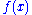is to require that each sub-levelset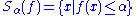

is a convex set.

If furthermore

for all 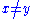and 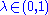, then 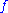is strictly quasiconvex. That is, strict quasiconvexity requires that a point directly between two other points must give a lower value of the function than one of the other points does.

A quasiconcave function is a function whose negative is quasiconvex, and a strictly quasiconcave function is a function whose negative is strictly quasiconvex. Equivalently a function 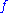is quasiconcave if

and strictly quasiconcave if

A (strictly) quasiconvex function has (strictly) convex lower contour sets, while a (strictly) quasiconcave function has (strictly) convex upper contour sets.

A function that is both quasiconvex and quasiconcave is quasilinear.

Applications

Quasiconvex functions have applications in mathematical analysis

Mathematical analysis

Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...

, in mathematical optimization, and in game theory

Game theory

Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...

 and economics

Economics

Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...

.

Mathematical optimization

In nonlinear optimization

Nonlinear programming

In mathematics, nonlinear programming is the process of solving a system of equalities and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function to be maximized or minimized, where some of the constraints or the objective function are...

, quasiconvex programming studies iterative method

Iterative method

In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...

s that converge to a minimum (if one exists) for quasiconvex functions. Quasiconvex programming is a generalization of convex programming. Quasiconvex programming is used in the solution of "surrogate" dual problem

Dual problem

In constrained optimization, it is often possible to convert the primal problem to a dual form, which is termed a dual problem. Usually dual problem refers to the Lagrangian dual problem but other dual problems are used, for example, the Wolfe dual problem and the Fenchel dual problem...

s, whose biduals provide quasiconvex closures of the primal problem, which therefore provide tighter bounds than do the convex closures provided by Lagrangian dual problems. In theory

Computational Complexity

Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...

, quasiconvex programming and convex programming problems can be solved in reasonable amount of time, where the number of iterations grows like a polynomial in the dimension of the problem (and in the reciprocal of the approximation error tolerated); however, such theoretically "efficient" methods use "divergent-series" stepsize rules, which were first developed for classical subgradient method

Subgradient method

Subgradient methods are iterative methods for solving convex minimization problems. Originally developed by Naum Z. Shor and others in the 1960s and 1970s, subgradient methods are convergent when applied even to a non-differentiable objective function...

s. Classical subgradient methods using divergent-series rules are much slower than modern methods of convex minimization, such as subgradient projection methods, bundle methods of descent, and nonsmooth filter methods.

Economics and partial differential equations: Minimax theorems

In microeconomics

Microeconomics

Microeconomics is a branch of economics that studies the behavior of how the individual modern household and firms make decisions to allocate limited resources. Typically, it applies to markets where goods or services are being bought and sold...

, quasiconcave utility functions imply that consumers have convex preferences

Convex preferences

In economics, convex preferences refer to a property of an individual's ordering of various outcomes which roughly corresponds to the idea that "averages are better than the extremes"...

. Quasiconvex functions are important
also in game theory

Game theory

Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...

, industrial organization

Industrial organization

Industrial organization is the field of economics that builds on the theory of the firm in examining the structure of, and boundaries between, firms and markets....

, and general equilibrium theory, particularly for applications of Sion's minimax theorem

Sion's minimax theorem

In mathematics, and in particular game theory, Sion's minimax theorem is a generalization of John von Neumann's minimax theorem.It states:Let X be a compact convex subset of a linear topological space and Y a convex subset of a linear topological space. If f is a real-valued function on X\times Y...

. Generalizing a minimax theorem of John von Neumann

John von Neumann

John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...

, Sion's theorem is also used in the theory of partial differential equation

Partial differential equation

In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...

s.

Operations preserving quasiconvexity

• non-negative weighted maximum of quasiconvex functions (i.e. with 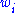non-negative)
• composition with a non-decreasing function (i.e. 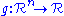quasiconvex, 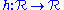non-decreasing, then 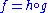is quasiconvex)
• minimization (i.e. 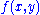quasiconvex, convex set, then 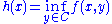is quasiconvex)

Operations not preserving quasiconvexity

• The sum of quasiconvex functions defined on the same domain need not be quasiconvex: In other words, if 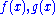are quasiconvex, then 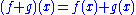need not be quasiconvex.
• The sum of quasiconvex functions defined on different domains (i.e. if 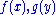are quasiconvex, 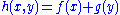) need not be quasiconvex. Such functions are called "additively decomposed" in economics and "separable" in mathematical optimization.

In fact, if the sum of a finite set of (nonconstant) quasiconvex functions is quasiconvex, then all but either zero or one of the functions must be convex; this result holds for separable functions, in particular.

Examples

• Every convex function is quasiconvex.
• A concave function can be quasiconvex function. For example log(x) is concave, and it is quasiconvex.
• Any monotonic function
  Monotonic function
  In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
  
   is both quasiconvex and quasiconcave. More generally, a function which decreases up to a point and increases from that point on is quasiconvex (compare unimodality
  Unimodality
  Unimodality is a term used in several contexts in mathematics. Originally, it relates to possessing a unique mode.- Unimodal probability distribution :...
  
  ).
• The floor function
  Floor function
  In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
  
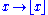    is an example of a quasiconvex function that is neither convex nor continuous.
• If f(x) and g(y) are positive convex decreasing functions, then 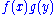is quasiconvex.

See also

• Convex function
  Convex function
  In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
  
  
• Concave function
  Concave function
  In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...
  
  
• Pseudoconvexity in the sense of several complex variables (not generalized convexity)
• Pseudoconvex function
  Pseudoconvex function
  In convex analysis and the calculus of variations, branches of mathematics, a pseudoconvex function is a function that behaves like a convex function with respect to finding its local minima, but need not actually be convex...
  
  
• Invex function
  Invex function
  In vector calculus, an invex function is a differentiable function ƒ from Rn to R for which there exists a vector valued function g such thatfor all x and u....
  
  

External links

• SION, M., "On general minimax theorems", Pacific J. Math. 8 (1958), 171-176.
• Mathematical programming glossary
• Concave and Quasi-Concave Functions - by Charles Wilson, NYU Department of Economics
• Quasiconcavity and quasiconvexity - by Martin J. Osborne, University of Toronto
  University of Toronto
  The University of Toronto is a public research university in Toronto, Ontario, Canada, situated on the grounds that surround Queen's Park. It was founded by royal charter in 1827 as King's College, the first institution of higher learning in Upper Canada...
  
  Department of Economics