Quadruple precision floating-point format
Encyclopedia
In computing
, quadruple precision (also commonly shortened to quad precision) is a binary floating-point computer number format that occupies 16 bytes (128 bits) in computer memory.
In IEEE 754-2008 the 128-bit base-2 format is officially referred to as binary128.
The format is written with an implicit lead bit with value 1 unless the exponent is stored with all zeros. Thus only 112 bits of the significand
appear in the memory format, but the total precision is 113 bits (approximately 34 decimal digits,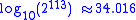
). The bits are laid out as follows:
representation, with the zero offset being 16383; also known as exponent bias in the IEEE 754 standard.
Thus, as defined by the offset binary representation, in order to get the true exponent the offset of 16383 has to be subtracted from the stored exponent.
The stored exponents 0x0000 and 0x7fff are interpreted specially.
The maximum representable value is ≈ 1.1897 × 104932.
,
of the floating-point value. This includes the sign, (biased) exponent, and significand.
3fff 0000 0000 0000 0000 0000 0000 0000 = 1
c000 0000 0000 0000 0000 0000 0000 0000 = -2
7ffe ffff ffff ffff ffff ffff ffff ffff ≈ 1.189731495357231765085759326628007 × 104932 (max quadruple precision)
0000 0000 0000 0000 0000 0000 0000 0000 = 0
8000 0000 0000 0000 0000 0000 0000 0000 = -0
7fff 0000 0000 0000 0000 0000 0000 0000 = infinity
ffff 0000 0000 0000 0000 0000 0000 0000 = -infinity
3ffd 5555 5555 5555 5555 5555 5555 5555 ≈ 1/3
By default, 1/3 rounds down like double precision
, because of the odd number of bits in the significand.
So the bits beyond the rounding point are
.
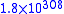for double-double versus 
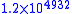for binary128).
In particular, a double-double/quadruple-precision value q in the double-double technique is represented implicitly as a sum q=x+y of two double-precision values x and y, each of which supplies half of qs significand. That is, the pair (x,y) is stored in place of q, and operations on q values (+,−,×,...) are transformed into equivalent (but more complicated) operations on the x and y values. Thus, arithmetic in this technique reduces to a sequence of double-precision operations; since double-precision arithmetic is commonly implemented in hardware, double-double arithmetic is typically substantially faster than more general arbitrary-precision arithmetic
techniques.
libraries to obtain quadruple (or higher) precision, but specialized quadruple-precision implementations may achieve higher performance.
s.
Quadruple precision is specified in Fortran
by the
and by the GNU Fortran compiler
on x86, x86-64
, and Itanium
architectures, for example.)
In the C
/C++
with a few systems and compilers, quadruple precision may be specified by the long double
type, but this is not required by the language (which only requires
(e.g. the GNU C Compiler gcc and the Intel C++ compiler
with a
(as double-double) and SPARC
, or the Sun Studio compilers
on SPARC. Even if
CPUs, and some versions of Intel's C/C++ compiler for x86 and x86-64 supply a nonstandard quadruple-precision type called
V8 and V9 architectures (e.g. there are 16 quad-precision registers %q0, %q4, ...), but no SPARC CPU implements quad-precision operations in hardware.
As at 2005, there are no native 128-bits FPUs.
Non-IEEE extended-precision (128 bit of storage, 1 sign bit, 7 exponent bit, 112 fraction bit, 8 bits unused) was added to the System/370 series and was available on some S/360 models (S/360-85, -195, and others by special request or simulated by OS software).
Computing
Computing is usually defined as the activity of using and improving computer hardware and software. It is the computer-specific part of information technology...
, quadruple precision (also commonly shortened to quad precision) is a binary floating-point computer number format that occupies 16 bytes (128 bits) in computer memory.
In IEEE 754-2008 the 128-bit base-2 format is officially referred to as binary128.
IEEE 754 quadruple-precision binary floating-point format: binary128
The IEEE 754 standard specifies a binary128 as having:- Sign bitSign bitIn computer science, the sign bit is a bit in a computer numbering format that indicates the sign of a number. In IEEE format, the sign bit is the leftmost bit...
: 1 - Exponent width: 15
- SignificandSignificandThe significand is part of a floating-point number, consisting of its significant digits. Depending on the interpretation of the exponent, the significand may represent an integer or a fraction.-Examples:...
precisionPrecision (arithmetic)The precision of a value describes the number of digits that are used to express that value. In a scientific setting this would be the total number of digits or, less commonly, the number of fractional digits or decimal places...
: 113 (112 explicitly stored)
The format is written with an implicit lead bit with value 1 unless the exponent is stored with all zeros. Thus only 112 bits of the significand
Significand
The significand is part of a floating-point number, consisting of its significant digits. Depending on the interpretation of the exponent, the significand may represent an integer or a fraction.-Examples:...
appear in the memory format, but the total precision is 113 bits (approximately 34 decimal digits,
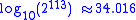). The bits are laid out as follows:Exponent encoding
The quadruple-precision binary floating-point exponent is encoded using an offset binaryOffset binary
Offset binary, also referred to as excess-K, is a digital coding scheme where all-zero corresponds to the minimal negative value and all-one to the maximal positive value. There is no standard for offset binary, but most often the offset K for an n-bit binary word is K=2^...
representation, with the zero offset being 16383; also known as exponent bias in the IEEE 754 standard.
- Emin = 0x0001−0x3fff = −16382
- Emax = 0x7ffe−0x3fff = 16383
- Exponent biasExponent biasIn IEEE 754 floating point numbers, the exponent is biased in the engineering sense of the word – the value stored is offset from the actual value by the exponent bias....
= 0x3fff = 16383
Thus, as defined by the offset binary representation, in order to get the true exponent the offset of 16383 has to be subtracted from the stored exponent.
The stored exponents 0x0000 and 0x7fff are interpreted specially.
| Exponent | Significand zero | Significand non-zero | Equation |
|---|---|---|---|
| 0x0000 | 0 0 (number) 0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems... , −0 |
subnormal numbers |  |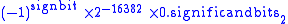
| 0x0001, ..., 0x7ffe | normalized value |  |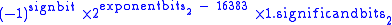
|
| 0x7fff | ±infinity Infinity Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity... |
NaN NaN In computing, NaN is a value of the numeric data type representing an undefined or unrepresentable value, especially in floating-point calculations... (quiet, signalling) |
|
The maximum representable value is ≈ 1.1897 × 104932.
Quadruple-precision examples
These examples are given in bit representation, in hexadecimalHexadecimal
In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen...
,
of the floating-point value. This includes the sign, (biased) exponent, and significand.
3fff 0000 0000 0000 0000 0000 0000 0000 = 1
c000 0000 0000 0000 0000 0000 0000 0000 = -2
7ffe ffff ffff ffff ffff ffff ffff ffff ≈ 1.189731495357231765085759326628007 × 104932 (max quadruple precision)
0000 0000 0000 0000 0000 0000 0000 0000 = 0
8000 0000 0000 0000 0000 0000 0000 0000 = -0
7fff 0000 0000 0000 0000 0000 0000 0000 = infinity
ffff 0000 0000 0000 0000 0000 0000 0000 = -infinity
3ffd 5555 5555 5555 5555 5555 5555 5555 ≈ 1/3
By default, 1/3 rounds down like double precision
Double precision
In computing, double precision is a computer number format that occupies two adjacent storage locations in computer memory. A double-precision number, sometimes simply called a double, may be defined to be an integer, fixed point, or floating point .Modern computers with 32-bit storage locations...
, because of the odd number of bits in the significand.
So the bits beyond the rounding point are
0101... which is less than 1/2 of a unit in the last placeUnit in the Last Place
In computer science and numerical analysis, unit in the last place or unit of least precision is the spacing between floating-point numbers, i.e., the value the least significant bit represents if it is 1...
.
Double-double arithmetic
A common software technique to implement nearly quadruple precision using pairs of double-precision values is sometimes called double-double arithmetic. Using pairs of IEEE double-precision values with 53-bit significands, double-double arithmetic can represent operations with at least a 2×53=106-bit significand (and possibly 107 bits via clever use of the sign bit), only slightly less precise than the 113-bit significand of IEEE binary128 quadruple precision. The range of a double-double remains essentially the same as the double-precision format because the exponent has still 11 bits, significantly lower than the 15-bit exponent of IEEE quadruple precision (a range of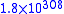 for double-double versus 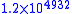for binary128).In particular, a double-double/quadruple-precision value q in the double-double technique is represented implicitly as a sum q=x+y of two double-precision values x and y, each of which supplies half of qs significand. That is, the pair (x,y) is stored in place of q, and operations on q values (+,−,×,...) are transformed into equivalent (but more complicated) operations on the x and y values. Thus, arithmetic in this technique reduces to a sequence of double-precision operations; since double-precision arithmetic is commonly implemented in hardware, double-double arithmetic is typically substantially faster than more general arbitrary-precision arithmetic
Arbitrary-precision arithmetic
In computer science, arbitrary-precision arithmetic indicates that calculations are performed on numbers whose digits of precision are limited only by the available memory of the host system. This contrasts with the faster fixed-precision arithmetic found in most ALU hardware, which typically...
techniques.
Implementations
Quadruple precision is almost always implemented in software by a variety of techniques (such as the double-double technique above, although that technique does not implement IEEE quadruple precision), since direct hardware support for quadruple precision is extremely rare. One can use general arbitrary-precision arithmeticArbitrary-precision arithmetic
In computer science, arbitrary-precision arithmetic indicates that calculations are performed on numbers whose digits of precision are limited only by the available memory of the host system. This contrasts with the faster fixed-precision arithmetic found in most ALU hardware, which typically...
libraries to obtain quadruple (or higher) precision, but specialized quadruple-precision implementations may achieve higher performance.
Computer-language support
A separate question is the extent to which quadruple-precision types are directly incorporated into computer programming languageProgramming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s.
Quadruple precision is specified in Fortran
Fortran
Fortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
by the
REAL*16 or REAL(KIND=16) type, although this type is not supported by all compilers. (Quadruple-precision REAL*16 is supported by the Intel Fortran CompilerIntel Fortran Compiler
Intel Fortran Compiler, also known as IFORT, is a Fortran compiler developed by Intel. It generates code for IA-32, Intel 64 processors. Compilers are available for Linux, Microsoft Windows and Mac OS X. On Windows, it is known as Intel Visual Fortran...
and by the GNU Fortran compiler
GFortran
gfortran is the name of the GNU Fortran compiler, which is part of the GNU Compiler Collection . gfortran has replaced the g77 compiler, which stopped development before GCC version 4.0. It includes support for the Fortran 95 language and is compatible with most language extensions supported by...
on x86, x86-64
X86-64
x86-64 is an extension of the x86 instruction set. It supports vastly larger virtual and physical address spaces than are possible on x86, thereby allowing programmers to conveniently work with much larger data sets. x86-64 also provides 64-bit general purpose registers and numerous other...
, and Itanium
Itanium
Itanium is a family of 64-bit Intel microprocessors that implement the Intel Itanium architecture . Intel markets the processors for enterprise servers and high-performance computing systems...
architectures, for example.)
In the C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
/C++
C++
C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
with a few systems and compilers, quadruple precision may be specified by the long double
Long double
In C and related programming languages, long double refers to a floating point data type that is often more precise than double precision. As with C's other floating point types, it may not necessarily map to an IEEE format.-History:...
type, but this is not required by the language (which only requires
long double to be at least as precise as double), nor is it common. On x86 and x86-64, the most common C/C++ compilers implement long double as either 80-bit extended precisionExtended precision
The term extended precision refers to storage formats for floating point numbers not falling into the regular sequence of single, double, and quadruple precision formats...
(e.g. the GNU C Compiler gcc and the Intel C++ compiler
Intel C++ Compiler
Intel C++ Compiler is a group of C and C++ compilers from Intel Corporation available for GNU/Linux, Mac OS X, and Microsoft Windows....
with a
/Qlong‑double switch) or simply as being synonymous with double precision (e.g. Microsoft Visual C++), rather than as quadruple precision. On a few other architectures, some C/C++ compilers implement long double as quadruple precision, e.g. gcc on PowerPCPowerPC
PowerPC is a RISC architecture created by the 1991 Apple–IBM–Motorola alliance, known as AIM...
(as double-double) and SPARC
SPARC
SPARC is a RISC instruction set architecture developed by Sun Microsystems and introduced in mid-1987....
, or the Sun Studio compilers
Sun Studio (software)
The Oracle Solaris Studio compiler suite is Oracle's flagship software development product for Solaris and Linux. It was formerly known as Sun Studio...
on SPARC. Even if
long double is not quadruple precision, however, some C/C++ compilers provide a nonstandard quadruple-precision type as an extension. For example, gcc provides a quadruple-precision type called __float128 for x86, x86-64 and ItaniumItanium
Itanium is a family of 64-bit Intel microprocessors that implement the Intel Itanium architecture . Intel markets the processors for enterprise servers and high-performance computing systems...
CPUs, and some versions of Intel's C/C++ compiler for x86 and x86-64 supply a nonstandard quadruple-precision type called
_Quad.Hardware support
Native support of 128-bit floats is defined in SPARCSPARC
SPARC is a RISC instruction set architecture developed by Sun Microsystems and introduced in mid-1987....
V8 and V9 architectures (e.g. there are 16 quad-precision registers %q0, %q4, ...), but no SPARC CPU implements quad-precision operations in hardware.
As at 2005, there are no native 128-bits FPUs.
Non-IEEE extended-precision (128 bit of storage, 1 sign bit, 7 exponent bit, 112 fraction bit, 8 bits unused) was added to the System/370 series and was available on some S/360 models (S/360-85, -195, and others by special request or simulated by OS software).
See also
- IEEE Standard for Floating-Point Arithmetic (IEEE 754)
- Extended precisionExtended precisionThe term extended precision refers to storage formats for floating point numbers not falling into the regular sequence of single, double, and quadruple precision formats...
(80-bit) - ISO/IEC 10967ISO/IEC 10967ISO/IEC 10967, Language independent arithmetic , is a series ofstandards on computer arithmetic. It is compatible with IEC 60559, and indeed much of thespecifications in parts 2 and 3 are for IEEE 754 special values...
, Language Independent Arithmetic - Primitive data type
- long doubleLong doubleIn C and related programming languages, long double refers to a floating point data type that is often more precise than double precision. As with C's other floating point types, it may not necessarily map to an IEEE format.-History:...
External links
- High-Precision Software Directory
- QPFloat, a free softwareFree softwareFree software, software libre or libre software is software that can be used, studied, and modified without restriction, and which can be copied and redistributed in modified or unmodified form either without restriction, or with restrictions that only ensure that further recipients can also do...
(GPL) software library for quadruple-precision arithmetic - HPAlib, a free software (LGPL) software library for quad-precision arithmetic
- libquadmath, the GCCGNU Compiler CollectionThe GNU Compiler Collection is a compiler system produced by the GNU Project supporting various programming languages. GCC is a key component of the GNU toolchain...
quad-precision math library