Quantitative models of the action potential
Encyclopedia
In neurophysiology
, several mathematical models of the action potential
have been developed, which fall into two basic types. The first type seeks to model the experimental data quantitatively, i.e., to reproduce the measurements of current and voltage exactly. The renowned Hodgkin-Huxley model
of the axon from the Loligo
squid exemplifies such models.
Although qualitatively correct, the H-H model does not describe every type of excitable membrane accurately, since it considers only two ions (sodium and potassium), each with only one type of voltage-sensitive channel. However, other ions such as calcium
may be important and there is a great diversity of channels for all ions. As an example, the cardiac action potential
illustrates how differently shaped action potentials can be generated on membranes with voltage-sensitive calcium channels and different types of sodium/potassium channels. The second type of mathematical model is a simplification of the first type; the goal is not to reproduce the experimental data, but to understand qualitatively the role of action potentials in neural circuits. For such a purpose, detailed physiological models may be unnecessarily complicated and may obscure the "forest for the trees". The Fitzhugh-Nagumo model is typical of this class, which is often studied for its entrainment behavior
. Entrainment is commonly observed
in nature, for example in the synchronized lighting of fireflies
, which is coordinated by a burst of action potentials; entrainment can also be observed in individual neurons. Both types of models may be used to understand the behavior of small biological neural network
s, such as the central pattern generator
s responsible for some automatic reflex actions. Such networks can generate a complex temporal pattern of action potentials that is used to coordinate muscular contractions, such as those involved in breathing or fast swimming to escape a predator.
and Andrew Huxley
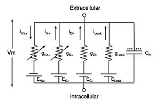
developed a set of equations to fit their experimental voltage-clamp data on the axonal membrane. The model assumes that the membrane capacitance C is constant; thus, the transmembrane voltage V changes with the total transmembrane current Itot according to the equation
where INa, IK, and IL are currents conveyed through the local sodium channels, potassium channels, and "leakage" channels (a catch-all), respectively. The initial term Iext represents the current arriving from external sources, such as excitatory postsynaptic potential
s from the dendrites or a scientist's electrode.
The model further assumes that a given ion channel is either fully open or closed; if closed, its conductance
is zero, whereas if open, its conductance is some constant value g. Hence, the net current through an ion channel depends on two variables: the probability popen of the channel being open, and the difference in voltage from that ion's equilibrium voltage, V − Veq. For example, the current through the potassium channel may be written as
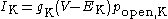
which is equivalent to Ohm's law
. By definition, no net current flows (IK = 0) when the transmembrane voltage equals the equilibrium voltage of that ion (when V = EK).
To fit their data accurately, Hodgkin and Huxley assumed that each type of ion channel had multiple "gates", so that the channel was open only if all the gates were open and closed otherwise. They also assumed that the probability of a gate being open was independent of the other gates being open; this assumption was later validated for the inactivation gate. Hodgkin and Huxley modeled the voltage-sensitive potassium channel as having four gates; letting pn denote the probability of a single such gate being open, the probability of the whole channel being open is the product of four such probabilities, i.e., popen, K = n4. Similarly, the probability of the voltage-sensitive sodium channel was modeled to have three similar gates of probability m and a fourth gate, associated with inactivation, of probability h; thus, popen, Na = m3h. The probabilities for each gate are assumed to obey first-order kinetics
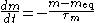
where both the equilibrium value meq and the relaxation time constant τm depend on the instantaneous voltage V across the membrane. If V changes on a time-scale more slowly than τm, the m probability will always roughly equal its equilibrium value meq; however, if V changes more quickly, then m will lag behind meq. By fitting their voltage-clamp data, Hodgkin and Huxley were able to model how these equilibrium values and time constants varied with temperature and transmembrane voltage. The formulae are complex and depend exponentially on the voltage and temperature. For example, the time constant for sodium-channel activation probability h varies as 3(θ−6.3)/10 with the Celsius temperature θ, and with voltage V as
In summary, the Hodgkin-Huxley equations are complex, non-linear ordinary differential equation
s in four independent variable
s: the transmembrane voltage V, and the probabilities m, h and n. No general solution of these equations has been discovered. A less ambitious but generally applicable method for studying such non-linear dynamical systems is to consider their behavior in the vicinity of a fixed point
. This analysis shows that the Hodgkin-Huxley system undergoes a transition from stable quiescence to bursting
oscillations as the stimulating current Iext is gradually increased; remarkably, the axon becomes stably quiescent again as the stimulating current is increased further still. A more general study of the types of qualitative behavior of axons predicted by the Hodgkin-Huxley equations has also been carried out.
Because of the complexity of the Hodgkin-Huxley equations, various simplifications have been developed that exhibit qualitatively similar behavior. The Fitzhugh-Nagumo model is a typical example of such a simplified system. Based on the tunnel diode
, the FHN model has only two independent variables, but exhibits a similar stability behavior to the full Hodgkin-Huxley equations. The equations are
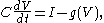
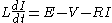
where g(V) is a function of the voltage V that has a region of negative slope in the middle, flanked by one maximum and one minimum (Figure FHN). A much-studied simple case of the Fitzhugh-Nagumo model is the Bonhoeffer-van der Pol nerve model, which is described by the equations
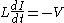
where the coefficient ε is assumed to be small. These equations can be combined into a second-order differential equation
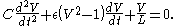
This van der Pol equation has stimulated much research in the mathematics of nonlinear dynamical system
s. Op-amp
circuits that realize the FHN and van der Pol models of the action potential have been developed by Keener.
A hybrid of the Hodgkin-Huxley and FitzHugh-Nagumo models was developed by Morris and Lecar in 1981, and applied to the muscle
fiber of barnacle
s. True to the barnacle's physiology, the Morris-Lecar model replaces the voltage-gated sodium current of the Hodgkin-Huxley model with a voltage-dependent calcium current. There is no inactivation (no h variable) and the calcium current equilibrates instantaneously, so that again, there are only two time-dependent variables: the transmembrane voltage V and the potassium gate probability n. The bursting, entrainment and other mathematical properties of this model have been studied in detail.
The simplest models of the action potential are the "flush and fill" models (also called "integrate-and-fire" models), in which the input signal is summed (the "fill" phase) until it reaches a threshold, firing a pulse and resetting the summation to zero (the "flush" phase). All of these models are capable of exhibiting entrainment
, which is commonly observed
in nervous systems.
; in such solutions, the current follows the electric
field line
s, according to the continuum form of Ohm's Law
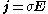
where j and E are vectors representing the current density
and electric field
, respectively, and where σ is the conductivity. Thus, j can be found from E, which in turn may be found using Maxwell's equations
. Maxwell's equations can be reduced to a relatively simple problem of electrostatics
, since the ionic concentrations change too slowly (compared to the speed of light
) for magnetic effects
to be important. The electric potential
φ(x) at any extracellular point x can be solved using Green's identities
where the integration is over the complete surface of the membrane;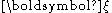
is a position on the membrane, σinside and φinside are the conductivity and potential just within the membrane, and σoutside and φoutside the corresponding values just outside the membrane. Thus, given these σ and φ values on the membrane, the extracellular potential φ(x) can be calculated for any position x; in turn, the electric field E and current density j can be calculated from this potential field.
Neurophysiology
Neurophysiology is a part of physiology. Neurophysiology is the study of nervous system function...
, several mathematical models of the action potential
Action potential
In physiology, an action potential is a short-lasting event in which the electrical membrane potential of a cell rapidly rises and falls, following a consistent trajectory. Action potentials occur in several types of animal cells, called excitable cells, which include neurons, muscle cells, and...
have been developed, which fall into two basic types. The first type seeks to model the experimental data quantitatively, i.e., to reproduce the measurements of current and voltage exactly. The renowned Hodgkin-Huxley model
Hodgkin-Huxley model
The Hodgkin–Huxley model is a mathematical model that describes how action potentials in neurons are initiated and propagated....
of the axon from the Loligo
Loligo
Loligo is a genus of squids and one of the most representative and widely distributed groups of myopsid squids.The genus was first described by Jean Baptiste Lamarck in 1798. However, the name had been used earlier than Lamarck and might even have been used by Pliny...
squid exemplifies such models.
Although qualitatively correct, the H-H model does not describe every type of excitable membrane accurately, since it considers only two ions (sodium and potassium), each with only one type of voltage-sensitive channel. However, other ions such as calcium
Calcium
Calcium is the chemical element with the symbol Ca and atomic number 20. It has an atomic mass of 40.078 amu. Calcium is a soft gray alkaline earth metal, and is the fifth-most-abundant element by mass in the Earth's crust...
may be important and there is a great diversity of channels for all ions. As an example, the cardiac action potential
Cardiac action potential
In electrocardiography, the cardiac action potential is a specialized action potential in the heart, necessary for the electrical conduction system of the heart....
illustrates how differently shaped action potentials can be generated on membranes with voltage-sensitive calcium channels and different types of sodium/potassium channels. The second type of mathematical model is a simplification of the first type; the goal is not to reproduce the experimental data, but to understand qualitatively the role of action potentials in neural circuits. For such a purpose, detailed physiological models may be unnecessarily complicated and may obscure the "forest for the trees". The Fitzhugh-Nagumo model is typical of this class, which is often studied for its entrainment behavior
Entrainment (physics)
Entrainment has been used to refer to the process of mode locking of coupled driven oscillators, which is the process whereby two interacting oscillating systems, which have different periods when they function independently, assume a common period...
. Entrainment is commonly observed
Entrainment (biomusicology)
Entrainment in the biomusicological sense refers to the synchronization of organisms to an external rhythm, usually produced by other organisms with whom they interact socially...
in nature, for example in the synchronized lighting of fireflies
Firefly
Lampyridae is a family of insects in the beetle order Coleoptera. They are winged beetles, and commonly called fireflies or lightning bugs for their conspicuous crepuscular use of bioluminescence to attract mates or prey. Fireflies produce a "cold light", with no infrared or ultraviolet frequencies...
, which is coordinated by a burst of action potentials; entrainment can also be observed in individual neurons. Both types of models may be used to understand the behavior of small biological neural network
Biological neural network
In neuroscience, a biological neural network describes a population of physically interconnected neurons or a group of disparate neurons whose inputs or signalling targets define a recognizable circuit. Communication between neurons often involves an electrochemical process...
s, such as the central pattern generator
Central pattern generator
Central pattern generators are neural networks that produce rhythmic patterned outputs without sensory feedback. CPGs have been shown to produce rhythmic outputs resembling normal "rhythmic motor pattern production" even in isolation from motor and sensory feedback from limbs and other muscle...
s responsible for some automatic reflex actions. Such networks can generate a complex temporal pattern of action potentials that is used to coordinate muscular contractions, such as those involved in breathing or fast swimming to escape a predator.
Hodgkin-Huxley model
In 1952 Alan Lloyd HodgkinAlan Lloyd Hodgkin
Sir Alan Lloyd Hodgkin, OM, KBE, PRS was a British physiologist and biophysicist, who shared the 1963 Nobel Prize in Physiology or Medicine with Andrew Huxley and John Eccles....
and Andrew Huxley
Andrew Huxley
Sir Andrew Fielding Huxley, OM, FRS is an English physiologist and biophysicist, who won the 1963 Nobel Prize in Physiology or Medicine for his experimental and mathematical work with Sir Alan Lloyd Hodgkin on the basis of nerve action potentials, the electrical impulses that enable the activity...
developed a set of equations to fit their experimental voltage-clamp data on the axonal membrane. The model assumes that the membrane capacitance C is constant; thus, the transmembrane voltage V changes with the total transmembrane current Itot according to the equation
where INa, IK, and IL are currents conveyed through the local sodium channels, potassium channels, and "leakage" channels (a catch-all), respectively. The initial term Iext represents the current arriving from external sources, such as excitatory postsynaptic potential
Excitatory postsynaptic potential
In neuroscience, an excitatory postsynaptic potential is a temporary depolarization of postsynaptic membrane potential caused by the flow of positively charged ions into the postsynaptic cell as a result of opening of ligand-sensitive channels...
s from the dendrites or a scientist's electrode.
The model further assumes that a given ion channel is either fully open or closed; if closed, its conductance
Conductance
Conductance may refer to:* Electrical conductance, the ability for electricity to flow a certain path* Fluid conductance, the ability for fluid to transmit through materials* Thermal conductivity, the ability for temperatures to transmit through materials...
is zero, whereas if open, its conductance is some constant value g. Hence, the net current through an ion channel depends on two variables: the probability popen of the channel being open, and the difference in voltage from that ion's equilibrium voltage, V − Veq. For example, the current through the potassium channel may be written as
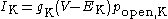
which is equivalent to Ohm's law
Ohm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points...
. By definition, no net current flows (IK = 0) when the transmembrane voltage equals the equilibrium voltage of that ion (when V = EK).
To fit their data accurately, Hodgkin and Huxley assumed that each type of ion channel had multiple "gates", so that the channel was open only if all the gates were open and closed otherwise. They also assumed that the probability of a gate being open was independent of the other gates being open; this assumption was later validated for the inactivation gate. Hodgkin and Huxley modeled the voltage-sensitive potassium channel as having four gates; letting pn denote the probability of a single such gate being open, the probability of the whole channel being open is the product of four such probabilities, i.e., popen, K = n4. Similarly, the probability of the voltage-sensitive sodium channel was modeled to have three similar gates of probability m and a fourth gate, associated with inactivation, of probability h; thus, popen, Na = m3h. The probabilities for each gate are assumed to obey first-order kinetics
Rate equation
The rate law or rate equation for a chemical reaction is an equation that links the reaction rate with concentrations or pressures of reactants and constant parameters . To determine the rate equation for a particular system one combines the reaction rate with a mass balance for the system...
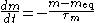
where both the equilibrium value meq and the relaxation time constant τm depend on the instantaneous voltage V across the membrane. If V changes on a time-scale more slowly than τm, the m probability will always roughly equal its equilibrium value meq; however, if V changes more quickly, then m will lag behind meq. By fitting their voltage-clamp data, Hodgkin and Huxley were able to model how these equilibrium values and time constants varied with temperature and transmembrane voltage. The formulae are complex and depend exponentially on the voltage and temperature. For example, the time constant for sodium-channel activation probability h varies as 3(θ−6.3)/10 with the Celsius temperature θ, and with voltage V as
In summary, the Hodgkin-Huxley equations are complex, non-linear ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s in four independent variable
Independent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
s: the transmembrane voltage V, and the probabilities m, h and n. No general solution of these equations has been discovered. A less ambitious but generally applicable method for studying such non-linear dynamical systems is to consider their behavior in the vicinity of a fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
. This analysis shows that the Hodgkin-Huxley system undergoes a transition from stable quiescence to bursting
Bursting
Bursting is an extremely diverse general phenomenon of the activation patterns of neurons in the central nervous system and spinal cord where periods of rapid spiking are followed by quiescent, silent, periods. Bursting is thought to be important in the operation of robust central pattern...
oscillations as the stimulating current Iext is gradually increased; remarkably, the axon becomes stably quiescent again as the stimulating current is increased further still. A more general study of the types of qualitative behavior of axons predicted by the Hodgkin-Huxley equations has also been carried out.
Fitzhugh-Nagumo model
Tunnel diode
A tunnel diode or Esaki diode is a type of semiconductor diode which is capable of very fast operation, well into the microwave frequency region, by using quantum mechanical effects....
, the FHN model has only two independent variables, but exhibits a similar stability behavior to the full Hodgkin-Huxley equations. The equations are
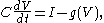
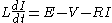
where g(V) is a function of the voltage V that has a region of negative slope in the middle, flanked by one maximum and one minimum (Figure FHN). A much-studied simple case of the Fitzhugh-Nagumo model is the Bonhoeffer-van der Pol nerve model, which is described by the equations
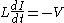
where the coefficient ε is assumed to be small. These equations can be combined into a second-order differential equation
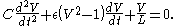
This van der Pol equation has stimulated much research in the mathematics of nonlinear dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s. Op-amp
Operational amplifier
An operational amplifier is a DC-coupled high-gain electronic voltage amplifier with a differential input and, usually, a single-ended output...
circuits that realize the FHN and van der Pol models of the action potential have been developed by Keener.
A hybrid of the Hodgkin-Huxley and FitzHugh-Nagumo models was developed by Morris and Lecar in 1981, and applied to the muscle
Muscle
Muscle is a contractile tissue of animals and is derived from the mesodermal layer of embryonic germ cells. Muscle cells contain contractile filaments that move past each other and change the size of the cell. They are classified as skeletal, cardiac, or smooth muscles. Their function is to...
fiber of barnacle
Barnacle
A barnacle is a type of arthropod belonging to infraclass Cirripedia in the subphylum Crustacea, and is hence related to crabs and lobsters. Barnacles are exclusively marine, and tend to live in shallow and tidal waters, typically in erosive settings. They are sessile suspension feeders, and have...
s. True to the barnacle's physiology, the Morris-Lecar model replaces the voltage-gated sodium current of the Hodgkin-Huxley model with a voltage-dependent calcium current. There is no inactivation (no h variable) and the calcium current equilibrates instantaneously, so that again, there are only two time-dependent variables: the transmembrane voltage V and the potassium gate probability n. The bursting, entrainment and other mathematical properties of this model have been studied in detail.
The simplest models of the action potential are the "flush and fill" models (also called "integrate-and-fire" models), in which the input signal is summed (the "fill" phase) until it reaches a threshold, firing a pulse and resetting the summation to zero (the "flush" phase). All of these models are capable of exhibiting entrainment
Entrainment (physics)
Entrainment has been used to refer to the process of mode locking of coupled driven oscillators, which is the process whereby two interacting oscillating systems, which have different periods when they function independently, assume a common period...
, which is commonly observed
Entrainment (biomusicology)
Entrainment in the biomusicological sense refers to the synchronization of organisms to an external rhythm, usually produced by other organisms with whom they interact socially...
in nervous systems.
Extracellular potentials and currents
Whereas the above models simulate the transmembrane voltage and current at a single patch of membrane, other mathematical models pertain to the voltages and currents in the ionic solution surrounding the neuron. Such models are helpful in interpreting data from extracellular electrodes, which were common prior to the invention of the glass pipette electrode that allowed intracellular recording. The extracellular medium may be modeled as a normal isotropic ionic solutionElectrolyte
In chemistry, an electrolyte is any substance containing free ions that make the substance electrically conductive. The most typical electrolyte is an ionic solution, but molten electrolytes and solid electrolytes are also possible....
; in such solutions, the current follows the electric
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
field line
Field line
A field line is a locus that is defined by a vector field and a starting location within the field. Field lines are useful for visualizing vector fields, which are otherwise hard to depict...
s, according to the continuum form of Ohm's Law
Ohm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points...
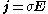
where j and E are vectors representing the current density
Current density
Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
and electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
, respectively, and where σ is the conductivity. Thus, j can be found from E, which in turn may be found using Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
. Maxwell's equations can be reduced to a relatively simple problem of electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
, since the ionic concentrations change too slowly (compared to the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
) for magnetic effects
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
to be important. The electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
φ(x) at any extracellular point x can be solved using Green's identities
Green's identities
In mathematics, Green's identities are a set of three identities in vector calculus. They are named after the mathematician George Green, who discovered Green's theorem.-Green's first identity:...
where the integration is over the complete surface of the membrane;
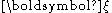is a position on the membrane, σinside and φinside are the conductivity and potential just within the membrane, and σoutside and φoutside the corresponding values just outside the membrane. Thus, given these σ and φ values on the membrane, the extracellular potential φ(x) can be calculated for any position x; in turn, the electric field E and current density j can be calculated from this potential field.See also
- Biological neuron models
- GHK current equationGHK current equationThe Goldman–Hodgkin–Katz flux equation describes the ionic flux carried by an ionic species across a cell membrane as a function of the transmembrane potential and the concentrations of the ion inside and outside of the cell...
- Saltatory conductionSaltatory conductionSaltatory conduction is the propagation of action potentials along myelinated axons from one node of Ranvier to the next node, increasing the conduction velocity of action potentials without needing to increase the diameter of an axon.-Mechanism:Because the cytoplasm of the axon is electrically...
- BioelectronicsBioelectronicsBioelectronics is a recently coined term for a field of research that works to establish a synergy between electronics and biology. One of the main forums for information about the field is the Elsevier journal Biosensors and Bioelectronics, published since 1990...
- Cable theoryCable theoryClassical cable theory uses mathematical models to calculate the flow of electric current along passive neuronal fibers particularly dendrites that receive synaptic inputs at different sites and times...