Quasi-phase-matching
Encyclopedia
Quasi-phase-matching is a technique in nonlinear optics
which allows a positive net flow of energy from the pump frequency to the signal and idler frequencies by creating a periodic structure in the nonlinear medium. Momentum is conserved, as is necessary for phase-matching, through an additional momentum contribution corresponding to the wavevector of the periodic structure. Consequently, in principle any three-wave mixing process that satisfies energy conservation can be phase-matched. For example, all the optical frequencies involved can be collinear, can have the same polarization, and travel through the medium in arbitrary directions. This allows one to use the largest nonlinear coefficient of the material in the nonlinear interaction.
Quasi-phase-matching ensures that there is positive energy flow from the pump frequency to signal and idler frequencies even though all the frequencies involved are not phase locked with each other. Energy will always flow from pump to signal as long the phase between the two optical waves is less than 180 degrees. Beyond 180 degrees, energy flows back from the signal to the pump frequencies. The coherence length
is the length of the medium in which the phase of pump and the sum of idler and signal frequencies are 180 degrees from each other. At each coherence length the crystal axes are flipped which allows the energy to continue to positively flow from the pump to the signal and idler frequencies.
The most commonly used technique for creating quasi-phase-matched crystals is periodic poling
.
polarization equation can be expressed by
Where
is the nonlinear susceptibility coefficient in which the sign of the coefficient is flipped when the crystal axis is flipped. Where 
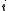represents the imaginary unit
.
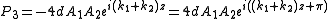
where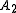
is the generated frequency amplitude and 
is the pump frequency amplitude and 
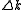is the phase mismatch between the two optical waves. The 
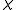refers to the nonlinear susceptibility of the crystal.
In the case of a periodically poled crystal the optic axis is flipped by 180 degrees in every other domain, which changes the sign of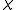
. For the 
domain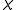 
can be expressed as
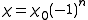
where
is the index of the poled domain. The total signal amplitude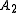 
can be expressed as a sum
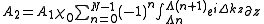
which integrates to
and reduces to
The summation yields
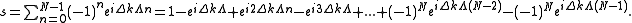
Multiply above equation both sides by a factor of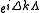
Adding both equation leads to the relation
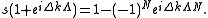
Solving for
gives
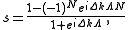
which leads to
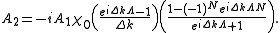
The total intensity can be expressed by
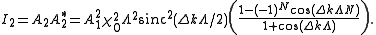
For the case of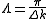
the right part of the above equation is undefined so the limit needs to be taken when 
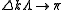by invoking L'Hôpital's rule
.
Which leads to the signal intensity
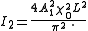
In order to allow different domain widths, ie.
, for 
, the above equation becomes
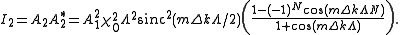
With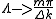
the intensity becomes
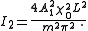
This allows quasi-phase-matching to exist at different domain widths
.
From this equation it is apparent, however, that as the quasi-phase match order
increases, the efficiency decreases by 
. For example for 3rd order quasi-phase matching only a third of the crystal is effectively used for the generation of signal frequency, as a consequence the amplitude of the signal wavelength only third of the amount of amplitude for same length crystal for 1st order quasi-phase match.
and using wavevector relations. In the case of DFG this relationship holds true
where 
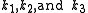are the pump, signal, and idler wavevectors and 
. By calculating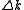 
for the different frequencies the domain width can be calculated from the relationship 
.
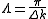Nonlinear optics
Nonlinear optics is the branch of optics that describes the behavior of light in nonlinear media, that is, media in which the dielectric polarization P responds nonlinearly to the electric field E of the light...
which allows a positive net flow of energy from the pump frequency to the signal and idler frequencies by creating a periodic structure in the nonlinear medium. Momentum is conserved, as is necessary for phase-matching, through an additional momentum contribution corresponding to the wavevector of the periodic structure. Consequently, in principle any three-wave mixing process that satisfies energy conservation can be phase-matched. For example, all the optical frequencies involved can be collinear, can have the same polarization, and travel through the medium in arbitrary directions. This allows one to use the largest nonlinear coefficient of the material in the nonlinear interaction.
Quasi-phase-matching ensures that there is positive energy flow from the pump frequency to signal and idler frequencies even though all the frequencies involved are not phase locked with each other. Energy will always flow from pump to signal as long the phase between the two optical waves is less than 180 degrees. Beyond 180 degrees, energy flows back from the signal to the pump frequencies. The coherence length
Coherence length
In physics, coherence length is the propagation distance from a coherent source to a point where an electromagnetic wave maintains a specified degree of coherence. The significance is that interference will be strong within a coherence length of the source, but not beyond it...
is the length of the medium in which the phase of pump and the sum of idler and signal frequencies are 180 degrees from each other. At each coherence length the crystal axes are flipped which allows the energy to continue to positively flow from the pump to the signal and idler frequencies.
The most commonly used technique for creating quasi-phase-matched crystals is periodic poling
Periodic poling
Periodic poling is a formation of layers with alternate orientation in a birefringent material. The domains are regularly spaced, with period in a multiple of the desired wavelength of operation. The structure is desired to achieve quasi-phase-matching in the material.Periodically poled crystals...
.
Mathematical description
In nonlinear optics, the generation of other frequencies is the result of the nonlinear polarization response of the crystal due to fundamental pump frequency. When the crystal axis is flipped the polarization wave is shifted by 180 degrees thus ensuring that there is a positive energy flow to the signal and idler beam. In the case of Sum frequency generationSum frequency generation
Sum-frequency generation is a non-linear optical process. This phenomenon is based on the annihilation of two input photons at angular frequencies \omega_1 and \omega_2 while, simultaneously, one photon at frequency \omega_3 is generated...
polarization equation can be expressed by
Where
is the nonlinear susceptibility coefficient in which the sign of the coefficient is flipped when the crystal axis is flipped. Where 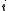represents the imaginary unitImaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
.
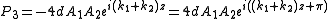
Development of signal amplitude
The following mathematical description assumes a constant pump amplitude. The signal wavelength can be expressed as a sum over the number of domains that exist in the crystal. In general the rate of change of the signal amplitude iswhere
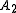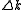is the generated frequency amplitude and is the pump frequency amplitude and is the phase mismatch between the two optical waves. The 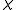refers to the nonlinear susceptibility of the crystal.In the case of a periodically poled crystal the optic axis is flipped by 180 degrees in every other domain, which changes the sign of
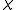. For the domain 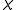can be expressed as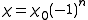where
is the index of the poled domain. The total signal amplitude 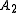can be expressed as a sum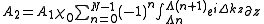which integrates to
and reduces to
The summation yields
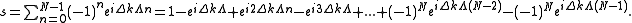
Multiply above equation both sides by a factor of
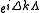
Adding both equation leads to the relation
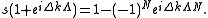
Solving for
gives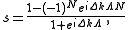which leads to
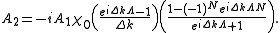
The total intensity can be expressed by
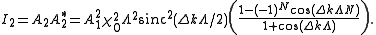
For the case of
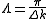the right part of the above equation is undefined so the limit needs to be taken when 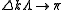by invoking L'Hôpital's ruleL'Hôpital's rule
In calculus, l'Hôpital's rule uses derivatives to help evaluate limits involving indeterminate forms. Application of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit...
.
Which leads to the signal intensity
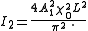
In order to allow different domain widths, ie.
, for , the above equation becomes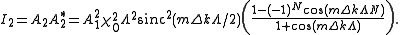With
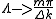the intensity becomes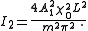This allows quasi-phase-matching to exist at different domain widths
.From this equation it is apparent, however, that as the quasi-phase match order
increases, the efficiency decreases by . For example for 3rd order quasi-phase matching only a third of the crystal is effectively used for the generation of signal frequency, as a consequence the amplitude of the signal wavelength only third of the amount of amplitude for same length crystal for 1st order quasi-phase match.Calculation of domain width
The domain width is calculated through the use of Sellmeier equationSellmeier equation
The Sellmeier equation is an empirical relationship between refractive index and wavelength for a particular transparent medium. The equation is used to determine the dispersion of light in the medium....
and using wavevector relations. In the case of DFG this relationship holds true
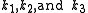where are the pump, signal, and idler wavevectors and . By calculating 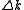for the different frequencies the domain width can be calculated from the relationship .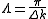