
Quasitriangular Hopf algebra
Encyclopedia
In mathematics
, a Hopf algebra
, H, is quasitriangular if there exists an invertible
element, R, of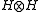 such that
such that
where ,
, 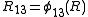 , and
, and 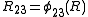 , where
, where 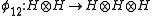 ,
,  , and
, and 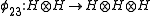 , are algebra morphisms determined by
, are algebra morphisms determined by
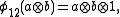

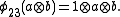
R is called the R-matrix.
As a consequence of the properties of quasitriangularity, the R-matrix, R, is a solution of the Yang-Baxter equation
(and so a module
V of H can be used to determine quasi-invariants of braids
, knots
and links
). Also as a consequence of the properties of quasitriangularity,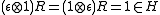 ; moreover
; moreover
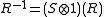 ,
, 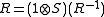 , and
, and 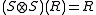 . One may further show that the
. One may further show that the
antipode S must be a linear isomorphism, and thus S^2 is an automorphism. In fact, S^2 is given by conjugating by an invertible element: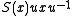 where
where 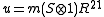 (cf. Ribbon Hopf algebra
(cf. Ribbon Hopf algebra
s).
It is possible to construct a quasitriangular Hopf algebra from a Hopf algebra and its dual, using the Drinfel'd
quantum double construction.
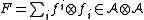 such that
such that 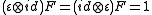 and satisfying the cocycle condition
and satisfying the cocycle condition
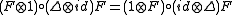
Furthermore, is invertible and the twisted antipode is given by
is invertible and the twisted antipode is given by 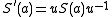 , with the twisted comultiplication, R-matrix and co-unit change according to those defined for the quasi-triangular Quasi-Hopf algebra
, with the twisted comultiplication, R-matrix and co-unit change according to those defined for the quasi-triangular Quasi-Hopf algebra
. Such a twist is known as an admissible (or Drinfel'd
) twist.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
, H, is quasitriangular if there exists an invertible
Inverse element
In abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
element, R, of
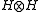 such that
such that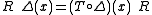 for all
for all 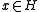 , where
, where 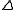 is the coproduct on H, and the linear map
is the coproduct on H, and the linear map 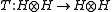 is given by
is given by 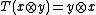 ,
,
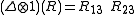 ,
,
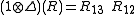 ,
,
where
 ,
, 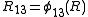 , and
, and 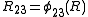 , where
, where 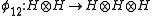 ,
,  , and
, and 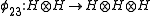 , are algebra morphisms determined by
, are algebra morphisms determined by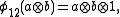

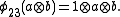
R is called the R-matrix.
As a consequence of the properties of quasitriangularity, the R-matrix, R, is a solution of the Yang-Baxter equation
Yang-Baxter equation
The Yang–Baxter equation is an equation which was first introduced in the field of statistical mechanics. It takes its name from independent work of C. N. Yang from 1968, and R. J. Baxter from 1971...
(and so a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
V of H can be used to determine quasi-invariants of braids
Braid theory
In topology, a branch of mathematics, braid theory is an abstract geometric theory studying the everyday braid concept, and some generalizations. The idea is that braids can be organized into groups, in which the group operation is 'do the first braid on a set of strings, and then follow it with a...
, knots
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
and links
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
). Also as a consequence of the properties of quasitriangularity,
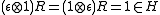 ; moreover
; moreover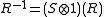 ,
, 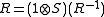 , and
, and 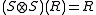 . One may further show that the
. One may further show that theantipode S must be a linear isomorphism, and thus S^2 is an automorphism. In fact, S^2 is given by conjugating by an invertible element:
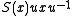 where
where 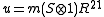 (cf. Ribbon Hopf algebra
(cf. Ribbon Hopf algebraRibbon Hopf algebra
A ribbon Hopf algebra is a quasitriangular Hopf algebra which possess an invertible central element \nu more commonly known as the ribbon element, such that the following conditions hold:...
s).
It is possible to construct a quasitriangular Hopf algebra from a Hopf algebra and its dual, using the Drinfel'd
Vladimir Drinfel'd
Vladimir Gershonovich Drinfel'd is a Ukrainian and Soviet mathematician at the University of Chicago.The work of Drinfeld related algebraic geometry over finite fields with number theory, especially the theory of automorphic forms, through the notions of elliptic module and the theory of the...
quantum double construction.
Twisting
The property of being a quasi-triangular Hopf algebra is preserved by twisting via an invertible element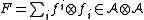 such that
such that 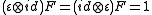 and satisfying the cocycle condition
and satisfying the cocycle condition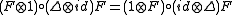
Furthermore,
 is invertible and the twisted antipode is given by
is invertible and the twisted antipode is given by 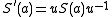 , with the twisted comultiplication, R-matrix and co-unit change according to those defined for the quasi-triangular Quasi-Hopf algebra
, with the twisted comultiplication, R-matrix and co-unit change according to those defined for the quasi-triangular Quasi-Hopf algebraQuasi-triangular Quasi-Hopf algebra
A quasi-triangular quasi-Hopf algebra is a specialized form of a quasi-Hopf algebra defined by the Ukrainian mathematician Vladimir Drinfeld in 1989...
. Such a twist is known as an admissible (or Drinfel'd
Vladimir Drinfel'd
Vladimir Gershonovich Drinfel'd is a Ukrainian and Soviet mathematician at the University of Chicago.The work of Drinfeld related algebraic geometry over finite fields with number theory, especially the theory of automorphic forms, through the notions of elliptic module and the theory of the...
) twist.

