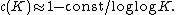The quotient of subspace theorem is an important property of finite dimensional normed spaces, discovered by Vitali Milman

Vitali Milman

Vitali Davidovich Milman is a mathematician specializing in analysis. He is currently a professor at the Tel-Aviv University. In the past he was a President of the Israel Mathematical Union and a member of the “Aliyah” committee of Tel-Aviv University.-Work:Milman received in Ph.D...

.

Let (X, ||·||) be an N-dimensional normed space. There exist subspaces Z ⊂ Y ⊂ X such that the following holds:

• The quotient space
  Quotient space (linear algebra)
  In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
  
   E = Y / Z is of dimension dim E ≥ c N, where c > 0 is a universal constant.
• The induced norm
  Norm (mathematics)
  In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
  
   || · || on E, defined by

is isomorphic

Isomorphism

In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations.  If there exists an isomorphism between two structures, the two structures are said to be isomorphic.  In a certain sense, isomorphic structures are...

 to Euclidean. That is, there exists a positive quadratic form

Quadratic form

In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....

("Euclidean structure") Q on E, such that

for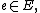

with K > 1 a universal constant.

In fact, the constant c can be made arbitrarily close to 1, at the expense of the
constant K becoming large. The original proof allowed