Ramanujan summation
Encyclopedia
Ramanujan summation is a technique invented by the mathematician Srinivasa Ramanujan
for assigning a sum to infinite divergent series
. Although the Ramanujan summation of a divergent series is not a sum in the traditional sense, it has properties which make it mathematically useful in the study of divergent infinite series, for which conventional summation is undefined.
Ramanujan summation essentially is a property of the partial sums, rather than a property of the entire sum, as that doesn't exist. If we take the Euler–Maclaurin summation formula together with the correction rule using Bernoulli number
s, we see that:
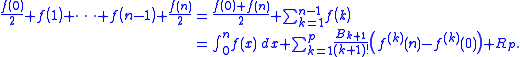
Ramanujan wrote it for the case p going to infinity:
where C is a constant specific to the series and its analytic continuation and the limits on the integral were not specified by Ramanujan, but presumably they were as given above. Comparing both formulae and assuming that R tends to 0 as x tends to infinity, we see that, in a general case, for functions f(x) with no divergence at x = 0: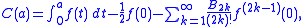
where Ramanujan assumed
. By taking 
we normally recover the usual summation for convergent series. For functions f(x) with no divergence at x = 1, we obtain: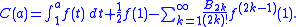
C(0) was then proposed to use as the sum of the divergent sequence. It is like a bridge between summation and integration. Using standard extensions for known divergent series, he calculated "Ramanujan summation" of those. In particular, the sum of is
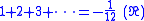
where the notation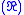
indicates Ramanujan summation. This formula originally appeared in one of Ramanujan's notebooks, without any notation to indicate that it was a Ramanujan summation.
For even powers we have:
and for odd powers we have a relation with the Bernoulli number
s:
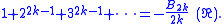
Those values are consistent with the Riemann zeta function.
More recently, the use of C(1) has been proposed as Ramanujan's summation, since then it can be assured that one series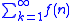
admits one and only one Ramanujan's summation, defined as the value in 1 of the only solution of the difference equation 
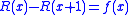that verifies the
condition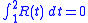
.
This new definition of Ramanujan's summation (denoted as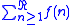
) does not coincide with the earlier defined Ramanujan's summation (C(0)) nor with the summation of convergent series, but it has interesting properties, such as:
If R(x) tends to a finite limit when x → +1, then the series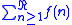
is convergent, and we have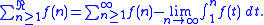
Another interesting result is this: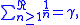
where
is the Euler–Mascheroni constant
.
Ramanujan resummation can be extended to integrals for example using the Euler-Maclaurin summation formula one can write
,
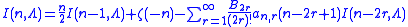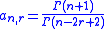
here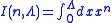
with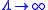 
the application of this Ramanujan resummation lends to finite results in the renormalization of Quantum Field theories
Srinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
for assigning a sum to infinite divergent series
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
. Although the Ramanujan summation of a divergent series is not a sum in the traditional sense, it has properties which make it mathematically useful in the study of divergent infinite series, for which conventional summation is undefined.
Ramanujan summation essentially is a property of the partial sums, rather than a property of the entire sum, as that doesn't exist. If we take the Euler–Maclaurin summation formula together with the correction rule using Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
s, we see that:
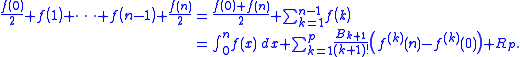
Ramanujan wrote it for the case p going to infinity:
where C is a constant specific to the series and its analytic continuation and the limits on the integral were not specified by Ramanujan, but presumably they were as given above. Comparing both formulae and assuming that R tends to 0 as x tends to infinity, we see that, in a general case, for functions f(x) with no divergence at x = 0:
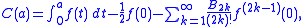
where Ramanujan assumed
. By taking we normally recover the usual summation for convergent series. For functions f(x) with no divergence at x = 1, we obtain:C(0) was then proposed to use as the sum of the divergent sequence. It is like a bridge between summation and integration. Using standard extensions for known divergent series, he calculated "Ramanujan summation" of those. In particular, the sum of is
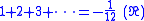
where the notation
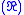indicates Ramanujan summation. This formula originally appeared in one of Ramanujan's notebooks, without any notation to indicate that it was a Ramanujan summation.For even powers we have:
and for odd powers we have a relation with the Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
s:
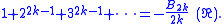
Those values are consistent with the Riemann zeta function.
More recently, the use of C(1) has been proposed as Ramanujan's summation, since then it can be assured that one series
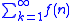admits one and only one Ramanujan's summation, defined as the value in 1 of the only solution of the difference equation 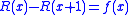that verifies thecondition
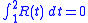.This new definition of Ramanujan's summation (denoted as
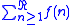) does not coincide with the earlier defined Ramanujan's summation (C(0)) nor with the summation of convergent series, but it has interesting properties, such as:If R(x) tends to a finite limit when x → +1, then the series
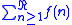is convergent, and we have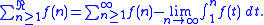Another interesting result is this:
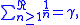
where
is the Euler–Mascheroni constantEuler–Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
.
Ramanujan resummation can be extended to integrals for example using the Euler-Maclaurin summation formula one can write
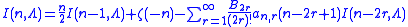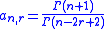
,here
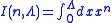with 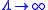the application of this Ramanujan resummation lends to finite results in the renormalization of Quantum Field theoriesSee also
- Borel summation
- Cesàro summationCesàro summationIn mathematical analysis, Cesàro summation is an alternative means of assigning a sum to an infinite series. If the series converges in the usual sense to a sum A, then the series is also Cesàro summable and has Cesàro sum A...
- Ramanujan's sum
- Divergent seriesDivergent seriesIn mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....