
Random Walker (Computer Vision)
Encyclopedia
The random walker algorithm is an algorithm for image segmentation. In the first description of the algorithm, a user interactively labels a small number of pixels with known labels (called seeds), e.g., "object" and "background". The unlabeled pixels are each imagined to release a random walker, and the probability is computed that each pixel's random walker first arrives at a seed bearing each label, i.e., if a user places K seeds, each with a different label, then it is necessary to compute, for each pixel, the probability that a random walker leaving the pixel will first arrive at each seed. This computation may be determined analytically by solving a system of linear equations. After computing these probabilities for each pixel, the pixel is assigned to the label for which it is most likely to send a random walker. The image is modeled as a graph
, in which each pixel corresponds to a node which is connected to neighboring pixels by edges, and the edges are weighted to reflect the similarity between the pixels. Therefore, the random walk occurs on the weighted graph (see Doyle and Snell for an introduction to random walks on graphs).
Although the initial algorithm was formulated as an interactive method for image segmentation, it has been extended to be a fully automatic algorithm, given a data fidelity term (e.g., an intensity prior). It has also been extended to other applications, such as Image Matching (R. Shen, I. Cheng, X.li and A. Basu), ICPR 2008, and Image Fusion, (R. Shen, I. Cheng, J.Shi and A. Basu), IEEE Trans. on Image Processing, 2011, and other applications.
The algorithm was initially published as a conference paper and later as a journal paper.
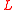 . The algorithm was shown to apply to an arbitrary number of labels (objects), but the exposition here is in terms of two labels (for simplicity of exposition).
. The algorithm was shown to apply to an arbitrary number of labels (objects), but the exposition here is in terms of two labels (for simplicity of exposition).
Assume that the image is represented by a graph
, with each node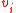 associated with a pixel and each edge
associated with a pixel and each edge 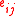 connecting neighboring pixels
connecting neighboring pixels 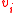 and
and 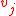 . The edge weights are used to encode node similarity, which may be derived from differences in image intensity, color, texture or any other meaningful features. For example, using image intensity
. The edge weights are used to encode node similarity, which may be derived from differences in image intensity, color, texture or any other meaningful features. For example, using image intensity 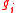 at node
at node 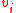 , it is common to use the edge weighting function
, it is common to use the edge weighting function
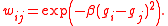
The nodes, edges and weights can then be used to construct the graph Laplacian matrix.
The random walker algorithm optimizes the energy
where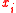 represents a real-valued variable associated with each node in the graph and the optimization is constrained by
represents a real-valued variable associated with each node in the graph and the optimization is constrained by  for
for 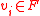 and
and  for
for 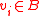 , where
, where  and
and  represent the sets of foreground and background seeds, respectively. If we let
represent the sets of foreground and background seeds, respectively. If we let 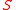 represent the set of nodes which are seeded (i.e.,
represent the set of nodes which are seeded (i.e., 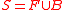 ) and
) and 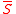 represent the set of unseeded nodes (i.e.,
represent the set of unseeded nodes (i.e., 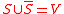 where
where 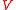 is the set of all nodes), then the optimum of the energy minimization problem is given by the solution to
is the set of all nodes), then the optimum of the energy minimization problem is given by the solution to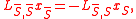
where the subscripts are used to indicate the portion of the graph Laplacian matrix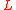 indexed by the respective sets.
indexed by the respective sets.
To incorporate likelihood (unary) terms into the algorithm, it was shown in that one may optimize the energy
for positive, diagonal matrices and
and  . Optimizing this energy leads to the system of linear equations
. Optimizing this energy leads to the system of linear equations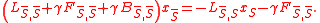
The set of seeded nodes,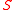 , may be empty in this case (i.e.,
, may be empty in this case (i.e.,  ), but the presence of the positive diagonal matrices allows for a unique solution to this linear system.
), but the presence of the positive diagonal matrices allows for a unique solution to this linear system.
For example, if the likelihood/unary terms are used to incorporate a color model of the object, then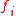 would represent the confidence that the color at node
would represent the confidence that the color at node 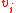 would belong to object (i.e., a larger value of
would belong to object (i.e., a larger value of 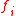 indicates greater confidence that
indicates greater confidence that 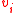 belonged to the object label) and
belonged to the object label) and 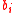 would represent the confidence that the color at node
would represent the confidence that the color at node 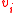 belongs to the background.
belongs to the background.
. The resistance,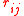 , associated with edge
, associated with edge 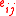 is set equal to
is set equal to  (i.e., the edge weight equals electrical conductance).
(i.e., the edge weight equals electrical conductance).
In the first interpretation, each node associated with a background seed,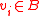 , is tied directly to ground
, is tied directly to ground
while each node associated with an object/foreground seed,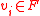 is attached to a unit direct current
is attached to a unit direct current
ideal voltage source
tied to ground (i.e., to establish a unit potential at each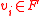 ). The steady-state electrical circuit potentials established at each node by this circuit configuration will exactly equal the random walker probabilities. Specifically, the electrical potential,
). The steady-state electrical circuit potentials established at each node by this circuit configuration will exactly equal the random walker probabilities. Specifically, the electrical potential, 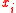 at node
at node 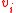 will equal the probability that a random walker dropped at node
will equal the probability that a random walker dropped at node 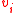 will reach an object/foreground node before reaching a background node.
will reach an object/foreground node before reaching a background node.
In the second interpretation, labeling a node as object or background by thresholding the random walker probability at 0.5 is equivalent to labeling a node as object or background based on the relative effective conductance between the node and the object or background seeds. Specifically, if a node has a higher effective conductance (lower effective resistance) to the object seeds than to the background seeds, then node is labeled as object. If a node has a higher effective conductance (lower effective resistance) to the background seeds than to the object seeds, then node is labeled as background.
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
, in which each pixel corresponds to a node which is connected to neighboring pixels by edges, and the edges are weighted to reflect the similarity between the pixels. Therefore, the random walk occurs on the weighted graph (see Doyle and Snell for an introduction to random walks on graphs).
Although the initial algorithm was formulated as an interactive method for image segmentation, it has been extended to be a fully automatic algorithm, given a data fidelity term (e.g., an intensity prior). It has also been extended to other applications, such as Image Matching (R. Shen, I. Cheng, X.li and A. Basu), ICPR 2008, and Image Fusion, (R. Shen, I. Cheng, J.Shi and A. Basu), IEEE Trans. on Image Processing, 2011, and other applications.
The algorithm was initially published as a conference paper and later as a journal paper.
Mathematics
Although the algorithm was described in terms of random walks, the probability that each node sends a random walker to the seeds may be calculated analytically by solving a sparse, positive-definite system of linear equations with the graph Laplacian matrix, which we may represent with the variable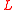 . The algorithm was shown to apply to an arbitrary number of labels (objects), but the exposition here is in terms of two labels (for simplicity of exposition).
. The algorithm was shown to apply to an arbitrary number of labels (objects), but the exposition here is in terms of two labels (for simplicity of exposition).Assume that the image is represented by a graph
Graph
Graph may refer to:* A graphic depicting the relationship between two or more variables used, for instance, in visualising scientific data.In mathematics:* Graph , is a set of vertices and edges....
, with each node
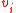 associated with a pixel and each edge
associated with a pixel and each edge 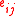 connecting neighboring pixels
connecting neighboring pixels 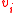 and
and 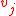 . The edge weights are used to encode node similarity, which may be derived from differences in image intensity, color, texture or any other meaningful features. For example, using image intensity
. The edge weights are used to encode node similarity, which may be derived from differences in image intensity, color, texture or any other meaningful features. For example, using image intensity 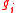 at node
at node 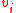 , it is common to use the edge weighting function
, it is common to use the edge weighting function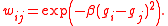
The nodes, edges and weights can then be used to construct the graph Laplacian matrix.
The random walker algorithm optimizes the energy

where
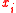 represents a real-valued variable associated with each node in the graph and the optimization is constrained by
represents a real-valued variable associated with each node in the graph and the optimization is constrained by  for
for 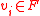 and
and  for
for 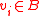 , where
, where  and
and  represent the sets of foreground and background seeds, respectively. If we let
represent the sets of foreground and background seeds, respectively. If we let 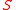 represent the set of nodes which are seeded (i.e.,
represent the set of nodes which are seeded (i.e., 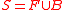 ) and
) and 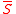 represent the set of unseeded nodes (i.e.,
represent the set of unseeded nodes (i.e., 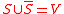 where
where 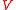 is the set of all nodes), then the optimum of the energy minimization problem is given by the solution to
is the set of all nodes), then the optimum of the energy minimization problem is given by the solution to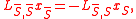
where the subscripts are used to indicate the portion of the graph Laplacian matrix
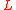 indexed by the respective sets.
indexed by the respective sets.To incorporate likelihood (unary) terms into the algorithm, it was shown in that one may optimize the energy

for positive, diagonal matrices
 and
and  . Optimizing this energy leads to the system of linear equations
. Optimizing this energy leads to the system of linear equations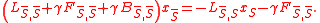
The set of seeded nodes,
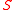 , may be empty in this case (i.e.,
, may be empty in this case (i.e.,  ), but the presence of the positive diagonal matrices allows for a unique solution to this linear system.
), but the presence of the positive diagonal matrices allows for a unique solution to this linear system.For example, if the likelihood/unary terms are used to incorporate a color model of the object, then
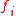 would represent the confidence that the color at node
would represent the confidence that the color at node 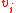 would belong to object (i.e., a larger value of
would belong to object (i.e., a larger value of 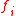 indicates greater confidence that
indicates greater confidence that 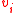 belonged to the object label) and
belonged to the object label) and 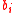 would represent the confidence that the color at node
would represent the confidence that the color at node 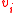 belongs to the background.
belongs to the background.Algorithm interpretations
The random walker algorithm was initially motivated by labeling a pixel as object/background based on the probability that a random walker dropped at the pixel would first reach an object (foreground) seed or a background seed. However, there are several other interpretations of this same algorithm which have appeared in .Circuit theory interpretations
There are well-known connections between electrical circuit theory and random walks on graphs. Consequently, the random walker algorithm has two different interpretations in terms of an electric circuit. In both cases, the graph is viewed as an electric circuit in which each edge is replaced by a passive linear resistorResistor
A linear resistor is a linear, passive two-terminal electrical component that implements electrical resistance as a circuit element.The current through a resistor is in direct proportion to the voltage across the resistor's terminals. Thus, the ratio of the voltage applied across a resistor's...
. The resistance,
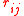 , associated with edge
, associated with edge 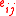 is set equal to
is set equal to  (i.e., the edge weight equals electrical conductance).
(i.e., the edge weight equals electrical conductance).In the first interpretation, each node associated with a background seed,
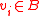 , is tied directly to ground
, is tied directly to groundGround (electricity)
In electrical engineering, ground or earth may be the reference point in an electrical circuit from which other voltages are measured, or a common return path for electric current, or a direct physical connection to the Earth....
while each node associated with an object/foreground seed,
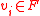 is attached to a unit direct current
is attached to a unit direct currentDirect current
Direct current is the unidirectional flow of electric charge. Direct current is produced by such sources as batteries, thermocouples, solar cells, and commutator-type electric machines of the dynamo type. Direct current may flow in a conductor such as a wire, but can also flow through...
ideal voltage source
Voltage source
In electric circuit theory, an ideal voltage source is a circuit element where the voltage across it is independent of the current through it. A voltage source is the dual of a current source. In analysis, a voltage source supplies a constant DC or AC potential between its terminals for any current...
tied to ground (i.e., to establish a unit potential at each
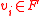 ). The steady-state electrical circuit potentials established at each node by this circuit configuration will exactly equal the random walker probabilities. Specifically, the electrical potential,
). The steady-state electrical circuit potentials established at each node by this circuit configuration will exactly equal the random walker probabilities. Specifically, the electrical potential, 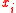 at node
at node 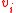 will equal the probability that a random walker dropped at node
will equal the probability that a random walker dropped at node 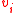 will reach an object/foreground node before reaching a background node.
will reach an object/foreground node before reaching a background node.In the second interpretation, labeling a node as object or background by thresholding the random walker probability at 0.5 is equivalent to labeling a node as object or background based on the relative effective conductance between the node and the object or background seeds. Specifically, if a node has a higher effective conductance (lower effective resistance) to the object seeds than to the background seeds, then node is labeled as object. If a node has a higher effective conductance (lower effective resistance) to the background seeds than to the object seeds, then node is labeled as background.
Extensions
The traditional random walker algorithm described above has been extended in several ways:- Random walks with restart
- Alpha matting
- Threshold selection
- Soft inputs
- Run on a presegmented image
- Scale space random walk
- Fast random walker using offline precomputationPrecomputationIn algorithms, precomputation is the act of performing an initial computation before run time to generate a lookup table that can be used by an algorithm to avoid repeated computation each time it is executed. Precomputation is often used in algorithms that depend on the results of expensive...
Applications
Beyond image segmentation, the random walker algorithm has been additionally applied to several problems in computer vision and graphics:- Image Colorization
- Interactive rotoscoping
- Medical image segmentation
- Merging multiple segmentations
- Mesh segmentation
- Mesh denoising
- Segmentation editing
- Shadow elimination
- Image matching
- Image Fusion

