Range ambiguity resolution
Encyclopedia
Range ambiguity resolution is a technique used with medium Pulse repetition frequency
(PRF) radar to obtain range information for distances that exceed the distance between transmit pulses.
This signal processing technique is required with pulse-Doppler radar
.
The raw return signal from a reflection will appear to be arriving from a distance less than the true range of the reflection when the wave-length of the pulse repetition frequency (PRF) exceeds the range of the reflection. This causes reflected signals to be folded, so that the apparent range is a modulo function
of true range.
(PRF).
Range ambiguity resolution is required to obtain the true range when the measurements is made using a system where the following inequality is true.
The range measurements made in this way produces a modulo
function of the true range.
Suppose a two PRF combination is chosen where the distance between transmit pulses (pulse spacing) is different by the pulse width of the transmitter.
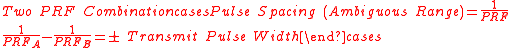
Each transmit pulse is separated in distance the ambiguous range interval. Multiple samples are taken between transmit pulses.
If the receive signal falls in the same sample number for both PRF, then the object is in the first ambiguous range interval. If the receive signal falls into sample numbers that are different by one, then the object is in the second ambiguous range interval. If the receive signal falls into sample numbers that are different by two, then the object is in the third ambiguous range interval.
The general constraints for range performance are as follows.
Each sample is processed to determine if there is a reflected signal (detection). This is called signal detection.
The detection made using both PRF can be compared to identify the true range. This comparison depends upon the transmitter duty cycle (the ratio between on and off).
The duty cycle
is the ratio of the width of the transmit pulse width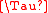
and the period between pulses 
.
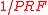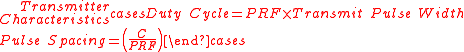
Pulse-Doppler can reliably resolve true range at all distances less than the Instrumented Range. The optimum pair of PRF used for a pulse-Doppler detection scheme must be different by a minimum of
. This makes the range of each PRF different by the width of the sample period.
The difference between the sample numbers where for reflection signal is found for these two PRF will be about the same as the number of the ambiguous range intervals between the radar and the reflector (i.e.: if the reflection falls in sample 3 for PRF 1 and in sample 5 for PRF 2, then the reflector is in ambiguous range interval 2=5-3).
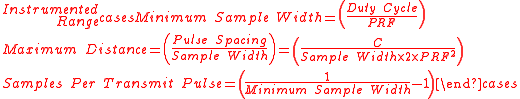
There is no guarantee that true range will be found for objects beyond this distance.
.
Each ambiguous range sample contains the receive signal from multiple different range locations. Ambiguity processing determines the true range.
This is explained best using the following example, where PRF A produces a transmit pulse every 6 km and PRF B produces a transmit pulse every 5 km.
The apparent range for PRF A falls in the 2 km sample, and the apparent range for PRF B falls in the 4 km sample. This combination places the true target distance at 14 km (2x6+2 or 2x5+4). This can be seen graphically when range intervals are stacked end-to-end as shown below.
"A" represents target range possibilities for PRF A, and "B" represents target range possibilities for PRF B.
This process uses a look-up table when there is only one detection. The size of the table limits the maximum range.
The process shown above is a type of digital convolution
algorithm.
The process described above is slightly more complex in real systems because more than one detection signal can occur within the radar beam. The pulse rate must alternate rapidly between at least 4 different PRF to handle these complexities.
, where the radar can be blind for some combinations of speed and distance.
A four PRF scheme is generally used with two pair of PRF for the detection process so that blind zones are eliminated.
The antenna must dwell in the same position for at least three different PRF.
that requires additional information and additional processing.
This is accommodated by sorting detections in order of amplitude. Ambiguity resolution relies on processing detections with similar size together as a group.
Pulse repetition frequency
Pulse repetition frequency or Pulse repetition rate is the number of pulses per time unit . It is a measure or specification mostly used within various technical disciplines Pulse repetition frequency (PRF) or Pulse repetition rate (PRR) is the number of pulses per time unit (e.g. Seconds). It...
(PRF) radar to obtain range information for distances that exceed the distance between transmit pulses.
This signal processing technique is required with pulse-Doppler radar
Pulse-doppler radar
Pulse-Doppler is a 4D radar system capable of detecting both target 3D location as well as measuring radial velocity . It uses the Doppler effect to avoid overloading computers and operators as well as to reduce power consumption...
.
The raw return signal from a reflection will appear to be arriving from a distance less than the true range of the reflection when the wave-length of the pulse repetition frequency (PRF) exceeds the range of the reflection. This causes reflected signals to be folded, so that the apparent range is a modulo function
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
of true range.
Definition
Range aliasing occurs when reflections arrive from distances that exceed the wavelength of the pulse repetition frequencyPulse repetition frequency
Pulse repetition frequency or Pulse repetition rate is the number of pulses per time unit . It is a measure or specification mostly used within various technical disciplines Pulse repetition frequency (PRF) or Pulse repetition rate (PRR) is the number of pulses per time unit (e.g. Seconds). It...
(PRF).
Range ambiguity resolution is required to obtain the true range when the measurements is made using a system where the following inequality is true.
The range measurements made in this way produces a modulo
Modulo
In the mathematical community, the word modulo is often used informally. Generally, to say "A is the same as B modulo C" means, more-or-less, "A and B are the same except for differences accounted for or explained by C"....
function of the true range.
Theory
To find the true range, the radar must measure the apparent range using two or more different PRF.Suppose a two PRF combination is chosen where the distance between transmit pulses (pulse spacing) is different by the pulse width of the transmitter.
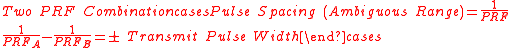
Each transmit pulse is separated in distance the ambiguous range interval. Multiple samples are taken between transmit pulses.
If the receive signal falls in the same sample number for both PRF, then the object is in the first ambiguous range interval. If the receive signal falls into sample numbers that are different by one, then the object is in the second ambiguous range interval. If the receive signal falls into sample numbers that are different by two, then the object is in the third ambiguous range interval.
The general constraints for range performance are as follows.
Each sample is processed to determine if there is a reflected signal (detection). This is called signal detection.
The detection made using both PRF can be compared to identify the true range. This comparison depends upon the transmitter duty cycle (the ratio between on and off).
The duty cycle
Duty cycle
In engineering, the duty cycle of a machine or system is the time that it spends in an active state as a fraction of the total time under consideration....
is the ratio of the width of the transmit pulse width
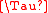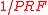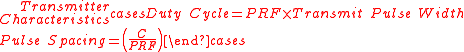
and the period between pulses .Pulse-Doppler can reliably resolve true range at all distances less than the Instrumented Range. The optimum pair of PRF used for a pulse-Doppler detection scheme must be different by a minimum of
. This makes the range of each PRF different by the width of the sample period.The difference between the sample numbers where for reflection signal is found for these two PRF will be about the same as the number of the ambiguous range intervals between the radar and the reflector (i.e.: if the reflection falls in sample 3 for PRF 1 and in sample 5 for PRF 2, then the reflector is in ambiguous range interval 2=5-3).
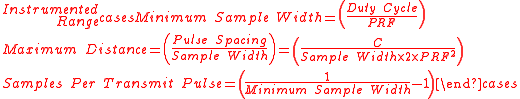
There is no guarantee that true range will be found for objects beyond this distance.
Operation
The following is a special case of the Chinese remainder theoremChinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
.
Each ambiguous range sample contains the receive signal from multiple different range locations. Ambiguity processing determines the true range.
This is explained best using the following example, where PRF A produces a transmit pulse every 6 km and PRF B produces a transmit pulse every 5 km.
| Transmit | 1 km Sample | 2 km Sample | 3 km Sample | 4 km Sample | 5 km Sample |
|---|---|---|---|---|---|
| Target PRF A | |||||
| Target PRF B |
The apparent range for PRF A falls in the 2 km sample, and the apparent range for PRF B falls in the 4 km sample. This combination places the true target distance at 14 km (2x6+2 or 2x5+4). This can be seen graphically when range intervals are stacked end-to-end as shown below.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 29 | 29 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | A | A | A | A | |||||||||||||||||||||||||
| B | B | B | B | B | B |
"A" represents target range possibilities for PRF A, and "B" represents target range possibilities for PRF B.
This process uses a look-up table when there is only one detection. The size of the table limits the maximum range.
The process shown above is a type of digital convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
algorithm.
Limitations
This technique has two limitations.- Blind Zones
- Multiple Targets
The process described above is slightly more complex in real systems because more than one detection signal can occur within the radar beam. The pulse rate must alternate rapidly between at least 4 different PRF to handle these complexities.
Blind Zones
Each individual PRF has blind ranges, where the transmitter pulse occurs at the same time as the target reflection signal arrives back at the radar. Each individual PRF has blind velocities where the velocity of the aircraft will appear stationary. This causes scallopingRadar scalloping
Scalloping is a radar phenomenon that reduces sensitivity for certain distance and velocity combinations.The name is derived from the appearance of areas that are scooped out of graphs that indicate radar sensitivity....
, where the radar can be blind for some combinations of speed and distance.
- Radar scalloping detailed explanation
A four PRF scheme is generally used with two pair of PRF for the detection process so that blind zones are eliminated.
The antenna must dwell in the same position for at least three different PRF.
Multiple Targets
Multiple aircraft within the radar beam that are separated by over 500 meters introduces additional degrees of freedomDegrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
that requires additional information and additional processing.
This is accommodated by sorting detections in order of amplitude. Ambiguity resolution relies on processing detections with similar size together as a group.