Rayleigh-Taylor instability
Encyclopedia
Instability
In numerous fields of study, the component of instability within a system is generally characterized by some of the outputs or internal states growing without bounds...
of an interface
Interface (chemistry)
An interface is a surface forming a common boundary among two different phases, such as an insoluble solid and a liquid, two immiscible liquids or a liquid and an insoluble gas. The importance of the interface depends on which type of system is being treated: the bigger the quotient area/volume,...
between two fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
s of different densities
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
, which occurs when the lighter fluid is pushing the heavier fluid.
This is the case with an interstellar cloud and shock system. The equivalent situation occurs when gravity is acting on two fluids of different density – with the dense fluid above a fluid of lesser density – such as water balancing on light oil.
Consider two completely plane-parallel layers of immiscible fluid, the heavier on top of the light one and both subject to the Earth's gravity. The equilibrium
Mechanical equilibrium
A standard definition of static equilibrium is:This is a strict definition, and often the term "static equilibrium" is used in a more relaxed manner interchangeably with "mechanical equilibrium", as defined next....
here is unstable to certain perturbations
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
or disturbances. An unstable disturbance will grow and lead to a release of potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
, as the heavier material moves down under the (effective) gravitational field, and the lighter material is displaced upwards. This was the set-up as studied by Lord Rayleigh. The important insight by G. I. Taylor was, that he realised this situation is equivalent to the situation when the fluids are accelerated
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
(without gravity), with the lighter fluid accelerating into the heavier fluid. This can be experienced, for example, by accelerating a glass of water downward faster than the Earth's gravitational acceleration.
As the instability develops, downward-moving irregularities ('dimples') are quickly magnified into sets of inter-penetrating Rayleigh–Taylor fingers. Therefore the Rayleigh–Taylor instability is sometimes qualified to be a fingering instability. The upward-moving, lighter material is shaped like mushroom caps.
This process is evident not only in many terrestrial examples, from salt dome
Salt dome
A salt dome is a type of structural dome formed when a thick bed of evaporite minerals found at depth intrudes vertically into surrounding rock strata, forming a diapir....
s to weather inversions, but also in astrophysics
Astrophysics
Astrophysics is the branch of astronomy that deals with the physics of the universe, including the physical properties of celestial objects, as well as their interactions and behavior...
and electrohydrodynamics
Electrohydrodynamics
Electrohydrodynamics , also known as electro-fluid-dynamics or electrokinetics, is the study of the dynamics of electrically charged fluids. It is the study of the motions of ionised particles or molecules and their interactions with electric fields and the surrounding fluid...
. RT fingers are especially obvious in the Crab Nebula
Crab Nebula
The Crab Nebula is a supernova remnant and pulsar wind nebula in the constellation of Taurus...
, in which the expanding pulsar wind nebula
Pulsar wind nebula
A pulsar wind nebula is a nebula powered by the pulsar wind of a pulsar. At the early stages of their evolution, pulsar wind nebulae are often found inside the shells of supernova remnants...
powered by the Crab pulsar
Crab Pulsar
The Crab Pulsar is a relatively young neutron star. The star is the central star in the Crab Nebula, a remnant of the supernova SN 1054, which was widely observed on Earth in the year 1054...
is sweeping up ejected material from the supernova
Supernova
A supernova is a stellar explosion that is more energetic than a nova. It is pronounced with the plural supernovae or supernovas. Supernovae are extremely luminous and cause a burst of radiation that often briefly outshines an entire galaxy, before fading from view over several weeks or months...
explosion 1000 years ago.
Note that the RT instability is not to be confused with the Plateau-Rayleigh instability
Plateau-Rayleigh instability
The Plateau–Rayleigh instability, often just called the Rayleigh instability, explains why and how a falling stream of fluid breaks up into smaller packets with the same volume but less surface area. It is related to the Rayleigh–Taylor instability...
(also known as Rayleigh instability) of a liquid jet. This instability, sometimes called the hosepipe (or firehose) instability, occurs due to surface tension, which acts to break a cylindrical jet into a stream of droplets having the same volume but lower surface area.
Linear stability analysis
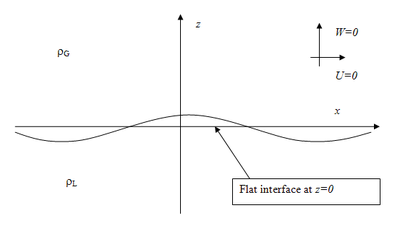
where the gravitationalEarth's gravity
The gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
field is
An interface at 
separates the fluids of densitiesDensity
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
in the upper region, and 
in the lower region. In this section it is shown that when the heavy fluid sits on top, the growth of a small perturbation at the interface is exponentialExponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
, and takes place at the rate
where
is the temporal growth rate, 
is the spatial wavenumberWavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
and
is the Atwood number.The perturbation introduced to the system is described by a velocity field of infinitesimally small amplitude,
Because the fluid is assumed incompressible, this velocity field has the streamfunction representation
where the subscripts indicate partial derivatives. Moreover, in an initially stationary incompressible fluid, there is no vorticity, and the fluid stays irrotational, hence
. In the streamfunction representation, 
Next, because of the translational invariance of the system in the x-direction, it is possible to make the ansatzAnsatz
Ansatz is a German noun with several meanings in the English language.It is widely encountered in physics and mathematics literature.Since ansatz is a noun, in German texts the initial a of this word is always capitalised.-Definition:...
where
is a spatial wavenumber. Thus, the problem reduces to solving the equation
The domain of the problem is the following: the fluid with label 'L' lives in the region
, while the fluid with the label 'G' lives in the upper half-plane 
. To specify the solution fully, it is necessary to fix conditions at the boundaries and interface. This determines the wave speed c, which in turn determines the stability properties of the system.The first of these conditions is provided by details at the boundary. The perturbation velocities
should satisfy a no-flux condition, so that fluid does not leak out at the boundaries 
Thus, 
on 
, and 
on 
. In terms of the streamfunction, this is
The other three conditions are provided by details at the interface
.Continuity of vertical velocity: At
, the vertical velocities match, 
. Using the streamfunction representation, this gives
Expanding about
gives
where H.O.T. means 'higher-order terms'. This equation is the required interfacial condition.
The free-surface condition: At the free surface
, the kinematic condition holds:
Linearizing, this is simply
where the velocity
is linearized on to the surface 
. Using the normal-mode and streamfunction representations, this condition is 
, the second interfacial condition.Pressure relation across the interface: For the case with surface tension
Surface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
, the pressure difference over the interface at
is given by the Young–Laplace equation:
where σ is the surface tension and κ is the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of the interface, which in a linear approximation is
Thus,
However, this condition refers to the total pressure (base+perturbed), thus
(As usual, The perturbed quantities can be linearized onto the surface z=0.) Using hydrostatic balance, in the form
this becomes
The perturbed pressures are evaluated in terms of streamfunctions, using the horizontal momentum equation of the linearised Euler equations for the perturbations,
-
with 
to yield
Putting this last equation and the jump condition on
together,
Substituting the second interfacial condition
and using the normal-mode representation, this relation becomes
where there is no need to label
(only its derivatives) because 
at
Solution
Now that the model of stratified flow has been set up, the solution is at hand. The streamfunction equation
with the boundary conditions 
has the solution
The first interfacial condition states that
at 
, which forces 
The third interfacial condition states that
Plugging the solution into this equation gives the relation
The A cancels from both sides and we are left with
To understand the implications of this result in full, it is helpful to consider the case of zero surface tension. Then,
and clearly
- If
, 
and c is real. This happens when the
lighter fluid sits on top;
- If
, 
and c is purely imaginary. This happens
when the heavier fluid sits on top.
Now, when the heavier fluid sits on top,
, and
where
is the Atwood number. By taking the positive solution, we see that the solution has the form
and this is associated to the interface position η by:
Now define 
initially at 
is given by:
which grows exponentially in time. Here B is the amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of the initial perturbation, and
denotes the real part of the complex valuedComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
expression between brackets.
In general, the condition for linear instability is that the imaginary part of the "wave speed" c be positive. Finally, restoring the surface tension makes c2 less negative and is therefore stabilizing. Indeed, there is a range of short waves for which the surface tension stabilizes the system and prevents the instability forming.
Late-time behaviour
The analysis of the previous section breaks down when the amplitude of the perturbation is large. The growth then becomes non-linear as the spikes and bubbles of the instability tangle and roll up into vortices. Then, as in the figure, numerical simulationComputational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
of the full problem is required to describe the system.
See also
- Richtmyer-Meshkov instabilityRichtmyer-Meshkov instabilityThe Richtmyer–Meshkov instability occurs when an interface between fluids of differing density is impulsively accelerated, e.g. by the passage of a shock wave. The development of the instability begins with small amplitude perturbations which initially grow linearly with time...
- Kelvin–Helmholtz instability
- Mushroom cloudMushroom cloudA mushroom cloud is a distinctive pyrocumulus mushroom-shaped cloud of condensed water vapor or debris resulting from a very large explosion. They are most commonly associated with nuclear explosions, but any sufficiently large blast will produce the same sort of effect. They can be caused by...
- Plateau-Rayleigh instabilityPlateau-Rayleigh instabilityThe Plateau–Rayleigh instability, often just called the Rayleigh instability, explains why and how a falling stream of fluid breaks up into smaller packets with the same volume but less surface area. It is related to the Rayleigh–Taylor instability...
- Salt fingeringSalt fingeringSalt fingering is a mixing process that occurs when relatively warm, salty water overlies relatively colder, fresher water. It is driven by the fact that heated water diffuses more readily than salty water...
- Hydrodynamic stabilityHydrodynamic stabilityIn fluid dynamics, hydrodynamic stability is the field which analyses the stability and the onset of instability of fluid flows. Instabilities may develop further into turbulence....
- Kármán vortex street