
Real structure
Encyclopedia
In mathematics
, a real structure on a complex
vector space
is a way to decompose the complex vector space in the direct sum of two real
vector spaces. The prototype of such a structure is the field of complex numbers itself, considered as a complex vector space over itself and with the conjugation map
 , with
, with 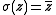 , giving the "canonical" real structure on
, giving the "canonical" real structure on 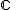 , that is
, that is 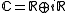 .
.
The conjugation map is antilinear: and
and  .
.
V is an antilinear involution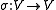 . A real structure defines a real subspace
. A real structure defines a real subspace  , its fix locus, and the natural map
, its fix locus, and the natural map
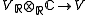
is an isomorphism. Conversely any vector space that is the complexification
of a real vector space has a natural real structure.
One first notes that every complex space V has a real form obtained by taking the same vectors as in the original set and restricting the scalars to be real. If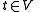 and
and 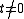 then the vectors
then the vectors  and
and 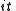 are linear independent
are linear independent
in the real form of V. Hence:
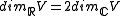
Naturally, one would wish to represent V as the direct sum of two real vector spaces, the "real and imaginary parts of V". There is no canonical way of doing this: such a splitting is an additional real structure in V. It may be introduced as follows. Let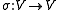 be an antilinear map such that
be an antilinear map such that 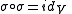 , that is an antilinear involution of the complex space V.
, that is an antilinear involution of the complex space V.
Any vector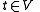 can be written
can be written 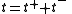 ,
,
where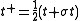 and
and 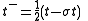 .
.
Therefore, one gets a direct sum
of vector spaces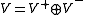 where:
where:
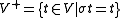 and
and 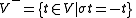 .
.
Both sets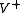 and
and 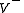 are real vector space
are real vector space
s. The linear map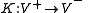 , where
, where 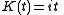 , is an isomorphism of real vector spaces, whence:
, is an isomorphism of real vector spaces, whence:
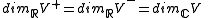 .
.
The first factor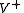 is also denoted by
is also denoted by 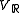 and is left invariant by
and is left invariant by 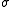 , that is
, that is 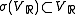 . The second factor
. The second factor 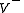 is
is
usually denoted by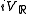 . The direct sum
. The direct sum 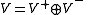 reads now as:
reads now as:
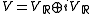 ,
,
i.e. as the direct sum of the "real"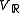 and "imaginary"
and "imaginary" 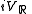 parts of V. This construction strongly depends on the choice of an antilinear involution
parts of V. This construction strongly depends on the choice of an antilinear involution
of the complex vector space V. The complexification
of the real vector space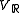 , i.e.,
, i.e.,
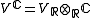 admits
admits
a natural real structure and hence is canonically isomorphic to the direct sum of two copies of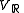 :
:
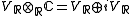 .
.
It follows a natural linear isomorphism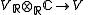 between complex vector spaces with a given real structure.
between complex vector spaces with a given real structure.
A real structure on a complex vector space V, that is an antilinear involution
 , may be equivalently described in terms of the linear map
, may be equivalently described in terms of the linear map 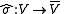 from the vector space
from the vector space  to the complex conjugate vector space
to the complex conjugate vector space
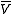 defined by
defined by
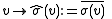 .
.
defined over a subfield of the real numbers,
the real structure is the complex conjugation acting on the points of the variety in complex projective or affine space.
Its fixed locus are the space of real points of the variety (which may be empty).
is in a natural way a member of the Galois group
of the algebraic closure
of the basefield.
The real structure is the Galois action of this conjugation on the extension of the
scheme over the algebraic closure of the base field.
The real points are the points whose residue field is fixed (which may be empty).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a real structure on a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
is a way to decompose the complex vector space in the direct sum of two real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector spaces. The prototype of such a structure is the field of complex numbers itself, considered as a complex vector space over itself and with the conjugation map
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
 , with
, with 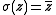 , giving the "canonical" real structure on
, giving the "canonical" real structure on 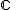 , that is
, that is 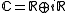 .
.The conjugation map is antilinear:
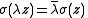 and
and  .
.Vector space
A real structure on a complex vector spaceComplex vector space
A complex vector space is a vector space over the complex numbers. It can also refer to:* a vector space over the real numbers with a linear complex structure...
V is an antilinear involution
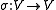 . A real structure defines a real subspace
. A real structure defines a real subspace  , its fix locus, and the natural map
, its fix locus, and the natural map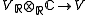
is an isomorphism. Conversely any vector space that is the complexification
Complexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
of a real vector space has a natural real structure.
One first notes that every complex space V has a real form obtained by taking the same vectors as in the original set and restricting the scalars to be real. If
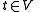 and
and 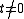 then the vectors
then the vectors  and
and 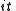 are linear independent
are linear independentLinear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
in the real form of V. Hence:
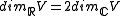
Naturally, one would wish to represent V as the direct sum of two real vector spaces, the "real and imaginary parts of V". There is no canonical way of doing this: such a splitting is an additional real structure in V. It may be introduced as follows. Let
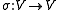 be an antilinear map such that
be an antilinear map such that 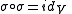 , that is an antilinear involution of the complex space V.
, that is an antilinear involution of the complex space V.Any vector
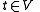 can be written
can be written 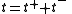 ,
,where
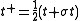 and
and 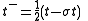 .
.Therefore, one gets a direct sum
Direct sum
In mathematics, one can often define a direct sum of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets , together with a suitably defined structure. More abstractly, the direct sum is often, but not always, the coproduct in the category in question...
of vector spaces
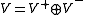 where:
where: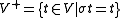 and
and 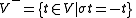 .
.Both sets
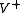 and
and 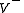 are real vector space
are real vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s. The linear map
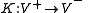 , where
, where 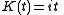 , is an isomorphism of real vector spaces, whence:
, is an isomorphism of real vector spaces, whence: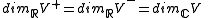 .
.The first factor
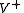 is also denoted by
is also denoted by 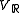 and is left invariant by
and is left invariant by 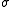 , that is
, that is 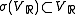 . The second factor
. The second factor 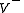 is
isusually denoted by
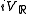 . The direct sum
. The direct sum 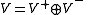 reads now as:
reads now as: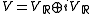 ,
,i.e. as the direct sum of the "real"
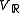 and "imaginary"
and "imaginary" 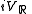 parts of V. This construction strongly depends on the choice of an antilinear involution
parts of V. This construction strongly depends on the choice of an antilinear involutionInvolution
In mathematics, an involution, or an involutary function, is a function f that is its own inverse:-General properties:Any involution is a bijection.The identity map is a trivial example of an involution...
of the complex vector space V. The complexification
Complexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
of the real vector space
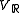 , i.e.,
, i.e.,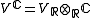 admits
admitsa natural real structure and hence is canonically isomorphic to the direct sum of two copies of
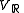 :
: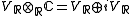 .
.It follows a natural linear isomorphism
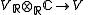 between complex vector spaces with a given real structure.
between complex vector spaces with a given real structure.A real structure on a complex vector space V, that is an antilinear involution
Involution
In mathematics, an involution, or an involutary function, is a function f that is its own inverse:-General properties:Any involution is a bijection.The identity map is a trivial example of an involution...
 , may be equivalently described in terms of the linear map
, may be equivalently described in terms of the linear map 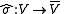 from the vector space
from the vector space  to the complex conjugate vector space
to the complex conjugate vector spaceComplex conjugate vector space
In mathematics, the complex conjugate of a complex vector space V\, is the complex vector space \overline V consisting of all formal complex conjugates of elements of V\,...
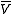 defined by
defined by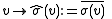 .
.Algebraic variety
For an algebraic varietyAlgebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
defined over a subfield of the real numbers,
the real structure is the complex conjugation acting on the points of the variety in complex projective or affine space.
Its fixed locus are the space of real points of the variety (which may be empty).
Scheme
For a scheme defined over a subfield of the real numbers, complex conjugationis in a natural way a member of the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of the algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of the basefield.
The real structure is the Galois action of this conjugation on the extension of the
scheme over the algebraic closure of the base field.
The real points are the points whose residue field is fixed (which may be empty).
See also
- Antilinear map
- Linear map
- Canonical complex conjugation map
- Complex conjugateComplex conjugateIn mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
- Complex conjugation
- Complex conjugate vector spaceComplex conjugate vector spaceIn mathematics, the complex conjugate of a complex vector space V\, is the complex vector space \overline V consisting of all formal complex conjugates of elements of V\,...
- Conjugate linear maps
- ComplexificationComplexificationIn mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
- Complex structure
- Linear complex structureLinear complex structureIn mathematics, a complex structure on a real vector space V is an automorphism of V that squares to the minus identity, −I. Such a structure on V allows one to define multiplication by complex scalars in a canonical fashion so as to regard V as a complex vector space.Complex structures have...
- Sesquilinear formSesquilinear formIn mathematics, a sesquilinear form on a complex vector space V is a map V × V → C that is linear in one argument and antilinear in the other. The name originates from the numerical prefix sesqui- meaning "one and a half"...
- Spinor calculus

