Regular extension
Encyclopedia
In field theory
, a branch of algebra, a field extension
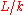is said to be regular if k is algebraically closed in L and L is separable
over k, or equivalently,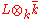
is an integral domain when 
is the algebraic closure of 
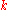(that is, to say, 
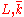are linearly disjoint
over k). In particular, any field extension of an algebraically closed field is regular. Also, a purely transcendental extension of a field is regular.
There is also a similar notion: a field extension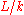
is said to be self-regular if 
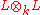is an integral domain. A self-regular extension is algebraically closed in k. However, a self-regular extension is not necessarily regular.
Field theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
, a branch of algebra, a field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
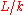is said to be regular if k is algebraically closed in L and L is separableSeparable extension
In modern algebra, an algebraic field extension E\supseteq F is a separable extension if and only if for every \alpha\in E, the minimal polynomial of \alpha over F is a separable polynomial . Otherwise, the extension is called inseparable...
over k, or equivalently,
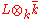is an integral domain when is the algebraic closure of 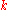(that is, to say, 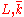are linearly disjointLinearly disjoint
In mathematics, algebras A, B over a field k inside some field extension \Omega of k are said to be linearly disjoint over k if the following equivalent conditions are met:...
over k). In particular, any field extension of an algebraically closed field is regular. Also, a purely transcendental extension of a field is regular.
There is also a similar notion: a field extension
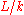is said to be self-regular if 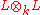is an integral domain. A self-regular extension is algebraically closed in k. However, a self-regular extension is not necessarily regular.