
Remez algorithm
Encyclopedia
The Remez algorithm published by Evgeny Yakovlevich Remez
in 1934 is an iterative algorithm used to find simple approximations to functions, specifically, approximations by functions in a Chebyshev space that are the best in the uniform norm L∞ sense.
A typical example of a Chebyshev space is the subspace of Chebyshev polynomials
of order n in the space
of real continuous function
s on an interval
, C[a, b].
The polynomial of best approximation within a given subspace is defined to be the one that minimizes the maximum absolute difference
between the polynomial and the function. In this case, the form of the solution is precised by the equioscillation theorem
.
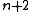 sample points
sample points 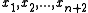 in the approximation interval, usually the Chebyshev nodes
in the approximation interval, usually the Chebyshev nodes
linearly mapped to the interval. The steps are:
The result is called the polynomial of best approximation, the Chebyshev approximation, or the minimax approximation.
A review of technicalities in implementing the Remez algorithm is given by W. Fraser.
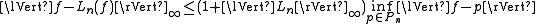
with the norm or Lebesgue constant
of the Lagrange interpolation operator Ln of the nodes (t1, ..., tn + 1) being
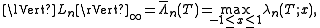
T being the zeros of the Chebyshev polynomials, and the Lebesgue functions being
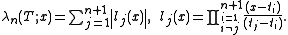
Theodore A. Kilgore, Carl de Boor, and Allan Pinkus proved that there exists a unique ti for each Ln, although not known explicitly for (ordinary) polynomials. Similarly,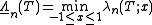 , and the optimality of a choice of nodes can be expressed as
, and the optimality of a choice of nodes can be expressed as 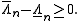
For Chebyshev nodes, which provides a suboptimal, but analytically explicit choice, the asymptotic behavior is known as
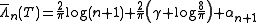
(γ being the Euler-Mascheroni constant
) with
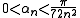 for
for 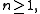
and upper bound
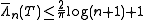
Lev Brutman obtained the bound for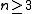 , and
, and 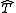 being the zeros of the expanded Chebyshev polynomials:
being the zeros of the expanded Chebyshev polynomials:
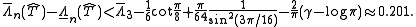
Rüdiger Günttner obtained from a sharper estimate for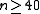
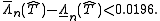
Sometimes relative error is used to measure the difference between the approximation and the function, especially if the approximation will be used to compute the function on a computer which uses floating point
arithmetic.
Evgeny Yakovlevich Remez
Evgeny Yakovlevich Remez Evgeny Yakovlevich Remez Evgeny Yakovlevich Remez (sometimes spelled as Evgenii Yakovlevich Remez, ; (born 1896 in Mstislavl, now Belarus; died 1975 in Kiev) was a Soviet mathematician...
in 1934 is an iterative algorithm used to find simple approximations to functions, specifically, approximations by functions in a Chebyshev space that are the best in the uniform norm L∞ sense.
A typical example of a Chebyshev space is the subspace of Chebyshev polynomials
Chebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
of order n in the space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of real continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s on an interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
, C[a, b].
The polynomial of best approximation within a given subspace is defined to be the one that minimizes the maximum absolute difference
Absolute difference
The absolute difference of two real numbers x, y is given by |x − y|, the absolute value of their difference. It describes the distance on the real line between the points corresponding to x and y...
between the polynomial and the function. In this case, the form of the solution is precised by the equioscillation theorem
Equioscillation theorem
The equioscillation theorem concerns the approximation of continuous functions using polynomials when the merit function is the maximum difference . Its discovery is attributed to Chebyshev.- Statement :...
.
Procedure
The Remez algorithm starts with the function f to be approximated and a set X of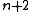 sample points
sample points 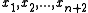 in the approximation interval, usually the Chebyshev nodes
in the approximation interval, usually the Chebyshev nodesChebyshev nodes
In numerical analysis, Chebyshev nodes are the roots of the Chebyshev polynomial of the first kind. They are often used as nodes in polynomial interpolation because the resulting interpolation polynomial minimizes the Runge's phenomenon.-Definition:...
linearly mapped to the interval. The steps are:
- Solve the linear system of equations
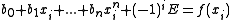 (where
(where 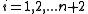 ),
),
- for the unknowns
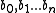 and E.
and E.
- Use the
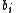 as coefficients to form a polynomial
as coefficients to form a polynomial 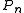 .
. - Find the set M of points of local maximum error
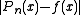 .
. - If the errors at every
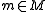 are of equal magnitude and alternate in sign, then
are of equal magnitude and alternate in sign, then 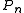 is the minimax approximation polynomial. If not, replace X with M and repeat the steps above.
is the minimax approximation polynomial. If not, replace X with M and repeat the steps above.
- Use the
The result is called the polynomial of best approximation, the Chebyshev approximation, or the minimax approximation.
A review of technicalities in implementing the Remez algorithm is given by W. Fraser.
On the choice of initialization
The Chebyshev nodes are a common choice for the initial approximation because of their role in the theory of polynomial interpolation. For the initialization of the optimization problem for function f by the Lagrange interpolant Ln(f), it can be shown that this initial approximation is bounded by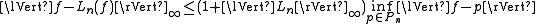
with the norm or Lebesgue constant
Lebesgue constant (interpolation)
In mathematics, the Lebesgue constants give an idea of how good the interpolant of a function is in comparison with the best polynomial approximation of the function...
of the Lagrange interpolation operator Ln of the nodes (t1, ..., tn + 1) being
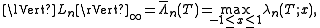
T being the zeros of the Chebyshev polynomials, and the Lebesgue functions being
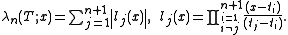
Theodore A. Kilgore, Carl de Boor, and Allan Pinkus proved that there exists a unique ti for each Ln, although not known explicitly for (ordinary) polynomials. Similarly,
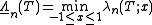 , and the optimality of a choice of nodes can be expressed as
, and the optimality of a choice of nodes can be expressed as 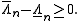
For Chebyshev nodes, which provides a suboptimal, but analytically explicit choice, the asymptotic behavior is known as
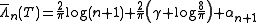
(γ being the Euler-Mascheroni constant
Euler-Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
) with
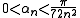 for
for 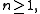
and upper bound
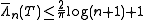
Lev Brutman obtained the bound for
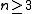 , and
, and 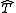 being the zeros of the expanded Chebyshev polynomials:
being the zeros of the expanded Chebyshev polynomials: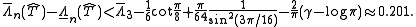
Rüdiger Günttner obtained from a sharper estimate for
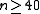
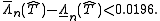
Variants
Sometimes more than one sample point is replaced at the same time with the locations of nearby maximum absolute differences.Sometimes relative error is used to measure the difference between the approximation and the function, especially if the approximation will be used to compute the function on a computer which uses floating point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
arithmetic.

