Representation theory of diffeomorphism groups
Encyclopedia
In mathematics
, a source for the representation theory
of the group
of diffeomorphism
s of a smooth manifold M is the initial observation that (for M connected) that group acts transitively on M.
, Israel Gelfand
and M. I. Graev attributes the original interest in the topic to research in theoretical physics
of the local current algebra, in the preceding years. Research on the finite configuration representations was in papers of R. S. Ismagilov (1971), and A. A. Kirillov (1974). The representations of interest in physics are described as a cross product C∞(M)·Diff(M).
differentiable manifold
, and x be any point on it. Let Diff(M) be the orientation-preserving diffeomorphism group of M (only the identity component
of mappings homotopic to the identity diffeomorphism if you wish) and Diffx1(M) the stabilizer of x. Then, M is identified as a homogeneous space
From the algebraic point of view instead,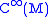
is the algebra
of smooth function
s over M and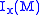
is the ideal
of smooth functions vanishing at x. Let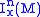
be the ideal of smooth functions which vanish up to the n-1th partial derivative
at x.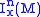
is invariant under the group Diffx1(M) of diffeomorphisms fixing x. For n > 0 the group Diffxn(M) is defined as the subgroup
of Diffx1(M) which acts as the identity on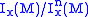
. So, we have a descending chain
Here Diffxn(M) is a normal subgroup
of Diffx1(M), which means we can look at the quotient group
Using harmonic analysis
, a real- or complex-valued function (with some sufficiently nice topological properties) on the diffeomorphism group can be decomposed into Diffx1(M) representation-valued functions over M.
φ:G → H, then if we have a H-representation, we can obtain a restricted G-representation. So, if we have a rep of
we can obtain a rep of Diffx1(M).
Let's look at
first. This is isomorphic to the general linear group
GL+(n, R) (and because we're only considering orientation preserving diffeomorphisms and so the determinant is positive). What are the reps of GL+(n, R)?
.
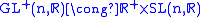We know the reps of SL(n, R) are simply tensor
s over n dimensions. How about the R+ part? That corresponds to the density, or in other words, how the tensor rescales under the determinant
of the Jacobian
of the diffeomorphism at x. (Think of it as the conformal weight if you will, except that there is no conformal structure here). (Incidentally, there is nothing preventing us from having a complex density).
So, we have just discovered the tensor reps (with density) of the diffeomorphism group.
Let's look at
This is a finite-dimensional group. We have the chain
Here, the "⊂" signs should really be read to mean an injective homomorphism, but since it is canonical, we can pretend these quotient groups are embedded one within the other.
Any rep of
can automatically be turned into a rep of
if n > m. Let's say we have a rep of
which doesn't arise from a rep of
Then, we call the fiber bundle
with that rep as the fiber
(i.e. Diffx1/Diffxp + 2 is the structure group) a jet bundle
of order p.
Side remark: This is really the method of induced representation
s with the smaller group being Diffx1(M) and the larger group being Diff(M).
If the fiber is not an irreducible representation of Diffx1(M), then we can have a nonzero intertwiner mapping each fiber pointwise into a smaller quotient representation. Also, the exterior derivative
is an intertwiner from the space of differential form
s to another of higher order. (Other derivatives are not, because connections
aren't invariant under diffeomorphisms, though they are covariant.) The partial derivative
isn't diffeomorphism invariant. There is a derivative intertwiner taking sections of a jet bundle of order p into sections of a jet bundle of order p + 1.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a source for the representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s of a smooth manifold M is the initial observation that (for M connected) that group acts transitively on M.
History
A survey paper from 1975 of the subject by Anatoly VershikAnatoly Vershik
Anatoly Moiseevich Vershik is a Soviet and Russian mathematician. He is most famous for his joint work with Sergey V. Kerov on representations of infinite symmetric groups and applications to the longest increasing subsequences....
, Israel Gelfand
Israel Gelfand
Israel Moiseevich Gelfand, also written Israïl Moyseyovich Gel'fand, or Izrail M. Gelfand was a Soviet mathematician who made major contributions to many branches of mathematics, including group theory, representation theory and functional analysis...
and M. I. Graev attributes the original interest in the topic to research in theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
of the local current algebra, in the preceding years. Research on the finite configuration representations was in papers of R. S. Ismagilov (1971), and A. A. Kirillov (1974). The representations of interest in physics are described as a cross product C∞(M)·Diff(M).
Constructions
Let therefore M be a n-dimensional connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
, and x be any point on it. Let Diff(M) be the orientation-preserving diffeomorphism group of M (only the identity component
Identity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
of mappings homotopic to the identity diffeomorphism if you wish) and Diffx1(M) the stabilizer of x. Then, M is identified as a homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
- Diff(M)/Diffx1(M).
From the algebraic point of view instead,
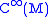is the algebraAssociative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
of smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s over M and
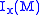is the idealIdeal
-In philosophy:* Ideal , values that one actively pursues as goals* Platonic ideal, a philosophical idea of trueness of form, associated with Plato-In mathematics:* Ideal , special subsets of a ring considered in abstract algebra...
of smooth functions vanishing at x. Let
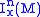be the ideal of smooth functions which vanish up to the n-1th partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
at x.
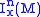is invariant under the group Diffx1(M) of diffeomorphisms fixing x. For n > 0 the group Diffxn(M) is defined as the subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of Diffx1(M) which acts as the identity on
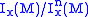. So, we have a descending chain- Diff(M) ⊃ Diffx1(M) ⊃ ... ⊃ Diffxn(M) ⊃ ...
Here Diffxn(M) is a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of Diffx1(M), which means we can look at the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
- Diffx1(M)/Diffxn(M).
Using harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
, a real- or complex-valued function (with some sufficiently nice topological properties) on the diffeomorphism group can be decomposed into Diffx1(M) representation-valued functions over M.
The supply of representations
So what are the reps of Diffx1(M)? Let's use the fact that if we have a group homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
φ:G → H, then if we have a H-representation, we can obtain a restricted G-representation. So, if we have a rep of
- Diffx1(M)/Diffxn(M),
we can obtain a rep of Diffx1(M).
Let's look at
- Diffx1(M)/Diffx2(M)
first. This is isomorphic to the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL+(n, R) (and because we're only considering orientation preserving diffeomorphisms and so the determinant is positive). What are the reps of GL+(n, R)?
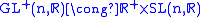.We know the reps of SL(n, R) are simply tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s over n dimensions. How about the R+ part? That corresponds to the density, or in other words, how the tensor rescales under the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the Jacobian
Jacobian
In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
of the diffeomorphism at x. (Think of it as the conformal weight if you will, except that there is no conformal structure here). (Incidentally, there is nothing preventing us from having a complex density).
So, we have just discovered the tensor reps (with density) of the diffeomorphism group.
Let's look at
- Diffx1(M)/Diffxn(M).
This is a finite-dimensional group. We have the chain
- Diffx1(M)/Diffx1(M) ⊂ ... ⊂ Diffx1(M)/Diffxn(M) ⊂ ...
Here, the "⊂" signs should really be read to mean an injective homomorphism, but since it is canonical, we can pretend these quotient groups are embedded one within the other.
Any rep of
- Diffx1(M)/Diffxm(M)
can automatically be turned into a rep of
- Diffx1/Diffxn(M)
if n > m. Let's say we have a rep of
- Diffx1/Diffxp + 2
which doesn't arise from a rep of
- Diffx1/Diffxp + 1.
Then, we call the fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
with that rep as the fiber
Fiber
Fiber is a class of materials that are continuous filaments or are in discrete elongated pieces, similar to lengths of thread.They are very important in the biology of both plants and animals, for holding tissues together....
(i.e. Diffx1/Diffxp + 2 is the structure group) a jet bundle
Jet bundle
In differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form...
of order p.
Side remark: This is really the method of induced representation
Induced representation
In mathematics, and in particular group representation theory, the induced representation is one of the major general operations for passing from a representation of a subgroup H to a representation of the group G itself. It was initially defined as a construction by Frobenius, for linear...
s with the smaller group being Diffx1(M) and the larger group being Diff(M).
Intertwining structure
In general, the space of sections of the tensor and jet bundles would be an irreducible representation and we often look at a subrepresentation of them. We can study the structure of these reps through the study of the intertwiners between them.If the fiber is not an irreducible representation of Diffx1(M), then we can have a nonzero intertwiner mapping each fiber pointwise into a smaller quotient representation. Also, the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
is an intertwiner from the space of differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s to another of higher order. (Other derivatives are not, because connections
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
aren't invariant under diffeomorphisms, though they are covariant.) The partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
isn't diffeomorphism invariant. There is a derivative intertwiner taking sections of a jet bundle of order p into sections of a jet bundle of order p + 1.